Quantenzustand

Ein Zustand beschreibt in der Quantenphysik ein Teilchen oder ein Mehrteilchensystem. Während in der klassischen Mechanik der Zustand eines Teilchens durch seinen Ort und seinen Impuls (d. h. durch die Position im kontinuierlichen Phasenraum) gegeben ist, werden die Zustände eines quantenmechanischen Systems durch Quantenzahlen, oder als Superposition von Zuständen mit bekannten Quantenzahlen beschrieben.

Notation

Die Angaben, die den Zustand beschreiben, werden in spitze Klammern (engl. brackets, daher bra und ket) geschrieben. Die ket-Zustände sind dann z. B. | ψ > , wohingegen ihre adjungierten Gegenstücke als bra notiert werden < ψ | .

Ist der Zustand ein Eigenzustand eines hermiteschen Operators, so werden die Eigenwerte (=Quantenzahlen) in diese Klammern gesetzt: $|n&amp;gt;, |j, m&amp;gt;, |\uparrow&amp;gt;$.

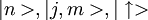Da unter den Zuständen Vektoren in einem Hilbertraum zu verstehen sind, nennt man die kets auch Spaltenvektoren, die bras Zeilenvektoren, zwischen denen man auch ein Skalarprodukt bilden, oder das Matrixelement eines Operators berechnen kann: < φ | ψ > , bzw. < φ | Operator | ψ > .

Beispiele

a) Die Zustände eines Teilchens in einem Potentialtopf der Breite a (von 0 bis a) sind Superpositionen von Eigenzuständen des Energieoperators, die durch die Wellenfunktionen 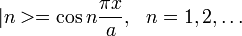$|n&amp;gt; = \cos n\frac{\pi x}{a},\ \ n=1,2,\dots$ beschrieben sind und die Energieeigenwerte 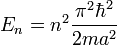$E_n = n^2 \frac{\pi^2 \hbar^2}{2 m a^2}$ haben. Ein allgemeiner Zustand lässt sich dann immer als 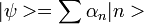$|\psi&amp;gt; = \sum \alpha_n |n&amp;gt;$ schreiben.

b) Für Teilchen in einem Zentralfeld sind die Eigenzustände des Drehimpulsoperators durch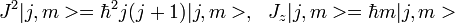

$J^2 |j,m&amp;gt; = \hbar^2 j (j+1) |j,m&amp;gt;,\ \ J_z |j,m&amp;gt; = \hbar m |j,m&amp;gt;$

gegeben, so dass ein allgemeiner Zustand als 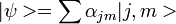$|\psi&amp;gt; = \sum \alpha_{jm} |j,m&amp;gt;$ geschrieben werden kann.

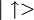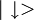c) Die Spineigenzustände eines (fermionischen) Teilchens werden einfach als $|\uparrow&amp;gt;$ und $|\downarrow&amp;gt;$ geschrieben.

Allgemeines

Im mathematischen Formalismus der Quantenmechanik und Quantenfeldtheorie ist ein Zustand ein abstraktes Objekt. Der Bezug eines Zustandes zur realen Welt wird durch spezielle Darstellungen beispielsweise in Ortskoordinaten oder Impulskoordinaten repräsentiert. Die Darstellung in Ortskoordinaten wird häufig als Wellenfunktion bezeichnet. Aus diesen Darstellungen der Zustandsvektoren lassen sich nach den Gesetzen der Quantenmechanik exakte Wahrscheinlichkeitsaussagen über Eigenschaften von Teilchen oder Teilchensystemen machen. Die zeitliche Veränderung der Zustandsvektoren wird in der Quantenmechanik durch die Schrödingergleichung beschrieben und ist damit eindeutig bestimmt.

Meist ist mit einem Zustand ein Element (Vektor) eines abstrakten Hilbertraums gemeint. Zustände, die auf diese Weise dargestellt werden, heißen Vektorzustände. Die meisten Zustände lassen sich jedoch nur über Dichtematrizen oder gar nicht in einem Hilbertraum darstellen. Zur Beschreibung allgemeiner Zustände wird der Formalismus der C*-Algebren herangezogen.

Siehe auch

• Mathematische Struktur der Quantenmechanik
• Quantenmechanische Messung