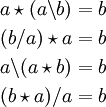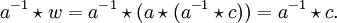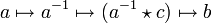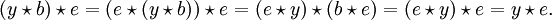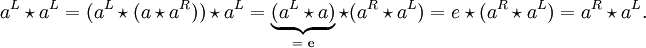- Quasi-Gruppe
-
In der Mathematik ist eine Quasigruppe eine nichtleere Menge Q mit einer binären Verknüpfung
 , in der für alle a und b in Q die Gleichungen
, in der für alle a und b in Q die Gleichungenund
jeweils genau eine Lösung haben, d.h., die Lösung existiert und ist eindeutig.
Eine Quasigruppe ist von Strukturen zu unterscheiden, in denen lediglich die sog. Kürzungseigenschaft (s. u.) gefordert wird. Dort wird zwar auch die Eindeutigkeit der Lösungen dieser Gleichungen gefordert, aber nur falls überhaupt eine Lösung existiert. Auf die Nichtleerheit der zugrundegelegten Menge kann auch verzichtet werden, dann ist die leere Menge trivialerweise auch eine Quasigruppe.
Eine Quasigruppe ist ein Spezialfall eines Magmas. Ein Magma ist genau dann eine Quasigruppe, wenn die Verknüpfungstabelle ein Lateinisches Quadrat ist, wenn also in jeder Zeile und in jeder Spalte der Tabelle jedes Element von Q genau einmal vorkommt.
Inhaltsverzeichnis
Beispiele
Jede Gruppe ist eine Quasigruppe, denn
 ist genau für
ist genau für 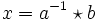 und
und 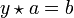 genau für
genau für 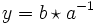 erfüllt.
erfüllt.Jeder Vektorraum über einem Körper der Charakteristik ungleich 2 ist eine Quasigruppe mit der Verknüpfung
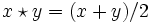 .
.Jedes Steinersche Tripel-System ist eine Quasigruppe.
Jede Menge von Nichtnull-Elementen in einer nullteilerfreien endlichdimensionalen Algebra ist eine Quasigruppe (z. B. die Oktaven ohne 0).
Die einzige Quasigruppe der Ordnung 2 ist die zyklische Gruppe
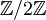 . Es gibt fünf Quasigruppen der Ordnung 3, von denen nur Eine eine Gruppe ist. Die kleinste echte Loop (die nicht assoziativ ist) hat die Ordnung 5.
. Es gibt fünf Quasigruppen der Ordnung 3, von denen nur Eine eine Gruppe ist. Die kleinste echte Loop (die nicht assoziativ ist) hat die Ordnung 5.Wie viele Probleme der Gruppentheorie finden auch Quasigruppen wichtige Anwendungen im Bereich der Kryptographie. Es lassen sich Hashfunktionen, Blockchiffren und auch Signaturverfahren konstruieren (siehe externe Links).
Eigenschaften
Jede Quasigruppe hat die Kürzungseigenschaft, d.h.
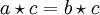 folgt a = b
folgt a = b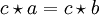 folgt a = b
folgt a = b
Das liegt daran, dass die linken Gleichungen bedeuten, dass x1 = a und x2 = b Lösungen der Gleichung
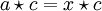 (bzw.
(bzw.  ) sind. Weil in einer Quasigruppe aber höchstens eine Lösung für die Gleichung existiert, folgt x1 = x2 bzw. a = b.
) sind. Weil in einer Quasigruppe aber höchstens eine Lösung für die Gleichung existiert, folgt x1 = x2 bzw. a = b.Anders ausgedrückt besagt die Kürzungseigenschaft nichts anderes, als dass sowohl die Links- als auch die Rechtsmultiplikation mit einem Element a aus Q eine injektive Abbildung von Q in sich beschreiben
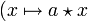 bzw.
bzw. 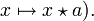 Da Injektivität und Surjektivität für endliche Mengen identisch sind, sind die beiden Abbildungen für endliches Q ersichtlich bijektiv. Aber auch im allgemeinen Fall (d. h. inklusive unendlichem Q) ergibt sich die Bijektivität, da die Surjektivität durch die Existenz der Lösung jeder Gleichung
Da Injektivität und Surjektivität für endliche Mengen identisch sind, sind die beiden Abbildungen für endliches Q ersichtlich bijektiv. Aber auch im allgemeinen Fall (d. h. inklusive unendlichem Q) ergibt sich die Bijektivität, da die Surjektivität durch die Existenz der Lösung jeder Gleichung 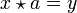 bzw.
bzw. 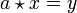 garantiert wird. Denn damit gibt es zu jedem Bild y einer Links- oder Rechtsmultiplikation mit dem Element a ein Urbild x.
garantiert wird. Denn damit gibt es zu jedem Bild y einer Links- oder Rechtsmultiplikation mit dem Element a ein Urbild x.Die Bijektivität dieser beiden Abbildungen ist eine definierende Eigenschaft der Quasigruppen, d.h. sie kann ohne Weiteres zur alternativen Definition der Quasigruppen herangezogen werden: Ein Magma ist genau dann eine Quasigruppe, wenn in ihm die durch die Rechts- und Linksmultiplikation induzierten Abbildungen bijektiv sind. Die Surjektivität garantiert dabei die Existenz der Lösungen der Gleichungen (1) und (2), aus der Injektivität ergibt sich die Eindeutigkeit.
Viele Beweise aus der Gruppentheorie, zu Aussagen, die sich speziell auf Gruppen beziehen, benutzen ganz wesentlich diese Eigenschaft. Benutzen sie nur diese Eigenschaft (von allen Eigenschaften, die sich rein aus den Gruppenaxiomen ergeben), so können die gemachten Aussagen sofort auf Quasigruppen verallgemeinert werden. Aber auch viele Aussagen, die nur geringfügig stärkere Voraussetzungen machen, können auf spezielle Quasigruppen – die keine Gruppen sein müssen – verallgemeinert werden.
Die Verknüpfungstabelle einer endlichen Quasigruppe ist ein lateinisches Quadrat: Eine
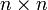 -Tabelle gefüllt mit n verschiedenen Symbolen, in der in jeder Zeile und in jeder Spalte jedes Symbol genau einmal vorkommt. Umgekehrt ist jedes lateinische Quadrat Verknüpfungstabelle einer Quasigruppe. Damit sind lateinische Quadrate und die hier ausgeführte abstrakt-beschreibende Definition lediglich zwei unterschiedliche, prinzipiell gleichberechtigte Darstellungen desselben mathematischen Objektes Quasigruppe.
-Tabelle gefüllt mit n verschiedenen Symbolen, in der in jeder Zeile und in jeder Spalte jedes Symbol genau einmal vorkommt. Umgekehrt ist jedes lateinische Quadrat Verknüpfungstabelle einer Quasigruppe. Damit sind lateinische Quadrate und die hier ausgeführte abstrakt-beschreibende Definition lediglich zwei unterschiedliche, prinzipiell gleichberechtigte Darstellungen desselben mathematischen Objektes Quasigruppe.Alternative Definition
Man kann in einer Quasigruppe Q zwei weitere Verknüpfungen definieren: Für a und b aus Q sei
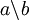 die Lösung von
die Lösung von  und sei
und sei 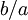 die Lösung von
die Lösung von 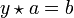 (man kann sich diese beiden als „Quasi-Brüche“ bzw. Links- und Rechtsbrüche „b links-durch a“ und „b rechts-durch a“ denken). Dann gilt offenbar:
(man kann sich diese beiden als „Quasi-Brüche“ bzw. Links- und Rechtsbrüche „b links-durch a“ und „b rechts-durch a“ denken). Dann gilt offenbar:Dabei beschreiben die ersten beiden Gleichungen die Lösbarkeit von (1) und (2), und die anderen beiden Gleichungen die Eindeutigkeit der Lösungen. Man kann eine Quasigruppe also auch definieren als Algebra
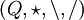 mit drei binären Verknüpfungen, die die eben genannten vier Gleichungen erfüllen.
mit drei binären Verknüpfungen, die die eben genannten vier Gleichungen erfüllen.Ist Q eine Gruppe, dann ist
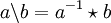 und
und 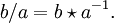 Ist die Quasigruppe kommutativ, dann sind die beiden Forderungen nach der eindeutigen Lösbarkeit von (1) und (2) gleichwertig und die Verknüpfungen
Ist die Quasigruppe kommutativ, dann sind die beiden Forderungen nach der eindeutigen Lösbarkeit von (1) und (2) gleichwertig und die Verknüpfungen 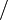 und
und 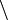 fallen zusammen.
fallen zusammen.Weitere alternative Definitionen sind z. B. die unter Eigenschaften beschriebene Definition einer Quasigruppe als Magma, in dem die Links- und Rechtsmultiplikation bijektive Abbildungen induzieren. Aber auch eine andere, zur anfänglich gemachten Definition nur leicht abgewandelte Form, kann schon eine etwas andere Sicht auf Quasigruppen erreichen: Eine Quasigruppe Q ist ein Magma (Menge mit zweistelliger innerer Verknüpfung), in der in jeder Gleichung der Form
 je zwei Elemente (aus Q), die Existenz des Dritten (in Q) bedingen und eindeutig bestimmen. Diese Definition ist zwar etwas redundant, da sich Existenz und Eindeutigkeit von c schon aus der Definition der inneren Verknüpfung ergeben, sie beschreibt jedoch gleichberechtigter und unmittelbarer die Beziehungen der Elemente untereinander.
je zwei Elemente (aus Q), die Existenz des Dritten (in Q) bedingen und eindeutig bestimmen. Diese Definition ist zwar etwas redundant, da sich Existenz und Eindeutigkeit von c schon aus der Definition der inneren Verknüpfung ergeben, sie beschreibt jedoch gleichberechtigter und unmittelbarer die Beziehungen der Elemente untereinander.Quasigruppe mit Inverseneigenschaft
Eine Quasigruppe mit Inverseneigenschaft ist ein Magma Q, in dem es für alle a und b aus Q ein eindeutiges Element a − 1 gibt, so dass gilt:
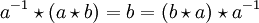 (Inverseneigenschaft).
(Inverseneigenschaft).
Wie der Name anzeigt, ist eine Quasigruppe mit Inverseneigenschaft eine Quasigruppe, was wir hier beweisen wollen. Wir zeigen zunächst, dass eine Lösung x der Gleichung
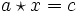 mit a und c aus Q existiert; die Existenz von x für
mit a und c aus Q existiert; die Existenz von x für 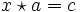 folgt analog. Sei dazu
folgt analog. Sei dazu 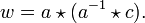 Dann folgt aus der linken Seite der Inversengleichung:
Dann folgt aus der linken Seite der Inversengleichung:Multiplikation von links mit (a − 1) − 1 gibt
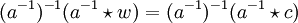 also w = c. Das bedeutet aber
also w = c. Das bedeutet aber 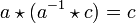 , womit
, womit 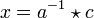 eine Lösung der Gleichung
eine Lösung der Gleichung 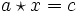 ist.
ist.Die Eindeutigkeit der Lösung b (und analog der Lösung a) folgt weil
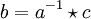 nur von a und c abhängt und die Zuordnung
nur von a und c abhängt und die Zuordnungin jedem Teilschritt eindeutig ist.
Loop
Hat eine Quasigruppe ein neutrales Element, dann heißt sie eine Loop. Direkt aus der Definition der Quasigruppe folgt, dass in einer Loop jedes Element ein linksinverses und ein rechtsinverses Element hat[1], die aber – im Gegensatz zur Situation in einer Gruppe – nicht übereinstimmen müssen (siehe auch inverses Element). Die Struktur von Loops ist denen von Gruppen sehr ähnlich.
Eine Moufang-Loop (benannt nach Ruth Moufang) ist eine Quasigruppe Q, in der für alle a,b und c aus Q gilt:
Wie der Name anzeigt, ist eine Moufang-Loop eine Loop, was wir hier beweisen wollen. Sei a ein Element von Q und
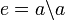 das (eindeutig bestimmte) Element mit
das (eindeutig bestimmte) Element mit 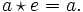 Dann gilt für jedes x in Q:
Dann gilt für jedes x in Q:also nach dem Kürzen
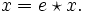 Damit ist e ein linksneutrales Element. Sei nun
Damit ist e ein linksneutrales Element. Sei nun  das (eindeutig bestimmte) Element mit
das (eindeutig bestimmte) Element mit  Dann gilt
Dann gilt 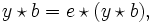 da e linksneutral ist, und
da e linksneutral ist, undKürzen von e ergibt
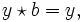 also ist b ein rechtsneutrales Element. Schließlich erhalten wir
also ist b ein rechtsneutrales Element. Schließlich erhalten wir 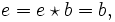 also ist e ein beidseitig neutrales Element.
also ist e ein beidseitig neutrales Element.Da in einer Loop Links- und Rechtsinverse existieren, zeigt man analog, dass diese in einer Moufang-Loop identisch sind: Zu a aus Q seien aL und aR Links- und Rechsinverses. Dann gilt insbesondere
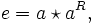 da aR rechtsneutral ist, und dann
da aR rechtsneutral ist, und dann 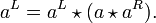 Multiplikation von rechts mit aL gibt:
Multiplikation von rechts mit aL gibt:Kürzen von aL ergibt aL = aR.
Jede assoziative Quasigruppe ist eine Moufang-Loop, und als assoziative Loop folglich eine Gruppe (da die Gruppenaxiome dann offensichtlich erfüllt sind). Dies zeigt, dass die Gruppen genau die assoziativen Quasigruppen sind (bzw. jene Quasigruppen, die gleichzeitig auch Halbgruppen sind).
Literatur
- Hall, Marshall: The theory of groups. © Macmillan New York, 1959.
- Kurosch, Aleksander Gennadljewitsch: Gruppentheorie.
Weblinks
- Enthält auch Verknüpfungstabellen der Quasigruppen der Ordnung 3 und einer echten Loop der Ordnung 5.
- Hashverfahren auf Basis Quasigruppen String Transformationen
- Übersicht über die wichtigsten kryptographische Anwendungen der Quasigruppen
Einzelnachweise/Fußnoten
- ↑ Nämlich die Lösungen der Gleichungen
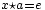 und
und 
- ↑ Wenn man für die Reihenfolge des Ausrechnens der Verknüpfungen „von Links nach Rechts“ als Standard annimmt und solche Klammern, die diese Reihenfolge ergeben, weglässt, sieht man besser, was gemeint ist:
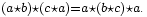 Informell ausgedrückt: Man kann erst die beiden äußeren Paare ausrechnen und dann „normal“ (von Links nach Rechts) weiterrechnen, oder erst „die Mitte“ ausrechnen und dann „normal“ weitermachen – beides führt zum selben Ergebnis.
Informell ausgedrückt: Man kann erst die beiden äußeren Paare ausrechnen und dann „normal“ (von Links nach Rechts) weiterrechnen, oder erst „die Mitte“ ausrechnen und dann „normal“ weitermachen – beides führt zum selben Ergebnis.
Wikimedia Foundation.