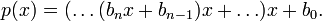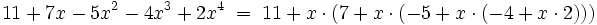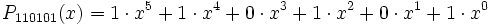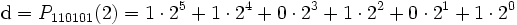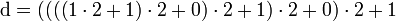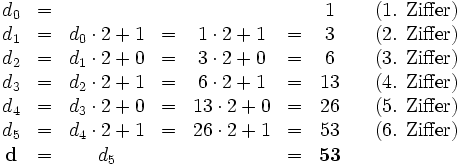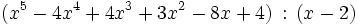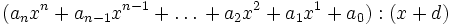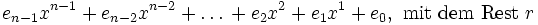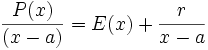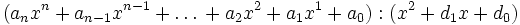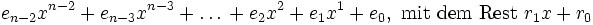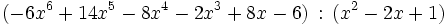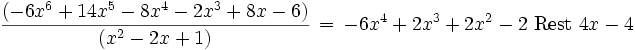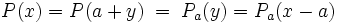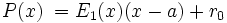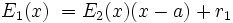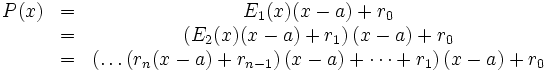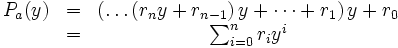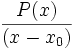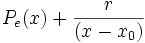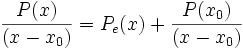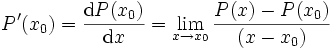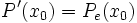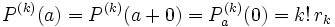- Regel von Ruffini
-
Das Horner-Schema (nach William George Horner) ist ein Umformungsverfahren für Polynome, um die Berechnung von Funktionswerten zu erleichtern. Es kann genutzt werden, um die Polynomdivision sowie die Berechnung von Nullstellen und Ableitungen zu vereinfachen.
Definition
Zu einem Polynom
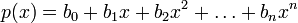 vom Grade n aus einem beliebigen Polynomring ist das Horner-Schema definiert als:
vom Grade n aus einem beliebigen Polynomring ist das Horner-Schema definiert als:Funktion des Hornerschemas
Rechenvorteile
Bei Polynomen in der klassischen Schreibweise müssen die Potenzen a2, a3 usw. errechnet werden, wenn der Funktionswert an einer Stelle x = a errechnet werden soll. Im umgeformten Polynom nach dem Horner-Schema kommen keine Potenzen, sondern nur noch Multiplikation und Addition vor. Die Berechnung wird beschleunigt, weil weniger Multiplikationen nötig sind: Deren Anzahl wird durch die Anwendung des Horner-Schemas auf fast die Hälfte reduziert.
Erfolgt die Auswertung durch Gleitkommaoperationen, so wird darüber hinaus auch der Rechenfehler geringer gehalten.
Verfahren
Durch fortgesetztes Ausklammern der freien Polynomvariablen x wird das Polynom als Schachtelung von Produkten und Summen dargestellt.
Beispiel
Das folgende Beispiel illustriert den geringeren Rechenaufwand beim Hornerschema:
In der klassischen Darstellung (linke Seite) werden 7 Multiplikationen benötigt, davon 3 zur Bildung der Potenzen a2, a3, a4. Im Horner-Schema (rechte Seite) kommt man dagegen mit 4 Multiplikationen aus. Die Zahl der – rechnerisch weniger aufwendigen – Additionen ist in beiden Fällen gleich, nämlich 4.
Anwendung
In der Analysis müssen häufig die Werte eines Polynoms und seiner Ableitung berechnet werden: Sei es, um eine Nullstelle zu bestimmen, eine Kurvendiskussion durchzuführen oder um einen Graphen zu skizzieren.
Die hier dargestellte Form eignet sich besonders gut für die Berechnung in der umgekehrten polnischen Notation (UPN).
Tabellarische Schreibweise des Hornerschemas
Betrachten wir nochmals obiges Beispiel und setzen:
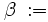
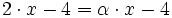
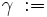
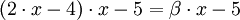
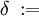
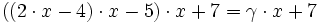
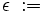
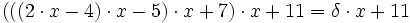
Nun überträgt man die Koeffizienten, die Zwischenprodukte und Teilsummen in eine 3zeilige-Tabelle, wobei in die erste Zeile die Koeffizienten eingetragen werden. In die dritte Zeile kommen die Teilsummen. Dabei wird der erste Koeffizient des Polynoms direkt übernommen. Die zuvor berechnete Teilsumme multipliziert mit x ergibt dann den nächsten Summanden, den man dann in die zweite Zeile unter den folgenden Koeffizienten einträgt.
So erhält man nach und nach das folgende Rechenschema:
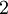
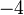
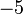
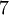
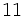
+ + + + 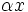
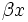
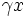
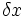
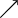
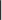
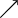
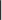
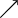
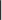
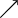
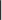
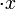
= 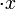
= 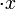
= 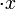
= 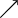
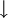
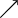
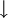
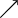
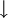
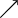
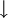
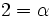
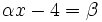
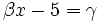
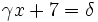
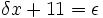
Beispiel
Die Berechnung des obigen Polynoms für x = 2 mit Hilfe des Horner-Schemas stellt sich wie folgt dar:
2 −4 −5 7 11 2 ) 4 0 −10 −6 2 0 −5 −3 5 Den Wert, für den man das Polynom berechnen möchte, schreibt man dabei üblicherweise in die zweite Zeile vor das Schema. Anschließend multipliziert man die erste Zahl im Schema mit diesem Wert und addiert das Ergebnis zur ersten Zeile (letzte Zeile). Multiplikation dieses Ergebniswertes in der letzten Zeile mit dem Wert, für den man das Polynom berechnen möchte, liefert jeweils den folgenden Ergebniswert. Die letzte Zahl (hier fünf) ist das Endergebnis.
Anwendungsmöglichkeiten des Hornerschemas
Umwandlung zwischen verschiedenen Zahlensystemen
Unsere vertraute Darstellung von Zahlen im dezimalen Stellenwertsystem ist nichts anderes als eine verkürzte Schreibweise für besondere Polynome, nämlich Polynome mit der Basis x = 10. Das gleiche gilt für alle anderen Stellenwertsysteme, beispielsweise das Binärsystem. Dort ist x = 2. Wir können uns das Horner-Schema zunutze machen, um Zahlen aus jedem anderen Stellenwertsystem in das Dezimalsystem umzuwandeln, und umgekehrt.
Umwandlung ins Dezimalsystem
Beispiel: Die Binärzahl 110101 soll in das Dezimalsystem umgewandelt werden. Wie lautet die sich ergebende Dezimalzahl d?
Wir schreiben 110101binär als Polynom:
so ist
Nach dem Horner-Schema:
Wir brauchen das nun nicht in einem Zuge auszurechnen, sondern können schrittweise vorgehen. Jeder Schritt besteht aus einer Multiplikation mit 2 und einer Addition. Der Übersicht halber schreiben wir die Schritte untereinander und notieren die Zwischenergebnisse:
Wir haben unsere gesuchte Dezimaldarstellung gefunden.
Verallgemeinert lautet das Verfahren: Eine Zahl aus einem Stellenwertsystem zur Basis x wird in das Dezimalsystem umgewandelt, indem
- der Wert der ersten Ziffer als Anfangswert genommen wird
- danach schrittweise das Ergebnis aus dem vorigen Schritt mit x multipliziert und die nächste Ziffer addiert wird
- bis alle Ziffern aufgebraucht sind.
Am einfachsten schreibt man die Rechnung wieder in tabellarischer Form auf:
1 1 0 1 0 1 2 ) 2 6 12 26 52 1 3 6 13 26 53 kaskadiertes Horner-Schema
Der Nachteil des einstufigen Horner-Schemas besteht darin, dass Multiplikationen mit großen Faktoren nötig werden können (im obigen Beispiel 2*26 = 52). Um innerhalb des kleinen Einmaleins zu bleiben, wendet man das kaskadierte oder mehrstufige Horner-Schema an.
Dabei wird nur der Einer für die Multiplikation herangezogen. Der Zehner wird wie ein Übertrag in die nächste Zeile unter den Einer geschrieben. Bei der 13 aus dem obigen Beispiel wird also die 3 unter die 12 geschrieben und die 1 unter die 3. Im nächsten Schritt wird nur 3*2 + 0 = 6 gerechnet (statt 13*2 + 0 = 26). Dieses Ergebnis wird ebenso behandelt; der Zehner ist hier 0. Die letzte Rechnung (6*2 + 1), ergibt wieder 13. Der Einer dieses Ergebnisses ist die letzte Ziffer des Endergebnisses.
1 1 0 1 0 1 2 ) 2 6 12 6 12 1 3 6 3 6 3 0 0 1 0 1 Um die weiteren Ziffern zu berechnen, wird auf die in der letzten Zeile stehenden Zehner (00101) dasselbe Schema erneut angewandt. Dabei kann man die führenden Nullen vernachlässigen:
1 1 0 1 0 1 2 ) 2 6 12 6 12 1 3 6 3 6 3 0 0 1 0 1 2 ) 2 4 1 2 5 0 0 Da jetzt nur noch Nullen in der Übertragszeile stehen, ist das Verfahren beendet. Das Gesamtergebnis (53) liest man in der letzten Spalte der Einer von unten nach oben.
Vereinfachte Schreibweise
Das kaskadierte Horner-Schema kann durch etwas mehr Kopfrechnen stark vereinfacht dargestellt werden. Die Rechnung beschleunigt sich dadurch erheblich.
Die Ziffern der Ausgangszahl werden zunächst senkrecht untereinander geschrieben. Links daneben wird eine senkrechte Linie gezogen. Unterhalb der letzten Ziffer eine waagerechte Linie, unter der am Ende das Ergebnis steht.
Zuerst wird die höchstwertige Ziffer (die erste 1) eine Zeile tiefer in die vorhergehende Spalte übertragen. Diese steht jetzt links neben der zweiten Ziffer (ebenfalls eine 1). Die linke Zahl wird mit der Zahlenbasis (hier 2) multipliziert, die rechte Zahl addiert (1*2 + 1). Vom Ergebnis (3) wird der Zehner eine Spalte weiter links geschrieben, der Einer eine Zeile tiefer.
Das gleiche Verfahren wird mit dem Einer des Ergebnisses (3) und der nächsten Ziffer (0) durchgeführt. Das Ergebnis (3*2 + 0 = 6) wird ebenso notiert wie das vorige Ergebnis.
Die dritte Rechnung lautet 6*2 + 1 = 13, danach ist 3*2 + 0 = 6 und schließlich wieder 6*2 + 1 = 13 zu berechnen. Wie in den vorherigen Schritten werden Einer und Zehner des Ergebnisses diagonal untereinander geschrieben.
Unter der waagerechten Linie steht jetzt die letzte Ziffer des Endergebnisses (3).
1 1 0 1 0 1 (2) 1 1 1 0 1 0 1 (2) 1 0 1 1 3 0 1 0 1 (2) 1 0 1 1 0 3 0 6 1 0 1 (2) 1 0 1 1 0 3 0 1 6 1 3 0 1 (2) 1 0 1 1 0 3 0 1 6 1 0 3 0 6 1 (2) 1 0 1 1 0 3 0 1 6 1 0 3 0 1 6 1 3 (2) Zur Berechnung der weiteren Ziffern wird jetzt die führende Spalte mit den bisher unberücksichtigten Zehnern genauso behandelt wie die Ausgangszahl.
Die erste gültige Ziffer wird eine Zeile tiefer in die vorherige Spalte übertragen. Diese Zahl (1) wird mit der Basis (2) multipliziert und zum Produkt (2) die nächste Ziffer (0) addiert. Zehner und Einer des Ergebnisses (02) werden diagonal wie oben gezeigt in das Schema eingetragen.
Das Ergebnis der letzten Rechnung (2*2 + 1 = 05) wird ebenso eingetragen. Die Einer dieses Ergebnisses (5) sind die nächste Ziffer des Endergebnisses.
1 0 1 1 0 3 0 1 6 1 0 3 0 1 6 1 3 (2) 1 0 1 1 0 3 0 1 6 1 1 0 3 0 1 6 1 3 (2) 1 0 1 1 0 3 0 1 6 1 0 1 0 3 0 2 1 6 1 3 (2) 1 0 1 1 0 3 0 1 6 1 0 1 0 3 0 0 2 1 6 1 5 3 (2) 1 0 1 1 0 3 0 1 6 1 0 1 0 3 0 0 2 1 6 1 5 3 (2) Da in der Zehnerspalte nur noch Nullen stehen, ist die Rechnung beendet. Das Endergebnis (53) lässt sich jetzt in der Ergebniszeile ablesen, diesmal sogar in der richtigen Reihenfolge.
Verfahren für die umgekehrte Richtung
Auf die umgekehrte Weise lässt sich eine Dezimalzahl in eine Zahl eines anderen Zahlensystems umrechnen. An Stelle einer fortgesetzten Multiplikation mit der Basis des anderen Zahlensystems tritt eine fortgesetzte Division durch diese Zahl. Die Ziffern der Zahl im anderen Zahlensystem ergeben sich von rechts nach links durch die Divisionsreste.
In der Tabellenschreibweise werden die Ziffern der Ausgangszahl untereinander geschrieben und für das Ergebnis wird eine waagerechte Linie gezogen. Die senkrechte Linie wird hier jedoch rechts der Ziffern gezogen. Zur Erinnerung kann die Zahlenbasis rechts unten notiert werden.
5 3 (2) Die erste Ziffer, vermehrt um eine führende Null, (05) wird durch die Zahlenbasis (2) geteilt. Der Quotient (2) wird in die vorangehende Spalte geschrieben. Der Rest (1) in die Zeile darunter.
05 3 (2) 2 05 13 (2) Dieser Rest bildet mit der nächsten Ziffer (3) eine neue zweistellige Zahl (13). Diese Zahl wird wiederum durch die Basis geteilt, das Ergebnis (6 Rest 1) wie oben diagonal in das Schema eingetragen.
2 05 13 (2) 2 05 6 13 1 (2) Da jetzt alle Ziffern abgearbeitet sind, ist der Rest der letzten Rechnung (1) die letzte Ziffer des Endergebnisses.
Die nicht bearbeiteten Quotienten werden wie eine neue Dezimalzahl behandelt (26), auf die dasselbe Verfahren angewandt wird.
02 05 6 13 1 (2) 1 02 05 06 13 1 (2) 1 02 05 06 13 1 (2) 1 02 05 3 06 13 0 1 (2) Die gewonnene Ziffer ist eine 0. In der Spalte der unbearbeiteten Quotienten steht jetzt eine 13.
01 02 05 3 06 13 0 1 (2) 0 01 02 05 13 06 13 0 1 (2) 0 01 02 05 13 06 13 0 1 (2) 0 01 02 05 6 13 06 13 1 0 1 (2) Nach diesem Schritt steht in der Quotientenspalte eine 06. Die führende Null wird ignoriert, das Verfahren startet mit der 6.
0 01 02 05 06 13 06 13 1 0 1 (2) 0 01 02 05 3 06 13 06 13 0 1 0 1 (2) Die jetzt noch zu behandelnde Zahl ist 3.
0 01 02 05 03 06 13 06 13 0 1 0 1 (2) 0 01 02 05 1 03 06 13 06 13 1 0 1 0 1 (2) Jetzt ist nur noch eine 1 übrig.
0 01 02 05 01 03 06 13 06 13 1 0 1 0 1 (2) 0 01 02 05 0 01 03 06 13 06 13 1 1 0 1 0 1 (2) 0 01 02 05 0 01 03 06 13 06 13 1 1 0 1 0 1 (2) Nach der letzten Rechnung steht in der Quotientenspalte eine 0. Das Verfahren ist damit abgeschlossen. In der Ergebniszeile steht die gesuchte Zahl in richtiger Reihenfolge.
Polynomdivision
Polynomdivision mit linearem Divisor
Am folgendem Beispiel
wird zunächst die Polynomdivision mit einem linearem Divisor im Horner-Schema dargestellt.
Die Polynomdivision wird üblicherweise in einer schriftlichen Form durchgeführt.
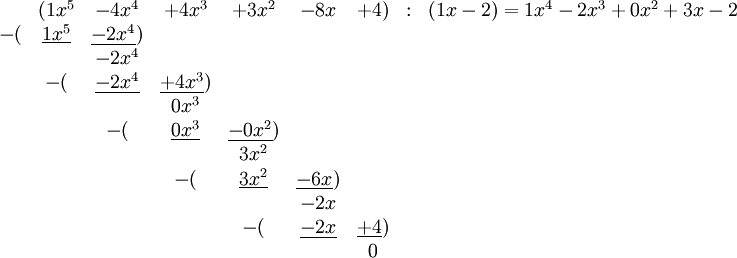
Lässt man nun die Potenzen von x weg, so erhält man folgende Darstellung:
( 1 −4 4 3 −8 4 ) : ( 1 −2 ) = 1 −2 0 3 −2 −( 1 −2 ) −2 −( −2 4 ) 0 −( 0 0 ) 3 −( 3 −6 ) −2 −( −2 4 ) 0 Verdichtet man nun dieses Schema auf drei Zeilen und übernimmt den ersten Koeffizienten des Dividenden in die dritte Zeile, so erhält man:
( 1 −4 4 3 −8 4 ) : ( 1 −2 ) −( −2 4 0 −6 4 ) 1 −2 0 3 −2 0 Wie man nun sieht, sind die doppelt unterstrichenen Werte der letzten Zeile die Koeffizienten des Ergebnispolynoms und der letzte Wert dahinter ist der Divisionsrest (hier Null).
Multipliziert man nun das Vorzeichen in die zweite Zeile, so erfolgt die Berechnung nach folgendem Ablauf:
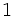
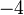
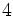
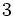
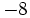
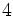
+ + + + + 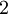
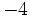
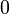
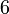
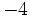
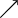
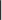
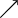
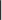
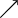
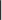
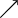
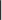
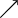
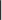
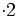
= 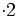
= 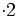
= 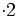
= 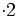
= 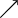
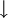
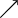
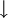
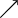
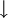
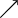
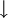
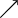
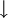
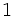
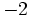
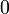
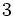
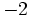
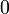
Vermerkt man nun noch den vorzeichengedrehten Wert des Absolutglieds des Divisors vor dem Schema, so bekommt man die allgemeine Darstellung des Horner-Schemas:
1 −4 4 3 −8 4 2) 2 −4 0 6 −4 1 −2 0 3 −2 0 Das obige Beispiel kann nun in folgender Formel zusammengefasst werden:
Hat die Divisionsaufgabe:
als Ergebnis
so bestimmen sich die Koeffizienten nach folgender Vorschrift:

Das Horner-Schema stellt sich dann wie folgt dar:
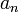
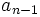
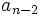
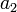
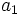
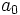
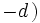
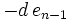
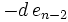

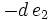
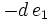
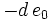
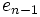
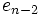
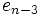
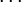
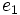
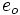

Anmerkung: Mit diesem Ergebnis lässt sich die Berechnung von Funktionswerten eines Polynoms P an der Stelle a auch folgendermaßen herleiten: Betrachten wir die Division P(x) durch x − a
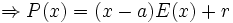
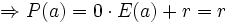
Polynomdivision mit einem Divisor 2. Grades
Hat die Divisionsaufgabe:
als Ergebnis
so bestimmen sich die Koeffizienten nach folgender Vorschrift:
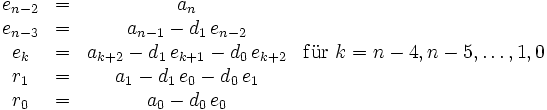
Das verallgemeinerte Horner-Schema stellt sich dann wie folgt da:
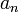
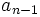
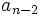
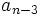
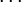
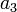
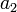
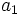
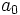
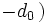
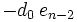
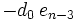

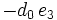
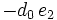
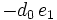
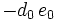
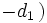
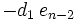
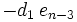
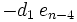

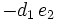
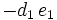
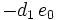
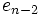
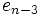
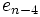
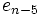
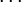
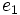
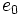
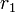
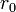
Ein Beispiel:
Im Horner-Schema:
−6 14 −8 −2 0 8 −6 −1 ) 6 −2 −2 0 2 2 ) −12 4 4 0 −4 −6 2 2 0 −2 4 −4 Daraus ergibt sich:
Lineartransformation
In einigen Fällen, beispielsweise zur Verbesserung der Konvergenz beim Newton-Verfahren, kann es sehr hilfreich sein, ein Polynom P in ein Polynom Pa, a konstant, zu transformieren, so dass mit x = a + y gilt:
Eine solche Lineartransformation kann man durch Einsetzen von a + y anstelle von x und anschließendes Ausmultiplizieren erhalten. Wesentlich effizienter lässt sich diese Rechnung mit dem vollständigen Horner-Schema durchführen.
Betrachten wir das Polynom
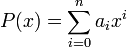 vom Grad n welches wir nach Potenzen von y = x − a entwickeln wollen: Hierzu dividieren wir das Polynom P(x) mittels des Horner-Schemas durch (x − a). Wie oben gezeigt können wir aus dem Schema das Polynom E1(x) und den Rest r0 ablesen, so dass gilt:
vom Grad n welches wir nach Potenzen von y = x − a entwickeln wollen: Hierzu dividieren wir das Polynom P(x) mittels des Horner-Schemas durch (x − a). Wie oben gezeigt können wir aus dem Schema das Polynom E1(x) und den Rest r0 ablesen, so dass gilt:Nun wird die Division auf das Ergebnis-Polynom E1(x) durchgeführt und erhalten E2 bzw. den Rest r1:
Nach n Divisionen erhält man:
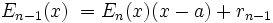 mit
mit 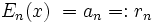
Es folgt:
Mit y = x − a ist dann die Lineartransformation Pa
D.h. die Reste bei der fortgesetzten Division mit dem Linearfaktor (x − a) bilden die Koeffizienten des transformierten Polynoms Pa
Beispiel
Möchte man z.B. die Nullstelle des Polynoms
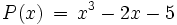 berechnen, so kann man leicht den Punkt x = 2 als erste Näherung raten. Für die weitere Berechnung ist es nun hilfreich P(x) nach x − 2 zu entwickeln (siehe „Methodus fluxionum et serierum infinitarum“). Gesucht ist also das Polynom P2(x) = P(x − 2).
berechnen, so kann man leicht den Punkt x = 2 als erste Näherung raten. Für die weitere Berechnung ist es nun hilfreich P(x) nach x − 2 zu entwickeln (siehe „Methodus fluxionum et serierum infinitarum“). Gesucht ist also das Polynom P2(x) = P(x − 2).1 0 −2 −5 2) 2 4 4 1 2 2 −1 2) 2 8 1 4 10 2) 2 1 6 Das gesuchte Polynom ist also
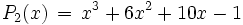 .
.Berechnung der Ableitung
Eine weitere Eigenschaft des Horner Schemas ist es, dass man recht schnell die erste Ableitung an der Stelle x0 berechnen kann.
Betrachten wir die Division
mit dem Ergebnis
welches wir aus dem Horner-Schema ablesen können. Weiter oben konnte man auch sehen, dass r = P(x0) ist. Es gilt also
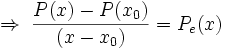
Die Ableitung
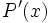 lässt sich mit dem Differenzenquotienten berechnen. Es gilt
lässt sich mit dem Differenzenquotienten berechnen. Es giltDaraus folgt
D.h. die Zahlen in der dritten Zeile des Horner-Schemas bilden die Koeffizienten für Pe(x0). Durch nochmalige Anwendung des Horner-Schemas kann dann schließlich der Wert der Ableitung
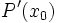 berechnet werden.
berechnet werden.Beispiel
Betrachten wir das Polynom P(x) = x5 − 4x4 + 4x3 + 3x2 − 8x + 4 an der Stelle x=2
1 −4 4 3 −8 4 2) 2 −4 0 6 −4 1 −2 0 3 −2 0 2) 2 0 0 6 1 0 0 3 4 Aus dem Schema kann man nun ablesen:
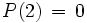 und
und 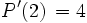
Probe
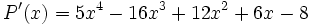
Aus dem Horner-Schema
5 −16 12 6 −8 2 ) 10 −12 0 12 5 −6 0 6 4 folgt
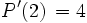 .
.Mehrfache Ableitungen
Auch die Werte der weiteren Ableitungen lassen sich aus dem Horner-Schema ablesen. Sei
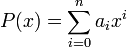 und
und 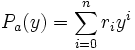 , mit x = a + y
, mit x = a + y
das Polynom welches wir aus dem vollständigen Horner-Schema ablesen können (siehe oben), so ist
Nullstellenbestimmung
Das Horner-Schema lässt sich in verschiedenen numerischen Verfahren zur Nullstellenbestimmung von Polynomen einsetzen.
Hat man z.B. eine Nullstelle „erraten“ so kann man, wie oben gezeigt wurde, schnell überprüfen ob die Vermutung stimmt.
Ein weiteres Einsatzgebiet ist das Newtonsche Näherungsverfahren. Für das Newton-Verfahren benötigt man in jedem Iterations-Schritt P(xn) und P'(xn). Diese Werte lassen sich, wie oben beschrieben, recht schnell mit dem Horner-Schema berechnen.
Geschichte
William George Horner war nicht der erste, der dieses Verfahren entdeckte. Er hatte es vor allem De Morgan zu verdanken, dass das Verfahren unter seinem Namen bekannt wurde. Paolo Ruffini veröffentlichte 15 Jahre vor Horner bereits ein entsprechendes Verfahren und es wird in Spanien daher auch als regla de Ruffini bezeichnet. Erste bekannte Beschreibungen des Verfahrens reichen bis in die Anfänge des 14. Jahrhunderts zurück. Der Chinese Zhu Shijie beschrieb bereits 1303 in seinem Buch Siyuan yujian eine Umwandlungsmethode zur Lösung von Gleichungen, die er fan fa nannte.
Quelle
- William George Horner. A new method of solving numerical equations of all orders, by continuous approximation. Philosophical Transactions of the Royal Society of London, Seiten 308-335, Juli 1819.
Einzelnachweise
- ↑ Josef Stoer: Numerische Mathematik 1. 9 Auflage. Springer, 2004.
Weblinks
Wikimedia Foundation.