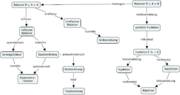
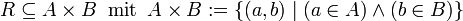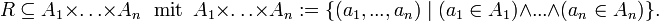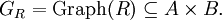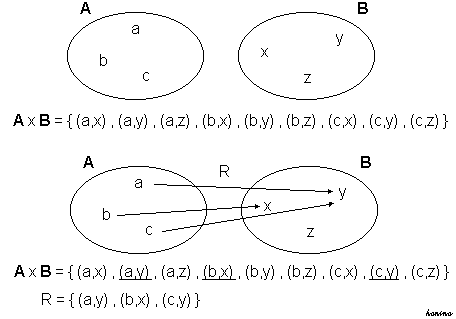- Relation (Mengentheorie)
-
Eine Relation ist allgemein eine Beziehung, die zwischen Dingen bestehen kann. Relationen im Sinne der Mathematik sind ausschließlich diejenigen Beziehungen, bei denen stets klar ist, ob sie bestehen oder nicht. Zwei Gegenstände können also nicht „bis zu einem gewissen Grade“ in einer Relation zueinander stehen.
Damit ist eine einfache mengentheoretische Definition des Begriffs der Relation möglich: Eine Relation R ist eine Menge von n-Tupeln. Dinge, die in der Relation R zueinander stehen, bilden ein n-Tupel, das Element von R ist.
Wenn nicht ausdrücklich etwas anderes angegeben ist, versteht man unter einer Relation eine "zweistellige" oder "binäre" Relation, also eine Beziehung zwischen je zwei Dingen. Die Elemente eines Paares (a,b) können aus verschiedenen Grundmengen A und B stammen; die Relation heißt dann heterogen oder "Relation zwischen den Mengen A und B". Wenn die Grundmengen übereinstimmen, A = B, heißt die Relation homogen oder "Relation in der Menge A". Wichtige Spezialfälle, zum Beispiel Äquivalenzrelationen und Ordnungsrelationen, sind Relationen in einer Menge.
Inhaltsverzeichnis
Definition
Die vorstehenden Überlegungen erlauben nun folgende formale Definition: Eine binäre Relation R ist eine Teilmenge des kartesischen Produkts zweier Mengen A und B:
Die Menge A wird als Vorbereich oder Quelle der Relation R bezeichnet; die Menge B als Nachbereich, Ziel oder Zielmenge[1]
Allgemeiner ist eine n-stellige Relation eine Teilmenge des kartesischen Produkts von n Mengen A1, ..., An.
Oft ist die obige Definition, insbesondere einer binären Relation, nicht präzise genug, und man muss die Quelle und Zielmenge in die Definition mit einbeziehen; obige Teilmenge ist dann genauer der Graph der Relation. Dann definiert man eine Relation als Tripel R = (GR,A,B) mit
Alternativ könnte man vereinbaren, dass ein Paar (a,b) hier die Mengen A und B als "Zielmengen" für den Index 1 bzw. 2 "beinhaltet".
Diese genauere Definition lässt sich offensichtlich direkt auf n-stellige Relationen verallgemeinern. Die Kenntnis von Quelle und Zielmenge ist jedoch besonders für binäre Relationen wichtig, u. a., wenn man Funktionen als spezielle (sogenannte funktionale) Relationen betrachtet.
Erläuterungen und Schreibweisen
Das kartesische Produkt ist die Menge aller geordneten Paare von a und b, wobei a irgendein Element aus der Menge A und b eines aus B darstellt. Bei dem geordneten Paar ist die Reihenfolge wichtig, d.h. (a,b) unterscheidet sich von (b,a), im Gegensatz zum ungeordneten Paar {a,b}, das identisch ist mit {b,a}.
Für
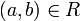 schreibt man meist „aRb“. Oft betrachtet man den Spezialfall B = A, also
schreibt man meist „aRb“. Oft betrachtet man den Spezialfall B = A, also 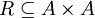 , die Relation heißt dann auch homogen. Manche Autoren definieren eine allgemeine Relation bereits als homogene Relation, denn eine allgemeine Relation
, die Relation heißt dann auch homogen. Manche Autoren definieren eine allgemeine Relation bereits als homogene Relation, denn eine allgemeine Relation 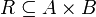 ist auch immer homogen:
ist auch immer homogen: 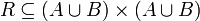 .
.Relationen und Funktionen
Einer Relation im obigen Sinn entspricht auf eindeutige Weise eine Funktion fR, deren Definitionsmenge das kartesische Produkt der Mengen ist und deren Zielmenge lediglich die Elemente wahr und falsch umfasst, wobei fR(a,b) zu aRb äquivalent ist. Diese Funktion ist auch als Indikatorfunktion oder charakteristische Funktion der Teilmenge
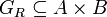 bekannt (wobei evtl. falsch = 0 und wahr = 1 genommen wird).
bekannt (wobei evtl. falsch = 0 und wahr = 1 genommen wird).Umgekehrt kann man aber auch eine Funktion als eine spezielle (nämlich als eine linkstotale und rechtseindeutige) Relation definieren (siehe unten). Ob man Funktionen als spezielle Relationen oder Relationen als spezielle Funktionen erklärt, bleibt willkürlich.
Verkettung von Relationen
Eine Relation
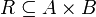 und eine Relation
und eine Relation 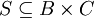 können miteinander verkettet werden. Das Ergebnis ist die Relation
können miteinander verkettet werden. Das Ergebnis ist die Relation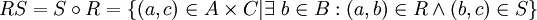 .
.
Dies ist eine Verallgemeinerung des bekannteren Konzepts der Verkettung von Funktionen.
Homogene Relationen
Ist
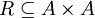 , dann nennt man die Relation homogen. In diesem Fall ist die Verkettung
, dann nennt man die Relation homogen. In diesem Fall ist die Verkettung 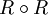 ebenfalls eine homogene Relation. Hier ist die Schreibweise
ebenfalls eine homogene Relation. Hier ist die Schreibweise 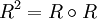 und allgemeiner
und allgemeiner 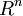 für
für 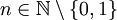 gebräuchlich. Das kann zu Verwechslungen mit dem kartesischen Produkt
gebräuchlich. Das kann zu Verwechslungen mit dem kartesischen Produkt 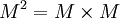 führen, das sich natürlich auch aus Relationen bilden lässt. Die Bedeutung ergibt sich aus dem Sinnzusammenhang.
führen, das sich natürlich auch aus Relationen bilden lässt. Die Bedeutung ergibt sich aus dem Sinnzusammenhang.Eine spezielle homogene Relation ist die Diagonale ΔA (oder auch nur Δ) auf einer Menge A. Dies ist nichts anderes als die Gleichheitsrelation als Teilmenge des kartesischen Produkts
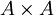 geschrieben:
geschrieben: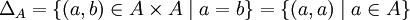 .
.
Diese Schreib- und Sprechweise kann verwendet werden, um gewisse Eigenschaften von Relationen in Mengenschreibweise kurz darzustellen.
Eine weitere spezielle homogene Relation ist die Allrelation oder universale Relation
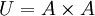 ,
,
die etwa in der Graphentheorie eine Rolle spielt. Ein Anwendungsbeispiel ist folgender Satz:
- Ist G = (V,E) ein gerichteter Graph mit Eckenmenge V und Kantenmenge
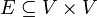 , so ist G genau dann (stark) zusammenhängend, wenn die reflexiv-transitive Hülle von E die Allrelation ist.
, so ist G genau dann (stark) zusammenhängend, wenn die reflexiv-transitive Hülle von E die Allrelation ist.
Umkehrrelation
Die Umkehrrelation (auch konverse Relation oder inverse Relation genannt) ist für eine Relation
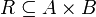 definiert als
definiert als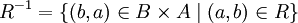 .
.
Beispiel
Alle möglichen Kombinationen von den Elementen aus der Menge A := {a,b,c} und B := {x,y,z}:
Eigenschaften (binär)
Die in den folgenden Tabellen gegebenen Beispiele beziehen sich bei Verwendung von Gleichheitszeichen "=", Kleinerzeichen "<" und Kleinergleich-Zeichen "≤" auf die gewöhnliche Anordnung reeller Zahlen.
Attribute für homogene Relationen
Die folgenden Attribute beschreiben gemeinsam eine Äquivalenzrelation, die Attribute reflexiv und transitiv sind auch für Ordnungsrelationen gebräuchlich:
Die Relation heißt wenn gilt (Aussagenlogik) oder gleichwertig (Mengenschreibweise) und das bedeutet reflexiv 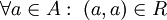
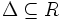
Jedes Element steht in Relation zu sich selbst, z. B. ist stets a≤a. symmetrisch 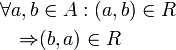
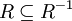
Die Relation ist ungerichtet, z. B. folgt aus a=b stets b=a transitiv 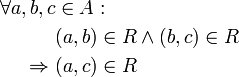
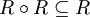
Anfang und Ende einer verbundenen Sequenz sind verbunden, z. B. folgt aus a<b und b<c stets a<c. Die folgenden Attribute werden zur Kennzeichnung von Ordnungsrelationen ebenfalls gebraucht:
Die Relation heißt wenn gilt (Aussagenlogik) oder gleichwertig (Mengenschreibweise) und das bedeutet irreflexiv (antireflexiv) 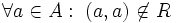
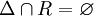
Kein Element steht in Relation zu sich selbst, z. B. gilt a<a für kein a. asymmetrisch 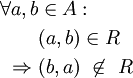
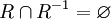
Es gibt keine zwei Elemente, die in beiden Richtungen in Relation stehen, z. B. folgt aus a<b stets, dass b<a nicht gilt. antisymmetrisch für beliebige bzw. identitiv für homogene Relationen 
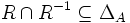
Es gibt keine zwei verschiedenen Elemente, die in beiden Richtungen in Relation stehen, z. B. folgt aus a≤b und b≤a stets a=b. total, linear oder konnex 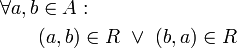
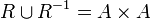
Je zwei Elemente stehen in Relation, z. B. gilt stets a≤b oder b≤a. trichotomisch 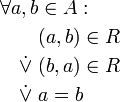
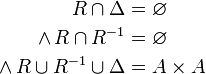
Je zwei Elemente sind entweder gleich, oder sie stehen in genau einer Art und Weise zueinander in Relation. alternativ 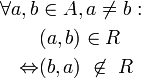
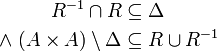
Es gilt für verschiedene Elemente stets genau eine der Relationen a R b oder b R a. Die folgenden Attribute sind besonders zur Beschreibung von Verknüpfungen gebräuchlich.
Die Relation heißt wenn gilt (Aussagenlogik) oder gleichwertig (Mengenschreibweise) und das bedeutet drittengleich oder rechtskomparativ 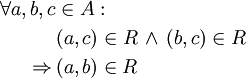
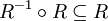
Stehen zwei Elemente jeweils zu einem dritten in Relation, dann stehen sie auch zueinander in Relation. Zu beachten ist, dass diese Forderung nicht äquivalent zur Transitivität ist. drittengleich oder linkskomparativ 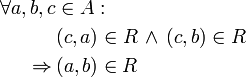
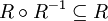
Die folgenden Attribute werden seltener gebraucht:
Die Relation heißt wenn gilt (Aussagenlogik) oder gleichwertig (Mengenschreibweise) und das bedeutet intransitiv 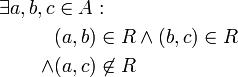
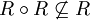
Nicht bei jeder verbundenen Sequenz sind Anfang und Ende verbunden. antitransitiv 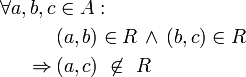
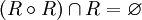
Bei keiner verbundenen Sequenz sind Anfang und Ende verbunden. Attribute für Relationen zwischen verschiedenen Mengen
Die folgenden Relationen sind für Funktionen (dargestellt als spezielle Relationen) wichtig. Im Allgemeinen besteht hier die Relation R zwischen zwei verschiedenen Mengen
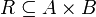 , der Fall A = B ist natürlich auch möglich. Die Abbildungen p1 und p2 bezeichnen die Projektionen auf die erste bzw. zweite Faktormenge des kartesischen Produkts
, der Fall A = B ist natürlich auch möglich. Die Abbildungen p1 und p2 bezeichnen die Projektionen auf die erste bzw. zweite Faktormenge des kartesischen Produkts 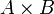 .
.Die Relation heißt wenn gilt (Aussagenlogik) oder gleichwertig (Mengenschreibweise) und das bedeutet linkstotal 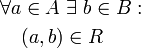
p1(R) = A Jedes Element aus A steht zu mindestens einem Element von B in Relation. surjektiv bzw. rechtstotal 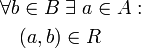
p2(R) = B Jedes Element aus B hat mindestens einen Partner in A. injektiv bzw. linkseindeutig 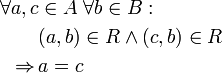
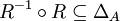
Kein Element aus B hat mehr als einen Partner in A. funktional bzw. rechtseindeutig 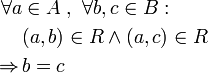
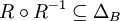
Kein Element aus A hat mehr als einen Partner in B bijektiv bzw. eineindeutig oder umkehrbar eindeutig 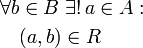
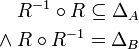
Jedes Element aus B hat genau einen Partner in A Eine Relation R heißt Funktion, wenn sie linkstotal und rechtseindeutig ist. Eine linkstotale Relation wird auch Korrespondenz genannt. Die Attribute injektiv, surjektiv und bijektiv werden in der Regel für Funktionen gebraucht.
Relationszeichen
In der elementaren Mathematik gibt es drei grundlegende Vergleichsrelationen:
- x < y (Beispiel: 2 < 3 "2 ist kleiner als 3")
- x = y (Beispiel: 3 = 3 "3 ist gleich 3")
- x > y (Beispiel: 3 > 2 "3 ist größer als 2")
mit
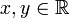 .
.Zwei reelle Zahlen stehen immer in genau einer dieser Relationen zueinander. Mit diesen Relationszeichen lassen sich auch weitere erschaffen; so gilt:
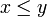 , falls x < y oder x = y (Beispiel:
, falls x < y oder x = y (Beispiel: 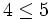 )
)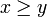 , falls x > y oder x = y (Beispiel:
, falls x > y oder x = y (Beispiel: 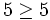 )
)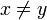 , falls x < y oder x > y (Beispiel:
, falls x < y oder x > y (Beispiel: 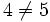 )
)
für alle
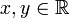 .
.Für komplexe Zahlen existieren obige Ordnungsrelationen nicht.
Mathematiker verwenden das Zeichen ≤ auch für abstrakte Ordnungsrelationen (und ≥ für die zugehörige Umkehrrelation) während "<" keine Ordnungsrelation im Sinne der mathematischen Definition ist.
Für Äquivalenzrelationen werden "symmetrische" Symbole wie ≈ , ~ , ≡ bevorzugt.
Klassen von Relationen
Wichtige Klassen von Relationen:
- Eine Äquivalenzrelation ist reflexiv, transitiv und symmetrisch.
- Eine Funktion ist linkstotal und rechtseindeutig (d.h. N:1).
- Eine Verträglichkeitsrelation oder Toleranzrelation ist reflexiv und symmetrisch (nicht notwendig transitiv).
- Eine Quasiordnung oder Präordnung ist reflexiv und transitiv (nicht notwendig symmetrisch oder antisymmetrisch).
- Eine Halbordnung oder partielle Ordnung ist reflexiv, transitiv und antisymmetrisch. (Halbordnung = Präordnung + antisymmetrisch)
- Eine lineare Ordnung oder totale Ordnung ist reflexiv, transitiv, antisymmetrisch und total (linear). (Lineare Ordnung = Halbordnung + total)
- Eine strenge Halbordnung oder Striktordnung ist transitiv und irreflexiv.
- Eine lineare Striktordnung oder strenge Totalordnung ist eine trichotomische Striktordnung.
Achtung: eine lineare Striktordnung ist nicht linear, eine strenge Totalordnung nicht total! - Eine Wohlordnung ist eine lineare Ordnung, bei der jede nichtleere Teilmenge von A ein kleinstes Element besitzt.
Alternative Sprechweisen
- Zu linkseindeutig sagt man auch injektiv oder voreindeutig.
- Zu linkstotal sagt man auch vordefiniert.
- Zu rechtseindeutig sagt man auch nacheindeutig.
- Zu rechtstotal sagt man auch surjektiv oder nachdefiniert.
- Zu eineindeutig sagt man auch bijektiv.
Siehe auch
Operationen auf ganzen Relationen werden in der relationalen Algebra behandelt.
In der Informatik sind Relationen für relationale Datenbanken wichtig.Einzelnachweise
- ↑ Walter Gellert, Herbert Kästner, Siegfried Neuber (Hrsg): Lexikon der Mathematik, VEB Bibliographisches Institut Leipzig, 1979. S 484, Relation.
Wikimedia Foundation.