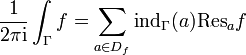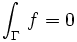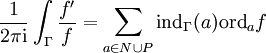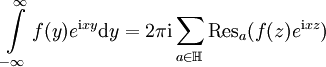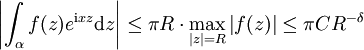- Residuum (Mathematik)
-
Der Residuensatz ist ein wichtiger Satz der Funktionentheorie, eines Teilgebietes der Mathematik. Er stellt eine Verallgemeinerung des Cauchyschen Integralsatzes und der Cauchyschen Integralformel dar. Seine Bedeutung liegt nicht nur in den weitreichenden Folgen innerhalb der Funktionentheorie, sondern auch in der praktischen Berechnung von reellen Integralen.
Inhaltsverzeichnis
Residuensatz
Der Residuensatz besagt, dass das Kurvenintegral längs einer geschlossenen Kurve über eine bis auf isolierte Singularitäten holomorphe Funktion lediglich vom Residuum in den Singularitäten, im Innern der Kurve und der Windungszahl der Kurve um diese Singularitäten abhängt. Anstelle eines Kurvenintegrals muss man also nur Residuen und Windungszahlen berechnen, was in vielen Fällen einfacher ist.
Satz
Ist
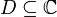 ein Gebiet, Df diskret in D und
ein Gebiet, Df diskret in D und 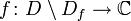 holomorph, gilt für jeden nullhomologen Zyklus Γ in D mit
holomorph, gilt für jeden nullhomologen Zyklus Γ in D mit 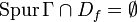 und der zugehörigen Windungszahl
und der zugehörigen Windungszahl 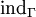 :
:Die Summe auf der rechten Seite ist stets endlich, denn Γ ist nullhomolog, und damit liegt
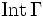 relativ kompakt in D und ist insbesondere beschränkt. Weil Df diskret in D ist, ist
relativ kompakt in D und ist insbesondere beschränkt. Weil Df diskret in D ist, ist 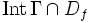 endlich, und nur dies sind die Punkte, die zu der Summe beitragen, denn für alle anderen verschwindet die Windungszahl oder das Residuum.
endlich, und nur dies sind die Punkte, die zu der Summe beitragen, denn für alle anderen verschwindet die Windungszahl oder das Residuum.Bemerkungen
- Handelt es sich bei den Punkten in Df um hebbare Singularitäten, verschwindet das Residuum in diesen Punkten, und man erhält den Integralsatz von Cauchy:
- Ist f auf D holomorph und
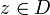 , hat
, hat 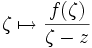 einen Pol 1. Ordnung in z mit Residuum f(z), und man erhält die Integralformel von Cauchy:
einen Pol 1. Ordnung in z mit Residuum f(z), und man erhält die Integralformel von Cauchy: 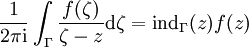
Null- und Polstellen zählendes Integral
Ist
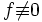 auf D meromorph mit der Nullstellenmenge N, der Polstellenmenge P und
auf D meromorph mit der Nullstellenmenge N, der Polstellenmenge P und 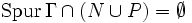 , dann folgt mit dem Residuensatz:
, dann folgt mit dem Residuensatz:Dabei bezeichnet
die Null- bzw. Polstellenordnung von f in a. Mit der Rechenregel des Residuums für die logarithmische Ableitung gilt
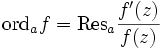 .
.Praktische Anwendung
Mit dem Residuensatz kann man reelle Integrale mit unendlichen Integrationsgrenzen berechnen. Dazu führt man in der komplexen Ebene eine geschlossene Kurve ein, die die reellen Integrationsgrenzen überdeckt; das Integral über den übrigen Teil der Kurve ist meist so konstruiert, dass es nach dem Grenzübergang verschwindet. Die komplexe Ebene wird dabei durch einen Punkt im Unendlichen ergänzt (Riemannsche Zahlenkugel). Dieses Berechnungsverfahren für uneigentliche reelle Integrale wird in der theoretischen Physik oft als "Methode der Residuen" bezeichnet.
Gebrochenrationale Funktionen
Ist
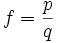 Quotient zweier Polynome mit
Quotient zweier Polynome mit 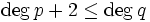 und
und 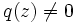 für alle
für alle 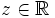 , ist
, ist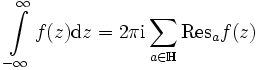 ,
,
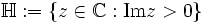 die obere Halbebene, denn man kann mit
die obere Halbebene, denn man kann mit ![\alpha\colon [0,\pi]\to\mathbb{C}](/pictures/dewiki/49/1cdb727e12c70c797251744bf5465273.png) ,
, 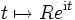 für ein großes
für ein großes 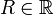 , über den geschlossenen Halbkreis
, über den geschlossenen Halbkreis ![\Gamma := [-R,R] \oplus \alpha](/pictures/dewiki/100/dddbe8f255a6c2677079af361506d3e5.png) integrieren und den Grenzübergang
integrieren und den Grenzübergang 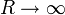 vollziehen. Wegen
vollziehen. Wegen 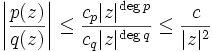 für großes | z | und Konstanten
für großes | z | und Konstanten 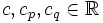 folgt mit der Standardabschätzung für Kurvenintegrale
folgt mit der Standardabschätzung für Kurvenintegrale 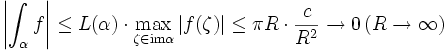 , also gilt
, also gilt 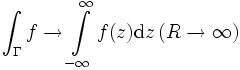 und wegen der obigen Abschätzung existiert letzteres Integral auch. Mit dem Residuensatz folgt die Berechnungsformel.
und wegen der obigen Abschätzung existiert letzteres Integral auch. Mit dem Residuensatz folgt die Berechnungsformel.Sei beispielsweise
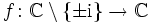 ,
, 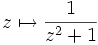 mit Polen 1. Ordnung in
mit Polen 1. Ordnung in 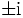 . Dann ist
. Dann ist 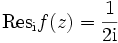 , und damit
, und damit 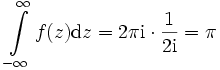 .
.Trigonometrische Funktionen
Ist
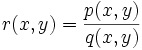 Quotient zweier Polynome mit
Quotient zweier Polynome mit 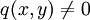 für alle
für alle 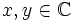 mit x2 + y2 = 1, ist
mit x2 + y2 = 1, ist-
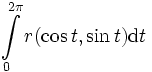
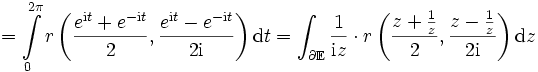
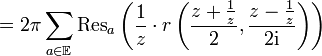 ,
,
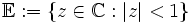 die Einheitskreisscheibe, denn die Windungszahl der Einheitskreislinie ist im Innern des Einheitskreises 1, und nach Voraussetzung liegen keine Singularitäten auf der Einheitskreislinie.
die Einheitskreisscheibe, denn die Windungszahl der Einheitskreislinie ist im Innern des Einheitskreises 1, und nach Voraussetzung liegen keine Singularitäten auf der Einheitskreislinie.Beispiel:
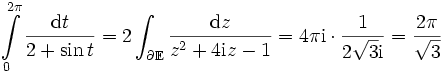 , denn
, denn 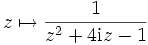 hat in
hat in 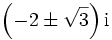 Pole 1. Ordnung, aber nur der Pol bei
Pole 1. Ordnung, aber nur der Pol bei 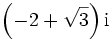 liegt in
liegt in 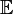 , und dort hat f(z) das Residuum
, und dort hat f(z) das Residuum 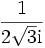 .
.Fouriertransformierte
Gegeben sei eine Funktion
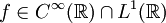 . Ferner gebe es Punkte
. Ferner gebe es Punkte 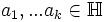 mit
mit 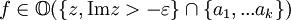 , wobei
, wobei  sei. Gibt es dann zwei Zahlen C,δ > 0 mit
sei. Gibt es dann zwei Zahlen C,δ > 0 mit 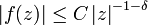 für große
für große 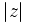 , so gilt für alle x > 0 die Formel
, so gilt für alle x > 0 die FormelDer Beweis erfolgt wie oben durch Integration über den oberen Halbkreis der komplexen Ebene, wobei das Integral über den Bogen α wegen
im Grenzfall
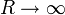 verschwindet.
verschwindet.Globale Fassung
Im globalen Kontext einer kompakten riemannschen Fläche lautet der Residuensatz:
- Die Summe der Residuen einer meromorphen 1-Form ist gleich null.
Als Folgerung ergibt sich damit sofort der zweite Satz von Liouville über elliptische Funktionen.
Literatur
- Kurt Endl, Wolfgang Luh: Analysis III. Aula-Verlag 1987 (6-te Auflag), ISBN 3-89104-456-9, S. 229
- Wolfgang Fischer, Ingo Lieb: Funktionentheorie. Vieweg 1994 (7-te Auflage), ISBN 3-528-67247-1, S. 145 Satz 4.1
Weblinks
- Residuensatz bei der FAQ von de.sci.physik
- Residuensatz in einem Skriptum der Uni Wuppertal
- Eric W. Weisstein: Residuensatz (engl.) auf MathWorld (englisch)
- Residuensatz bei PlanetMath (engl.)
- Residuum und Residuensatz in der Encyclopaedia of Mathematics (engl.)
Wikimedia Foundation.