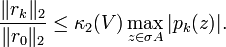- GMRES
-
Das GMRES-Verfahren (für Generalized minimal residual method) ist ein iteratives numerisches Verfahren zur Lösung großer, dünnbesetzter linearer Gleichungssysteme. Das Verfahren ist aus der Klasse der Krylow-Unterraum-Verfahren und insbesondere auch für nicht-symmetrische Matrizen geeignet. In exakter Arithmetik, also wenn ohne Rundungsfehler gerechnet wird, liefert das Verfahren nach endlich vielen Schritten die exakte Lösung. Interessanter ist es jedoch als näherungsweises Verfahren, da es mit einer geeigneten Vorkonditionierung auch Gleichungssysteme mit Millionen Unbekannten in wenigen Iterationen mit befriedigender Genauigkeit lösen kann. Damit stellt es eine Art Black Box-Löser für dünnbesetzte lineare Gleichungssysteme dar. Es wurde 1986 von Yousef Saad und Martin H. Schultz entwickelt.
Inhaltsverzeichnis
Das Verfahren
Gegeben sei das lineare Gleichungssystem Ax = b mit einer reellen
 Matrix A. Das Gleichungssystem sei eindeutig lösbar, A habe also vollen Rang. Gegeben sei außerdem eine Startnäherung x0, etwa einfach die rechte Seite b. Dann wird das GMRES-Verfahren dadurch definiert, dass im m-ten Schritt die euklidische Norm des Residuums
Matrix A. Das Gleichungssystem sei eindeutig lösbar, A habe also vollen Rang. Gegeben sei außerdem eine Startnäherung x0, etwa einfach die rechte Seite b. Dann wird das GMRES-Verfahren dadurch definiert, dass im m-ten Schritt die euklidische Norm des Residuums 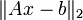 über den affinen Krylow-Unterraum
über den affinen Krylow-Unterraum 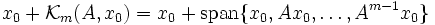 minimiert wird.
minimiert wird.Hierzu wird eine orthonormale Basis {v1,...,vm} des Raumes mit Hilfe der Arnoldi-Prozedur iterativ berechnet. Diese erlaubt eine Darstellung der von den Basisvektoren gebildeten Matrizen
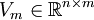 und
und 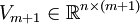 über eine Matrix
über eine Matrix 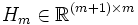 , die eine obere Hessenbergmatrix ist, an die eine Zeile angehängt wurde, in der nur der letzte Eintrag nicht Null ist, als
, die eine obere Hessenbergmatrix ist, an die eine Zeile angehängt wurde, in der nur der letzte Eintrag nicht Null ist, als- AVm = Vm + 1Hm.
Damit ist eine effizient berechenbare Form des Residuums gegeben, da Vm + 1 die 2-Norm erhält:
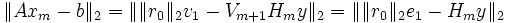 .
.
Hierbei bezeichnet
 den ersten Einheitsvektor. Die Hessenbergmatrix H wird in jedem Schritt aufdatiert und dann durch eine zusammengesetzte orthogonale Transformation Qm, meist durch Givens-Rotationen wie im unten abgegebenen Pseudo-Code, auf eine rechte obere Dreiecksmatrix
den ersten Einheitsvektor. Die Hessenbergmatrix H wird in jedem Schritt aufdatiert und dann durch eine zusammengesetzte orthogonale Transformation Qm, meist durch Givens-Rotationen wie im unten abgegebenen Pseudo-Code, auf eine rechte obere Dreiecksmatrix 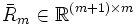 mit Nullen in der letzten Zeile, gebracht. Hier sind nur m-1 Rotationen notwendig, da jede ein Element auf der unteren Nebendiagonalen auf Null setzen kann. In manchen Fällen verlieren die berechneten Vektoren aufgrund von Rundungsfehlern ihre Orthogonalität. Dies kann meist durch Verwendung der aufwändigeren Householder-Spiegelungen statt der Drehungen behoben werden. Anwendung von Qm liefert in beiden Fällen
mit Nullen in der letzten Zeile, gebracht. Hier sind nur m-1 Rotationen notwendig, da jede ein Element auf der unteren Nebendiagonalen auf Null setzen kann. In manchen Fällen verlieren die berechneten Vektoren aufgrund von Rundungsfehlern ihre Orthogonalität. Dies kann meist durch Verwendung der aufwändigeren Householder-Spiegelungen statt der Drehungen behoben werden. Anwendung von Qm liefert in beiden Fällen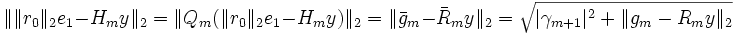 ,
,
wobei gm und Rm aus ihren Pendants durch weglassen der letzten Zeile erhalten werden. Hier ist nun ersichtlich, an welcher Stelle das Residuum minimal wird, nämlich für den eindeutig bestimmten Vektor y, der gm = Rmy erfüllt. Das Residuum im m-ten Schritt ist damit genau | γm + 1 | .
Eine Besonderheit des Verfahrens ist, dass die aktuelle Näherung xm im Laufe der Iteration zunächst nicht berechnet wird, sondern nur der Hilfsvektor y. Stattdessen liefert das Verfahren in jedem Schritt die Norm des Residuums. Ist diese kleiner als die gewünschte Genauigkeit wird das Verfahren üblicherweise abgebrochen. Dann wird die aktuelle Näherung als Linearkombination der Basisvektoren berechnet. Hierbei sind die Komponenten von y einfach die Koeffizienten der Basisdarstellung.
Alternativ ist die Lösung des obigen Minimierungsproblems gegeben als der Vektor xm des affinen Krylow-Unterraumes
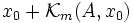 , dessen Residuum b − Axm senkrecht auf dem Raum
, dessen Residuum b − Axm senkrecht auf dem Raum  steht. Damit ist GMRES eine schiefe Projektionsmethode.
steht. Damit ist GMRES eine schiefe Projektionsmethode.Pseudocode
Gegeben
 , berechne r0 = b − Ax0.
, berechne r0 = b − Ax0.If r0 = 0, then END.
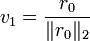 .
.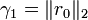 .
.For j = 1,...,n
- For i = 1,...,j do
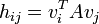 .
.
- For i = 1,...,j − 1 do
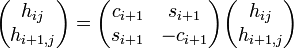 .
.
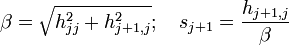 .
.
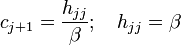 .
.
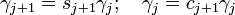 .
.
- if
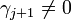 ,
, 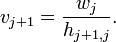
- else
-
- for i = j,...,1 do
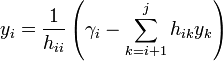 .
.
- for i = j,...,1 do
-
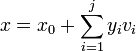 .
.
-
- END.
Konvergenzresultate
Aufgrund der Definition des Verfahrens über das Minimierungsproblem fällt die euklidische Norm der Residuen monoton. In exakter Arithmetik ist GMRES sogar ein direktes Lösungsverfahren, welches spätestens nach n Schritten die exakte Lösung liefert. Wird die Dimension des Krylow-Unterraums in jedem Schritt um eins erhöht, ist diese Aussage klar, da dann im letzten Schritt über den kompletten
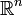 minimiert wird. Ist dies nicht der Fall, so kommt es vorher zu einem Abbruch des Algorithmus, allerdings mit der exakten Lösung.
minimiert wird. Ist dies nicht der Fall, so kommt es vorher zu einem Abbruch des Algorithmus, allerdings mit der exakten Lösung.Für allgemeine Matrizen ist dies auch das stärkste Ergebnis das möglich ist, denn nach einem Satz von Greenbaum, Pták und Strakoš gibt es zu jeder monoton fallenden Folge eine Matrix, so dass die Folge der durch GMRES erzeugten Residuen der gegebenen Folge entspricht. Insbesondere ist es also möglich, dass die Residuen konstant bleiben und erst im allerletzten Schritt auf Null fallen.
Für spezielle Matrizen gibt es schärfere Konvergenzresultate. Ist die Matrix diagonalisierbar, so existiert eine reguläre Matrix V und eine Diagonalmatrix Λ mit A = VΛV − 1. Dann gilt für jedes Polynom vom Grad k mit p(0) = 1:
Hierbei bezeichnet κ2 die Konditionszahl der Matrix in euklidischer Norm und σ(A) das Spektrum, also die Menge der Eigenwerte. Für eine normale Matrix ist κ2(V) = 1. Aus der Ungleichung folgt insbesondere, dass die Vorkonditionierung die Eigenwerte zu Clustern zusammenführen sollte.
Ist die Matrix positiv definit, das heißt alle ihre Eigenwerte sind größer als Null, so gilt:
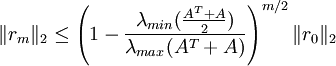 ,
,
wobei λmin und λmax den größten beziehungsweise kleinsten Eigenwert einer Matrix bezeichnen.
Ist die Matrix A nicht nur positiv definit, sondern auch symmetrisch, so gilt sogar:
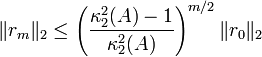 .
.
All diese Aussagen gelten nur für die Residuen und geben damit keine Auskunft über den tatsächlichen Fehler, also den Abstand der aktuellen Näherung zur exakten Lösung. Zu diesem sind keine Aussagen bekannt.
Aufwand und Restarted GMRES
GMRES benötigt pro Iteration eine Matrix-Vektor-Multiplikation und eine Reihe von Skalarprodukten, deren Anzahl um eine pro Iterationsschritt steigt, ebenso wie die Anzahl der (vollbesetzten!) zu speichernden Basisvektoren. Dies liegt daran, dass das Verfahren nicht durch eine kurze Rekursion gegeben ist, sondern auf alle Basisvektoren in jedem Schritt zugegriffen wird.
Da der Aufwand und der Speicherplatz linear mit der Iterationszahl steigen, ist es üblich, nach k Schritten die berechnete Basis zu verwerfen und die Iteration mit der aktuellen Näherungslösung neu zu starten (=Restart). Dieses Verfahren wird GMRES(k) genannt, übliche Restart-Längen sind 20 bis 40. Hier lässt sich allerdings nur noch für Spezialfälle Konvergenz beweisen, und es lassen sich Matrizen angeben, so dass ein Restart nicht zu Konvergenz führt.
Der Gesamtaufwand von GMRES ist wie bei allen Krylow-Unterraum-Verfahren bei dünnbesetzten Matrizen O(n) mit einer hohen Konstanten, wenn deutlich weniger Iterationen durchgeführt werden, als es Unbekannte gibt.
Vergleich mit anderen Lösern
Für symmetrische Matrizen fällt das Arnoldi-Verfahren zur Berechnung der orthogonalen Basis mit dem Lanczos-Verfahren zusammen. Das entsprechende Krylow-Unterraum-Verfahren ist das MinRes-Verfahren (für Minimal Residual Method) von Paige und Saunders. Dieses kommt im Gegensatz zur verallgemeinerten Variante mit einer Dreitermrekursion aus. Es lässt sich zeigen, dass es für allgemeine Matrizen kein Krylow-Unterraum-Verfahren gibt, welches mit kurzen Rekursionen arbeitet, aber gleichzeitig wie das GMRES-Verfahren eine Optimalitätsbedingung bezüglich der Norm des Residuums, erfüllt.
Eine andere Klasse von Verfahren baut auf dem unsymmetrischen Lanczos-Verfahren auf, insbesondere das BiCG-Verfahren. Solche Verfahren zeichnen sich durch eine Dreitermrekursion aus, allerdings haben sie aufgrund der fehlenden Optimalität keine monotone Konvergenzhistorie mehr. Darüber hinaus liefern sie zwar im Konvergenzfall die exakte Lösung, haben allerdings keine garantierte Konvergenz mehr.
Die dritte Variante sind Verfahren wie CGS und BiCGSTAB. Diese arbeiten ebenfalls mit Dreitermrekursionen ohne Optimalität und können ebenfalls vorzeitig ohne Konvergenz abbrechen. Die Idee bei diesen Verfahren ist es, die generierenden Polynome der Iterationssequenz geschickt zu wählen.
Keine der drei Gruppen ist für alle Matrizen besser, es gibt jeweils Beispiele wo eine Klasse die anderen übertrumpft. In der Praxis werden deswegen mehrere Löser ausprobiert, um für das gegebene Problem Erfahrungswerte zu sammeln.
Vorkonditionierung
Weniger entscheidend als die Auswahl des tatsächlichen Lösers ist die Wahl des Vorkonditionierers, durch den entscheidende Geschwindigkeitsverbesserungen erzielt werden können. Für sequentielle Codes bietet sich hier eine ILU-Zerlegung an, aber je nach Problem können sich auch andere Vorkonditionierer als sehr effizient erweisen. Da ILU nicht parallelisierbar ist, werden in diesem Falle andere eingesetzt, beispielsweise Schwarz-Gebietszerlegungs-Verfahren.
Literatur
- C. T. Kelley: Iterative Methods for Linear and Nonlinear Equations, SIAM, ISBN 0-89871-352-8
- Andreas Meister: Numerik linearer Gleichungssysteme, 2. Auflage, Vieweg, Wiesbaden 2005, ISBN 3-528-13135-7
- Yousef Saad: Iterative Methods for Sparse Linear Systems, 2nd edition, SIAM Society for Industrial & Applied Mathematics 2003, ISBN 0-898-71534-2
- Yousef Saad, Martin H. Schultz: GMRES: A generalized minimal residual algorithm for solving nonsymmetric linear systems, SIAM Journal on Scientific and Statistical Computing, Band 7, S. 856-869. Society for Industrial and Applied Mathematics, Philadelphia 1986, ISSN 0196-5204
Wikimedia Foundation.