Satz der Identität

In logischen Systemen wird Identität über Ununterscheidbarkeit eingeführt: Das Identitätsprinzip besagt, dass ein Gegenstand A genau dann mit einem Gegenstand B identisch ist, wenn sich zwischen A und B kein Unterschied finden lässt. Die Methode, durch die Identität erkannt wird, ist der Vergleich. Das Identitätsprinzip wird oft Gottfried Wilhelm Leibniz zugeschrieben und daher auch Leibniz-Gesetz (Leibniz' law) genannt.

Intuitive Rechtfertigung

Das Identitätsprinzip lässt sich in zwei Forderungen aufspalten:

• die Identität ununterscheidbarer Dinge
• die Ununterscheidbarkeit identischer Dinge

Die Identität Ununterscheidbarer

Die Identität Ununterscheidbarer besagt, dass, wenn Dinge ununterscheidbar sind, sie auch identisch sind, bzw. äquivalent: Sind sie nicht identisch, so muss es einen Unterschied zwischen ihnen geben. Zum Beispiel müssen sich zwei verschiedene Münzen, auch wenn sie absolut gleich aussehen, in irgendeiner Hinsicht unterscheiden, etwa durch ihre Lage im Raum.

Die Ununterscheidbarkeit Identischer

Die Ununterscheidbarkeit Identischer besagt, dass identische Dinge ununterscheidbar bzw. äquivalent sind: Gibt es einen Unterschied zwischen ihnen, so können sie nicht identisch sein. Stellt man fest, dass eine Münze ganz aus Kupfer und eine ganz aus Gold ist, kann es sich nicht um dieselbe Münze handeln, weil diese dann sowohl aus Kupfer als auch aus Gold wäre, was offensichtlich widersprüchlich ist.

Geschichtliche Betrachtung

Die philosophische Formulierung eines Prinzips der „Identität des Ununterscheidbaren“ geht weit zurück, und findet sich schon in Überlegungen der Stoiker, die moderne Sichtweise zur Identität geht auf Betrachtungen von Leibniz zurück. Die historische Diskussion der intuitiven Eigenschaften von Ununterscheidbarem findet sich meist unter seinem lateinischen Schlagwort als principium identitatis indiscernibilium.

Diskussion

Verschiedene Formulierungen des Identitätsprinzips

Vom Identitätsprinzip gibt es verschiedene Formulierungen. Die erste ist die allgemeinverständlichste, aber unpräziseste, die letzte die komplizierteste, aber präziseste:

1. Ein Gegenstand A ist genau dann mit einem Gegenstand B identisch, wenn es zwischen A und B keinen Unterschied gibt.
2. Ein Gegenstand A ist genau dann mit einem Gegenstand B identisch, wenn alle Eigenschaften, die A zukommen, auch B zukommen und umgekehrt.
3. Seien „A“ und „B“ Ausdrücke für Gegenstände. Dann gilt: „A“ und „B“ bezeichnen genau dann denselben Gegenstand, wenn sich „A“ für „B“ in allen Aussagen bei Erhaltung des Wahrheitswertes ersetzen lässt.

Erläuterung

Der Zusammenhang zwischen den ersten beiden Formulierungen ergibt sich dadurch, dass ein Unterschied zwischen zwei Dingen immer mit einer Eigenschaft einhergeht, die einem Ding zukommt und dem anderen nicht. So könnte beispielsweise ein Farb-Unterschied darin bestehen, dass dem einen Ding die Eigenschaft „Rot“ zukommt, dem anderen nicht.

Nummer drei ist eine Fassung von Leibniz berühmter Formulierung „Eadem sunt quae sibi ubique substitui possunt, salva veritate“ („Dieselben sind, die sich überall ersetzen können, bei Wahrung von Wahrheit“). Bei der Erläuterung gehen wir zunächst von zwei Ausdrücken für denselben Gegenstand aus, z. B. von

• der höchste Berg der Erde
• der Mount Everest

Ersetzen wir nun in der Aussage:

Der Mount Everest liegt im Himalaya

„Mount Everest“ durch „der höchste Berg der Erde“ erhalten wir:

Der höchste Berg der Erde liegt im Himalaya

Das Identitätsprinzip besagt nun, dass diese Substitution den Wahrheitswert erhält, d. h. wenn der erste Satz wahr ist, muss dies auch der zweite Satz sein und umgekehrt. Tatsächlich muss dies für alle Sätze gelten, in denen der eine Ausdruck vorkommt. Wenn wir dagegen von Ausdrücken ausgehen, die nicht denselben Gegenstand bezeichnen, wie

• das Matterhorn
• der Mount Everest

so muss es laut Identitätsprinzip einen Satz geben, in dem eine entsprechende Ersetzung den Wahrheitswert nicht erhält. Ein solcher Satz ist beispielsweise:

Das Matterhorn ist über 8 000 Meter hoch.

Dieser Satz ist falsch, ersetzen wir aber in ihm „Matterhorn“ durch „Mount Everest“, so erhalten wir den wahren Satz:

Der Mount Everest ist über 8 000 Meter hoch.

Das Identitätsprinzip gilt uneingeschränkt nur in so genannten „extensionalen“ Sprachen wie z. B. der Sprache der Mathematik. In „intensionalen“ Sprachen (wie der deutschen Umgangssprache) gilt es nur mit Einschränkungen. Dieses Problem betrifft nur das Prinzip der Ununterscheidbarkeit Identischer, nicht das der Identität Ununterscheidbarer. Betrachten wir dazu die Sätze:

Frank glaubt, dass der Mount Everest im Himalaya liegt.

Frank glaubt, dass der höchste Berg der Erde im Himalaya liegt.

Unter der Voraussetzung, dass Frank nicht weiß, dass der höchste Berg der Mount Everest ist, könnte nun der erste Satz wahr und der zweite falsch sein. Gerade dies dürfte aber laut Identitätsprinzip bei Ausdrücken, die denselben Gegenstand bezeichnen, nicht der Fall sein. Die Lösung dieser Schwierigkeit lautet, dass das Identitätsprinzip bei so genannten intensionalen Ausdrücken (zu denen eben auch „glauben, dass“ gehört) außer Kraft gesetzt ist. D. h. die Aussagen, in denen die Ersetzung vorgenommen wird, dürfen solche Ausdrücke nicht enthalten (siehe auch opaker Kontext).

Geht man von einer der ersten beiden Formulierungen des Identitätsprinzips aus, so würde man sagen: Eigenschaften wie „von Frank für im Himalaya liegend gehalten zu werden“ sind keine eigentlichen Eigenschaften der Dinge und dürfen daher auch nicht zur Unterscheidung von Mount Everest und höchstem Berg der Erde herangezogen werden.

Identität in der Informatik

In der Informatik ist der Unterschied zwischen identischen Speichern und gleichen Speicherwerten leichter erkennbar: Bezieht sich die Implementierung einer Variablen in Form einer Speicheradresse auf dieselbe Speicherzelle, so ist der Inhalt einer zweiten Referenz auf dieselbe Speicherzelle identisch, in einer anderen Speicherzelle befindet sich nur möglicherweise der gleiche Wert.

Eigenschaften der Identität

Die Identität ist eine zweistellige Relation, d. h. eine Beziehung zwischen zwei Dingen. Genauer ist sie eine Äquivalenzrelation, d. h. sie hat die folgenden Eigenschaften:

• Reflexivität: Alles ist mit sich selbst identisch.
• Symmetrie: Wenn A mit B identisch ist, so auch B mit A
• Transitivität: Ist A mit B identisch, und B mit C, so auch A mit C

Noch genauer lässt die Identitätsrelation sich bestimmen als die „feinkörnigste“ Äquivalenzrelation in einer Sprache. Das bedeutet, dass bei a = b für jede Äquivalenzrelation R gilt: a R b. Eine andere Äquivalenzrelation wäre beispielsweise „gleichschwer“. Es gilt also, dass, wenn a mit b identisch ist, a auch gleichschwer wie b ist. Dasselbe gilt für alle übrigen Äquivalenzrelationen (gleichgroß, gleichfarbig etc.).

Es kann gezeigt werden, dass diese letzte Eigenschaft der maximalen Feinkörnigkeit die Identitätsrelation in eindeutiger Weise charakterisiert. D. h. gibt es neben der Identitätsrelation eine weitere Äquivalenzrelation R* mit dieser Eigenschaft so gilt: a = b genau dann, wenn a R* b

Einführung der Identitätsrelation in formalen Systemen

Es gibt verschiedene Möglichkeiten, die Identitätsrelation in einem auf Prädikatenlogik basierenden formalen System einzuführen.

Im Fall von Prädikatenlogik zweiter Stufe (oder höher) kann die Identität direkt und allgemein definiert werden:

$a = b \equiv_{def} \forall F (F(a) \equiv F(b))$

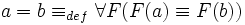
wobei F eine Prädikatvariable sein soll.

Diese Definition ist eine geradlinige Umsetzung des leibnizschen Identitätsprinzips.

Im Fall vom Prädikatenlogik erster Stufe kann eine Definition gegeben werden, wenn eine formale Theorie eine endliche Anzahl von nicht-definierten Prädikaten enthält. Betrachten wir dazu den Fall einer Mengentheorie mit dem Elementschafts-Prädikat 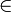$\in$ als einzigem undefinierten Prädikat. Dann ist die Identität wie folgt zu definieren: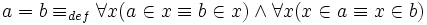

$a = b \equiv_{def} \forall x (a \in x \equiv b \in x) \wedge \forall x (x \in a \equiv x \in b)$

Bei mehreren Prädikaten müssten noch für diese entsprechende Klauseln hinzugefügt werden.

Im Fall von Prädikatenlogik erster Stufe gibt es jedoch keine allgemeine Definition, die unabhängig von den verwendeten Prädikaten wäre. Es gibt aber die Möglichkeit einer allgemeinen Einführung entweder über Regeln oder Axiome.

Durch Regeln lässt sich die Identität wie folgt einführen

Identitätsbeseitigung

Aus a = b und φ folgt φ^{a / / b}

(wobei φ^{a / / b} eine Formel ist, in der einige oder alle Vorkommen von „a“ durch „b“ ersetzt worden sind).

Identitätseinführung

Es gilt: a = a

Die Intuition hinter diesen Regeln ist, dass, wenn man gezeigt hat, dass a = b ist, man in jedem Satz in einem Beweis a (an einigen oder allen Stellen) durch b ersetzen kann. Ferner kann man in einem Beweis immer a = a setzen, da dies offenbar nie falsch ist.

Bei der axiomatischen Einführung setzt man das folgende Axiom-Schema (die so genannte Hao-Wang-Formel):

$\phi \equiv \forall b (a = b \supset \phi^{a//b})$,

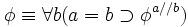Lies: φ ist genau dann wahr, wenn für alle b die Tatsache, dass b mit a identisch ist, bedingt, dass φ^{a / / b}. Das Axiom impliziert unmittelbar die Identitätsbeseitigung, aus ihm lässt sich jedoch auch sehr einfach die Identitätseinführung, a = a, ableiten.

Weblinks

• The Identity of Indiscernibles. Eintrag in der Stanford Encyclopedia of Philosophy (englisch, inklusive Literaturangaben)Vorlage:SEP/Wartung/Parameter 1 und weder Parameter 2 noch Parameter 3