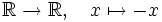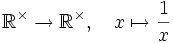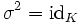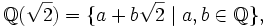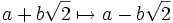- Selbstinvers
-
Der Begriff Involution bezeichnet in der Mathematik eine selbstinverse Abbildung. Die Bezeichnung leitet sich von dem lateinischen Wort involvere „einwickeln“ ab.
Inhaltsverzeichnis
Motivation
Eine lineare Abbildung
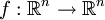 mit
mit 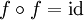 ist eine Spiegelung; im Fall n = 3 eine Spiegelung an einem Punkt, einer Geraden oder einer Ebene. Ersetzt man
ist eine Spiegelung; im Fall n = 3 eine Spiegelung an einem Punkt, einer Geraden oder einer Ebene. Ersetzt man  durch eine beliebige, nichtleere Menge und verzichtet auf die Linearität, dann erhält man den Begriff der Involution.
durch eine beliebige, nichtleere Menge und verzichtet auf die Linearität, dann erhält man den Begriff der Involution.Definition
Eine Abbildung
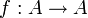 mit identischem Definitionsbereich und Zielbereich A heißt genau dann eine Involution, wenn für alle
mit identischem Definitionsbereich und Zielbereich A heißt genau dann eine Involution, wenn für alle 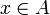 gilt:
gilt: 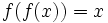 .
.Diese Forderung lässt sich auch kompakter formulieren als
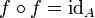 oder
oder 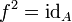 bzw.
bzw.- f = f − 1.
Dabei bezeichnet
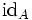 die Identität auf A.
die Identität auf A.Gelegentlich wird die Identität
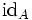 selbst nicht als Involution angesehen.
selbst nicht als Involution angesehen.Eigenschaften
- Jede Involution ist eine Bijektion und es gilt
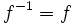 .
. - Ist π eine Bijektion der endlichen Menge
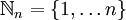 (also ein Element der symmetrischen Gruppe Sn), dann ist π genau dann involutorisch, wenn es sich als Produkt aus lauter disjunkten 2-Zyklen schreiben lässt.
(also ein Element der symmetrischen Gruppe Sn), dann ist π genau dann involutorisch, wenn es sich als Produkt aus lauter disjunkten 2-Zyklen schreiben lässt. - Eine Selbstabbildung
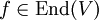 eines beliebigen Vektorraums V über einem Körper K ist genau dann involutorisch, wenn das Minimalpolynom von f die Form x2 − 1, x − 1 oder x + 1 hat. Das bedeutet: Ein involutorischer Endomorphismus ist stets diagonalisierbar, wenn K nicht die Charakteristik 2 hat, und alle seine Eigenwerte sind aus E = { − 1; + 1}.
eines beliebigen Vektorraums V über einem Körper K ist genau dann involutorisch, wenn das Minimalpolynom von f die Form x2 − 1, x − 1 oder x + 1 hat. Das bedeutet: Ein involutorischer Endomorphismus ist stets diagonalisierbar, wenn K nicht die Charakteristik 2 hat, und alle seine Eigenwerte sind aus E = { − 1; + 1}. - Über Körpern K mit der Charakteristik 2 gibt es nicht diagonalisierbare involutorische Endomorphismen. So ist im zweidimensionalen Vektorraum
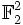 durch die Abbildung
durch die Abbildung 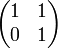 eine Involution gegeben, die nicht diagonalisierbar ist.
eine Involution gegeben, die nicht diagonalisierbar ist.
Beispiele
Negatives und Kehrwert
Die Abbildungen
und
sind Involutionen, denn es gilt
- − ( − x) = x für alle
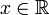
und
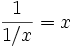 für alle
für alle 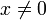 .
.
Ist allgemein G eine abelsche Gruppe, so ist die Abbildung
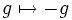 (bei additiver Schreibweise) bzw.
(bei additiver Schreibweise) bzw. 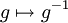 (bei multiplikativer Schreibweise) ein Gruppenautomorphismus und eine Involution. Für eine nichtabelsche Gruppe ist diese Abbildung zwar auch eine Involution, aber kein Gruppenhomomorphismus.
(bei multiplikativer Schreibweise) ein Gruppenautomorphismus und eine Involution. Für eine nichtabelsche Gruppe ist diese Abbildung zwar auch eine Involution, aber kein Gruppenhomomorphismus.Die komplexe Konjugation
Beim Rechnen mit komplexen Zahlen ist das Bilden der konjugiert-komplexen Zahl eine Involution: Für eine komplexe Zahl z = a + bi mit
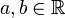 ist die konjugiert-komplexe Zahl
ist die konjugiert-komplexe Zahl 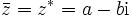 . Nochmalige Ausführung der Konjugation liefert
. Nochmalige Ausführung der Konjugation liefert 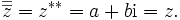
Das Transponieren von Matrizen
In der Menge
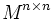 der quadratischen Matrizen über einer Menge M ist das Transponieren
der quadratischen Matrizen über einer Menge M ist das Transponieren 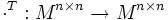 ,
, 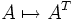 eine Involution.
eine Involution.Rechnen in F2
Im Restklassenkörper
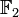 ist die Abbildung
ist die Abbildung 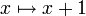 eine Involution:
eine Involution:- (x + 1) + 1 = x
Geometrie
In der Geometrie sind Punkt- und Geradenspiegelungen Involutionen.
Involutorische Chiffren
Involutorische Chiffren weisen die Eigenart auf, dass der Algorithmus zum Verschlüsseln und zum Entschlüsseln identisch ist. Sie sind damit besonders bequem zu handhaben. Ein einfaches Beispiel aus der Kryptologie ist die Verschiebechiffre ROT13, bei der zur Verschlüsselung jeder Buchstabe um den um 13 Stellen im Alphabet verschobenen Buchstaben ersetzt wird. Die zweimalige Anwendung dieser Methode ergibt eine Verschiebung um 26 Buchstaben und damit wieder den ursprünglichen Klartext. In der Geschichte gab es aber auch wesentlich komplexere involutorische Verschlüsselungsverfahren. Das wohl bekannteste Beispiel ist die deutsche Verschlüsselungsmaschine ENIGMA, die im Zweiten Weltkrieg im Nachrichtenverkehr des deutschen Militärs verwendet wurde.
Körperinvolution
Unter einer Körperinvolution versteht man üblicherweise eine Involution, die zugleich ein Körperautomorphismus ist.
Von einer Körperinvolution σ über einem Körper K fordert man also
sowie für alle
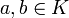
- σ(a + b) = σ(a) + σ(b)
und
- σ(ab) = σ(a)σ(b)
Die bekannteste nichttriviale Körperinvolution ist die Konjugation über den komplexen Zahlen. Aus diesem Grund benutzt man für eine Körperinvolution oft die gleiche Schreibweise wie für die komplexe Konjugation: Anstelle von σ(a) wird häufig
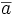 geschrieben.
geschrieben.Ein anderes Beispiel ist der Automorphismus des Körpers
der durch
definiert ist. Man beachte, dass er im Unterschied zur komplexen Konjugation den Betrag nicht erhält:
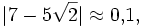 aber
aber 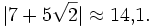
Wikimedia Foundation.