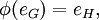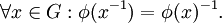Gruppenautomorphismus

In der Gruppentheorie betrachtet man spezielle Abbildungen zwischen Gruppen, die man Gruppenhomomorphismen nennt. Ein Gruppenhomomorphismus ist eine strukturerhaltende Abbildung zwischen Gruppen, und damit ein spezieller Homomorphismus.

Definition

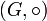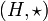Gegeben seien zwei Gruppen $(G, \circ)$ und $(H, \star)$. Eine Funktion 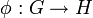$\phi: G\to H$ heißt Gruppenhomomorphismus, wenn für alle Elemente x, y von G gilt:

$\phi(x \circ y)$ = $\phi(x) \star \phi(y).$

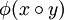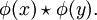
Die Gleichung besagt, dass der Homomorphismus strukturerhaltend ist: Es ist egal, ob man erst zwei Elemente verknüpft, und das Ergebnis abbildet, oder erst die zwei Elemente abbildet, und dann die Bilder verknüpft.

Aus dieser Definition folgt, dass ein Gruppenhomomorphismus das neutrale Element e_G von G auf das neutrale Element e_H von H abbildet, und dass er Inverse auf Inverse abbildet:

$\ \phi(e_G)=e_H,$

$\forall x\in G: \phi(x^{-1})=\phi(x)^{-1}.$

Bild und Kern

Als Bild (engl. image) des Gruppenhomomorphismus f: G → H bezeichnet man die Bildmenge von G unter f:

f(G) = Bild(f) = im(f) := { f(u) | u 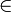$\in$ G },

Der Kern (engl. kernel) von f ist das Urbild des neutralen Elements e_H

f ⁻¹(e_H) = Kern(f) = ker(f) := { u 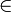$\in$ G | f(u) = e_H }.

Der Kern von f ist ein Normalteiler von G und das Bild von f ist eine Untergruppe von H.

Genau dann, wenn Kern(f) = {e_G} gilt (der Kern von f also nur das neutrale Element von G enthält, das immer im Kern liegt), ist f injektiv. Ein injektiver Gruppenhomomorphismus wird auch Gruppen-Monomorphismus genannt.

Beispiele

• Betrachte die additive Gruppe (Z, +) der ganzen Zahlen und die Faktorgruppe (Z/3Z, +) = {0, 1, 2}. Die Abbildung p: Z → Z/3Z, p(z) = z mod 3 = z + 3Z (siehe Kongruenz (Zahlentheorie) und Restklassenring), ist ein Gruppenhomomorphismus. Er ist surjektiv und sein Kern besteht aus der Menge 3Z aller durch 3 teilbaren ganzen Zahlen. Dieser Homomorphismus wird kanonische Projektion genannt.

• Die Exponentialfunktion ist ein Gruppenhomomorphismus zwischen der additiven Gruppe (R, +) der reellen Zahlen R und der multiplikativen Gruppe (R^*, ·) der reellen Zahlen ungleich 0, denn exp(x+y) = exp(x) exp(y). Diese Abbildung ist injektiv, und sein Bild ist die Menge der positiven reellen Zahlen.

• Die komplexe Exponentialfunktion ist ein Gruppenhomomorphismus zwischen den komplexen Zahlen C mit der Addition und den von 0 verschiedenen komplexen Zahlen mit der Multiplikation. Dieser Homomorphismus ist surjektiv und sein Kern ist ker(exp) = { 2πki : k in Z }, wie man z. B. aus der Eulerschen Identität entnehmen kann.

• Sind G und H beliebige Gruppen, dann ist die Abbildung h: G → H, die jedes Element auf das neutrale Element von H abbildet, ein Gruppenhomomorphismus. Sein Kern ist ganz G.

• Für jede Gruppe G ist die identische Abbildung id: G → G, id(x) = x, ein bijektiver Gruppenhomomorphismus.

Verkettung von Gruppenhomomorphismen

Sind h: G → H und k: H → K zwei Gruppenhomomorphismen, dann ist ihre Komposition k o h: G → K ebenfalls ein Gruppenhomomorphismus.

Die Klasse aller Gruppen bildet also mit den Gruppenhomomorphismen eine Kategorie.

Iso-, Endo-, Automorphismus

Ist ein Gruppenhomomorphismus h: G → H bijektiv, dann ist auch seine Umkehrfunktion ein Gruppenhomomorphismus, und h heißt dann Gruppenisomorphismus (siehe Isomorphismus), die Gruppen G und H heißen dann zueinander isomorph: Sie unterscheiden sich nur in der Bezeichnung ihrer Elemente und stimmen für fast alle Zwecke überein.

Ist h: G → G ein Gruppenhomomorphismus einer Gruppe in sich selbst, dann heißt er Endomorphismus. Ist er darüber hinaus bijektiv, dann heißt er Automorphismus. Die Menge aller Endomorphismen von G bildet mit der Komposition einen Monoid. Die Menge aller Automorphismen einer Gruppe G bildet mit der Komposition eine Gruppe, die Automorphismengruppe Aut(G) von G.

Die Automorphismengruppe von (Z, *) enthält nur zwei Elemente: Die Identität (1) und die Multiplikation mit −1; sie ist also isomorph zur zyklischen Gruppe C₂.

In der additiven Gruppe von Q ist jede lineare Abbildung f(x) = mx mit m ≠ 0 ein Automorphismus.

Homomorphismen zwischen abelschen Gruppen

Sind G und H abelsche (d. h. kommutative) Gruppen, dann bildet die Menge Hom(G, H) aller Gruppenhomomorphismen von G nach H selbst eine Gruppe, mit der „punktweisen Addition“:

(h + k)(x) := h(x) + k(x) für alle x in G.

Die Kommutativität von H benötigt man, damit h + k wieder ein Gruppenhomomorphismus ist.

Die Menge der Endomorphismen einer abelschen Gruppe G bildet mit der Addition eine Gruppe, die als End(G) bezeichnet wird.

Die Addition von Homomorphismen ist in folgendem Sinne verträglich mit der Komposition: Sind f in Hom(K, G), h, k in Hom(G, H), g in Hom(H, L), dann gilt

(h + k) o f = (h o f) + (k o f)   und    g o (h + k) = (g o h) + (g o k).

Dies zeigt, dass die Endomorphismengruppe End(G) einer abelschen Gruppe sogar einen Ring bildet, den Endomorphismenring von G.

Zum Beispiel ist der Endomorphismenring der Kleinschen Vierergruppe isomorph zum Ring der 2×2-Matrizen über dem Restklassenkörper Z/2Z.