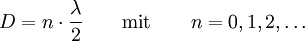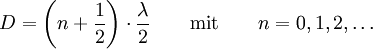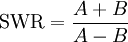Stehwelle

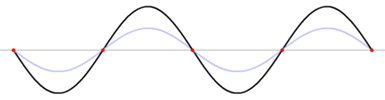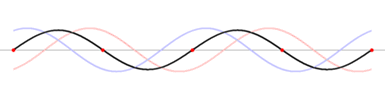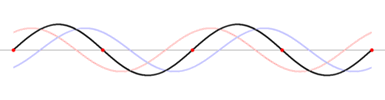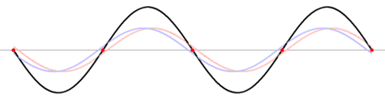
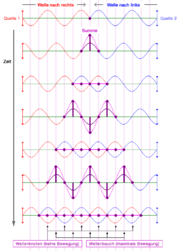
Eine stehende Welle (schwarz) als Überlagerung zweier Wellen; die Wellenknoten sind rot dargestellt. Skizziert sind einlaufende und auslaufende Welle in rot bzw. blau

Wellenreiter auf der stehenden Welle im Münchner Eisbach

Eine stehende Welle (im engeren Sinne) entsteht aus der Überlagerung zweier gegenläufig fortschreitender Wellen gleicher Frequenz und gleicher Amplitude. Ist die Amplitude nicht gleich, so bilden sich keine ortsfesten Knoten und Bäuche, folglich auch keine stehende Welle. Die Wellen können aus zwei verschiedenen Erregern stammen oder durch Reflexion einer Welle an einem Hindernis entstehen. Bei Wasserwellen siehe Clapotis.

Ein mechanisches Beispiel ist eine Seilwelle, bei der man ein Seilende auf und ab bewegt und so eine fortschreitende Welle im Seil erzeugt. Wird das andere Seilende befestigt, so wird die Welle an dieser Stelle reflektiert und läuft auf dem Seil zurück. Als Folge sieht man gar keine fortschreitende Welle mehr, sondern das Seil vollführt eine Schwingung, bei der bestimmte Stellen in Ruhe bleiben (Wellenknoten oder Schwingungsknoten), während andere mit großer Schwingungsweite (Amplitude) hin und her schwingen (Wellenbäuche oder Schwingungsbäuche).

Als stehende Welle wird auch eine Wasserwelle bezeichnet, die beständig an einer Stelle steht. Sie wird in Fließgewässern durch Hindernisse unter Wasser verursacht und unter anderem in Wildwassersportarten wie dem Wildwasserpaddeln (vor allem Kanurodeo) und von Wellenreitern genutzt.

Hintergrund

Entstehung einer stehenden Welle durch Überlagerung

Der Abstand zweier Wellenknoten bzw. zweier Wellenbäuche ist die halbe Wellenlänge der ursprünglichen fortschreitenden Welle. Da aber Energie transportiert wird - auch über den Knoten - ist immer eine zweite Größe vorhanden, deren Wellenknoten und Wellenbäuche um eine viertel Wellenlänge gegenüber der ersten Größe verschoben ist. Bei der Seilwelle ist das die Drehung des Seils: Dort wo ein Auslenkungsknoten vorhanden ist, ist ein Bauch der Drehung, wo der Bauch der Auslenkung ist, ist der Knoten der Drehung.

Wenn die stehende Welle mittels zweier gleichphasiger (synchron schwingender) Erreger erzeugt wird, befindet sich ein Wellenbauch genau in der Mitte zwischen ihnen, da die Wellen hier gleichzeitig eintreffen und sich stets gegenseitig verstärken. Eine Viertelwellenlänge hiervon entfernt beträgt die Zeitdifferenz des Eintreffens eine halbe Schwingungsperiode. Die Wellen sind hier gegenphasig und löschen sich aus, es entsteht ein Knoten. Durch Verallgemeinerung dieser Überlegung findet man die Bedingungen:

Bauch: Der Abstand D eines Schwingungsbauches vom Mittelpunkt ist ein halbzahliges Vielfaches der Wellenlänge.

$D = n \cdot \frac{\lambda}{2} \qquad \text{mit} \qquad n = 0, 1, 2, \dots$

Knoten: Der Abstand D eines Schwingungsknotens vom Mittelpunkt ist ein halbzahliges Vielfaches der Wellenlänge plus ein Viertel.

$D = \left(n + \frac{1}{2}\right) \cdot \frac{\lambda}{2} \qquad \text{mit} \qquad n = 0, 1, 2, \dots$

Die von der Welle transportierte Energie wird durch die Reflexion ebenfalls zurückgeworfen. Auf einem Wellenleiter mit (vollständig) stehender Welle kann daher keine Energie transportiert werden. Wird die Welle nur teilweise reflektiert, so resultiert eine stehende Welle, die von einer fortschreitenden überlagert wird. In diesem Falle ist noch Energietransport möglich.

Stehwellenverhältnis

Das Maß für den Grad der stehenden Welle auf einem Wellenleiter ist das Stehwellenverhältnis (englisch: standing wave ratio = SWR). Wenn A die Amplitude der hinlaufenden und B die der reflektierten Welle ist, so ist

$\mathrm{SWR} = \frac{A + B}{A - B}$

das Stehwellenverhältnis. Für A = B (vollständige Reflexion) ist es unendlich, für B = 0 (keine Reflexion) ist es 1. SWRs sind z.B. ein wichtiges Merkmal beim Energietransport von einem Funksender zur Antenne. Nur bei kleinem SWR wird die Sendeenergie zum großen Teil von der Antenne aufgenommen und abgestrahlt.

Um bei einem Wellenleiter die Reflexion zu vermeiden, muss er mit einem geeigneten Absorber abgeschlossen werden, im elektrischen Falle mit einem Abschlusswiderstand. Dieses kann der Verbraucher sein, dem die Energie zugeführt wird, oder ein ohmscher Widerstand, der die Energie in Wärme umwandelt. Letzteres spielt z. B. bei Datenleitungen in Computernetzen eine Rolle, bei der ein offenes Ende einer solchen Leitung mit einem Widerstand abgeschlossen werden muss (siehe: Impedanzanpassung), damit die reflektierten Signale nicht den Datentransport stören.

Man erhält eine stehende Welle im erweiterten Sinne, wenn man die Beschränkung auf eine Dimension fallen lässt. Dann ergibt sich zwischen zwei Wellenerregern eine stehende Welle, die sich räumlich verteilt. Man spricht dann allerdings nicht mehr von einer stehenden Welle, sondern von einem Interferenzmuster. Auf der Verbindungslinie zwischen den Erregern verhält es sich wie eine stehende Welle, jedoch sind ihre Knoten und Bäuche nun in den Raum fortgesetzt zu Interferenzminima (Knotenflächen) und Interferenzmaxima. Für die Bäuche (Maxima) gilt jedoch (bei Gleichphasigkeit der Erreger) immer noch die Bedingung 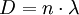$D = n \cdot \lambda$. Für die Knoten (Minima) gilt weiterhin 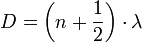$D = \left(n + \frac{1}{2}\right) \cdot \lambda$. Die Knotenflächen und Bauchflächen sind Hyperboloide, da eine Hyperbel gerade die geometrische Ortslinie aller Punkte ist, die von zwei festen Punkten eine konstante Abstandsdifferenz haben.

Visualisierung einer stehenden akustischen Welle in einem beschallten, mit Styroporkügelchen gefüllten Glasrohr im Dynamikum

Anwendung

• Hohlleiter
• Quantenmechanische Erklärung des Wasserstoffatoms
• Musikinstrumente, die den Resonanz-Effekt nutzen (Saiteninstrumente, Flöten, Orgelpfeifen, etc.) Bei fast allen Musikinstrumenten bilden sich stehende Wellen. In Konzertsälen wird nach Möglichkeit vermieden, dass Resonanzen und stehende Wellen auftreten. Hier wird auf eine für alle Frequenzen gleichmäßig hohe Dämpfung Wert gelegt.
• Für Laser: ein Optischer Resonator stabilisiert die Wellenlänge („Farbe“) des Laserlichts

Weblinks

• Auswirkung Stehende Welle auf Raumakustik (Beispielrechnung & Grafik)