Stoßantwort

Die Impulsantwort, auch Gewichtsfunktion genannt, ist das Ausgangssignal eines Systems, bei dem am Eingang ein Dirac-Impuls zugeführt wird. Sie wird in der Systemtheorie zur Charakterisierung linearer, zeitinvarianter Systeme benutzt. Der (ideale) Dirac-Impuls wird deshalb gerne für theoretische Betrachtungen verwendet, da er ein großes Frequenzspektrum besitzt und das invariante Element der Faltung darstellt. Bei der experimentellen Analyse werden Systeme dagegen häufig mit der Sprungfunktion angeregt und die Sprungantwort gemessen, die das Übertragungsverhalten eines solchen Systems ebenfalls vollständig beschreibt. Dadurch vermeidet man es, einen Dirac-Impuls mit guter Näherung erzeugen zu müssen, wofür das Eingangssignal kurzzeitig einen sehr hohen Wert annehmen müsste.

Es gilt: 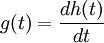$g(t) = \frac{{dh(t)}}{{dt}}$ Die Impulsantwort g(t) ist die Ableitung der Sprungantwort h(t).

Im Fall diskreter Signale ist das System ein linearer digitaler Filter. Das Dirac-Impuls-Signal ist ebenfalls das Eins-Element der diskreten Faltung, repräsentiert jedoch hier den Frequenzbereich [-π,π], entsprechend der Nyquist-Frequenz.

Mit Hilfe der Impulsantwort lässt sich ein System charakterisieren und z. B. dessen Frequenzgang oder Übertragungsfunktion bestimmen. Diese ist bei streng stabilen Systemen die Fourier-Transformierte der Impulsantwort.

Wird also ein Dirac-Impuls auf ein unbekanntes System gegeben, so lässt sich aus der Impulsantwort durch Fourier-Analyse, speziell durch die Laplace-Transformation, der Frequenzgang des unbekannten Systems ermitteln. Umgekehrt kann die Wirkung des Systems durch Faltung mit der Impulsantwort im Zeitbereich oder durch Multiplikation mit der Übertragungsfunktion im Frequenzbereich bestimmt werden.

Praktische Anwendung findet dieses Prinzip in jüngster Zeit in einigen DirectX- und VST-Plugins (siehe Faltungshall), die jegliches akustische System (Räume, Geräte, Mikrofone,...) virtuell nachbilden können. Zur Gewinnung der Impulsantwort wird dabei ein Signal, das hinreichend einem Dirac-Impuls ähnelt (also ein möglichst kurzer "Knall"), im Rechner generiert und (bei Räumen und Mikrofonen über Soundkarte, Verstärker und Lautsprecher, bei Geräten direkt) auf das System gegeben und seine Antwort (bei Räumen über ein günstig postiertes Mikrofon, bei Geräten und Mikrofonen direkt) aufgenommen. Bei der Ermittlung des Frequenzgangs kann es zu Verzerrungen kommen. Gründe sind vor allem Nichtlinearitäten (Klirrfaktor) und Rauschen.

Daher werden heute für akustische Messungen (fast) nur noch Methoden verwendet, welche die Impulsantwort nachträglich aus einer Messung mit einem breitbandigem (Pseudo)-Rauschsignal berechnen. Hierfür wird meist entweder ein Maximum Length Sequence Signal mit nachfolgender Kreuzkorrelation oder eine sogenannte Dual-FFT Messung, also der Vergleich der Spektren des Anregungs- und des Ausgangssignals, verwendet.

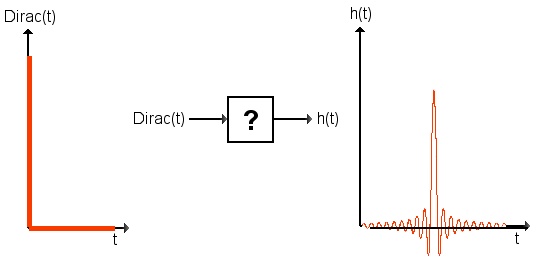
Hier das Beispiel eines Dirac-Impulses als Eingangssignal Dirac(t) für ein System mit unbekannter Übertragungsfunktion und die daraus resultierende Impulsantwort g(t) (hier eine (zeitlich beschnittene) Sinc-Funktion, die auf ein Tiefpass-Filter hindeutet).

Weblinks

• Anwendungsbeispiel: Impulsantwort bei Lautsprechern (inkl. Grafik)