Zeitgleichung

Als Zeitgleichung wird die Differenz zwischen der wahren Sonnenzeit (wahre Ortszeit WOZ) und der mittleren Sonnenzeit (mittlere Ortszeit MOZ) eines Ortes (oder Orten auf demselben Längengrad) bezeichnet.

Die Differenz zwischen Orts- und Zonenzeit heißt Zeitverschiebung.

In der älteren Literatur wird die umgekehrte Differenz, also zwischen mittlerer Sonnenzeit und wahrer Sonnenzeit, als Zeitgleichung bezeichnet. Daran ist noch die mittelalterliche Bedeutung von „Gleichung“ als „eine Korrektur zufügen“ zu erkennen:^[1] Man hatte der wahren Sonnenzeit die Differenz zur mittleren Sonnenzeit hinzuzufügen, um zu letzterer zu gelangen.

Die Zeitgleichung wird verursacht

1. durch die elliptische Form der Erdbahn: Zeitgleichungs-Anteil mit einer Periodendauer von etwa einem Jahr und
2. durch die Neigung der Erdachse auf ihrer Bahnebene: Zeitgleichungs-Anteil mit einer Periodendauer von etwa einem halben Jahr.

Eine einfache (nicht um die Zeitgleichung korrigierte) Sonnenuhr zeigt die WOZ an. Sie kann mehr als 16 Minuten (um den 3. November) gegenüber der MOZ vorgehen oder mehr als 14 Minuten nachgehen (um den 11. Februar). Einfache Sonnenuhren sind manchmal mit einem Zeitgleichungsdiagramm oder einer -Tabelle versehen, um dem Benutzer die Ermittlung der MOZ und damit schließlich der Zonenzeit (zum Beispiel der Mitteleuropäischen Zeit (MEZ)) zu ermöglichen.

Die Zeitgleichung ändert sich über lange Zeit geringfügig, sowohl in ihrer Kurven-Form, in ihrer Lage relativ zum Jahresdatum, als auch in ihren Extremwerten. Die abgebildete Jahres-Kurve ist mehrere Jahrzehnte lang verwendbar, wenn Änderungen im Sekundenbereich beim Gebrauch nicht stören. In astronomischen Jahrbüchern werden genauere, jährlich neu berechnete Werte angegeben.

Gegenwärtige Zeitgleichung in Minuten, abhängig vom Jahresdatum. Zusätzlich sind noch die (fiktiven) Teil-Zeitgleichungen zu sehen, wenn sich die Erde auf einer Kreisbahn bewegen würde, beziehungsweise wenn es keine Neigung der Erdachse gäbe.

Stern- und Sonnentag

Die sich drehende und um die Sonne kreisende Erde :
von 1 nach 2 = Bahnfahrt pro Sterntag
von 1 nach 3 = Bahnfahrt pro Sonnentag

Der Zeitraum zwischen zwei Meridiandurchgängen der Sonne ist ein Sonnentag; er beträgt im Mittel 24 Stunden. Im Unterschied dazu wird der Zeitraum zwischen zwei Meridiandurchgängen eines Fixsternes als Sterntag bezeichnet. Dies ist die Zeit für eine Drehung der Erde um sich selbst und beträgt 23 Stunden 56 Minuten und 4 Sekunden. Der Unterschied zwischen der Länge des Sterntages und der Länge des Sonnentages resultiert aus der jährlichen Bewegung der Erde um die Sonne. Während einer Tages-Umdrehung (Rotation) läuft die Erde auf ihrer Bahn um die Sonne fast einen Bogengrad weiter (360 Grad in 365 Tagen). Da beide Kreisbewegungen gleichen Drehsinn haben, muss sich die Erde um ebenfalls einen Grad über die volle Umdrehung hinaus weiterdrehen, bis die Sonne wieder durch den Meridian geht. Dies benötigt im Mittel etwa 4 Minuten.

Die mittlere Sonne

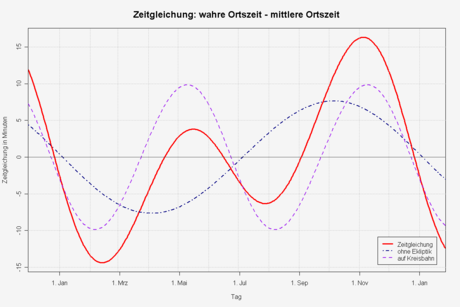
Die Eigendrehung der Erde ist ziemlich gleichmäßig, die Dauer des Sterntags kann als konstant angesehen werden. Ungleichmäßig lang ist allein die Zusatz-Zeit, die für die Zusatz-Drehung zum Ausgleich der täglichen Bahnfahrt der Erde benötigt wird. Sie kann bis etwa 30 Sekunden länger und bis etwa 20 Sekunden kürzer sein als ihr Mittelwert von knapp 4 Minuten. Weil die wahre Sonnenzeit mit leicht variabler Geschwindigkeit vergeht, wurde auf den Gebrauch der mittleren Sonnenzeit ausgewichen und damit ein gleichmäßiges Zeitmaß gewonnen. Die mittlere Sonne ist vorstellbar als eine künstliche Sonne, die gleichmäßig auf dem Himmels-Äquator umläuft (geozentrisch betrachtet). Den Unterschied zwischen Wahrer und mittlerer Sonnenzeit bezeichnet man als die Zeitgleichung. Da sich die Abweichungen des wahren Sonnentages vom mittleren Sonnentag jeweils über etwa drei Monate hinweg aufsummieren, bevor sie ihr Vorzeichen wechseln, kann die Zeitgleichung bis etwa eine Viertelstunde (+16/-14 Minuten, rote Linie in obenstehendem Diagramm) betragen.

Die Ursachen für die Zeitgleichung erkennt man leichter aus einer heliozentrischen Sicht, denn sie folgen aus den Bewegungen der Erde relativ zur ruhenden Sonne. Der Einfachheit halber wird weiterhin von „Sonnenzeit“ gesprochen, auch wenn es sich um Bewegungen der Erde in Abhängigkeit von der Zeit handelt.

Elliptizität der Erdbahn

Die Bahn der Erde um die Sonne ist eine Ellipse, in deren einem Brennpunkt die Sonne steht. Das zweite Keplersche Gesetz beschreibt die Veränderung der Bahngeschwindigkeit der Erde während eines Umlaufs. In der Umgebung des Perihels – dem sonnennächsten Punkt – bewegt sich die Erde schneller als im Mittel und legt während eines Tages eine größere Strecke zurück, so dass sie eine etwas größere Zusatzdrehung machen muss, bis die Sonne wieder im Süden steht. Das dauert länger als im Durchschnitt. In der Umgebung des Aphels ist es umgekehrt.

Im Winterhalbjahr beidseits des Perihels (etwa am 3. Januar) vergeht die wahre Sonnenzeit wegen der größeren Erdgeschwindigkeit (und der dadurch nötigen größeren Zusatzdrehung) langsamer, im Sommerhalbjahr beidseits des Aphels (etwa am 5. Juli) vergeht sie schneller als die gleichmäßige mittlere Sonnenzeit. Die Schwankung der wahren Tageslänge beträgt etwa ± 8 Sekunden^[2]. Die Summierung ergibt etwa ± 7½ Minuten jährliche Schwankung der wahren Sonnenzeit infolge Elliptizität der Erdbahn (sinus-förmige blaue Linie in oben stehendem Diagramm, Nulldurchgänge im Perihel und im Aphel, Start im Perihel/3.Januar).

Neigung der Erdachse

Die Erdachse steht nicht senkrecht auf der Ebene ihrer Bahn um die Sonne (im heliozentrischen Schema nicht senkrecht auf der Bildebene). Das ist die zweite Ursache der Zeitgleichung. Entscheidend ist dabei, dass die Richtung der Erdachse gegen den Fixsternhimmel nahezu konstant ist, sich aber gegen die Verbindungslinie Erde-Sonne täglich ändert. Die Bahnebene schneidet die Erde nicht im Äquator, sondern in einer dazu geneigten Ebene. Die Achse für die erforderliche tägliche Zusatzdrehung ist eine Parallele zur Bahnachse. Die Tageszeit wird aber von der gleichmäßigen Drehung der Erde um die eigene Achse bestimmt.

An den Tag-und-Nacht-Gleichen schneiden sich die beiden Achsen maximal unter dem Ekliptikwinkel ε. Der Winkel zwischen beiden Ebenen ist jetzt am größten (etwa 23,44°). Die Drehung der Erde um ihre Achse wirkt sich mit maximaler Verstärkung als Drehung um die Parallele zur Bahnachse aus. Folge ist, dass die erforderliche Zeit für die Zusatzdrehung kleiner als im Mittel ist. Die wahre Sonnenzeit vergeht schneller als die mittlere Sonnenzeit.

An den Sonnenwenden befinden sich beide Achsen in einer Ebene. Die Zusatzdrehung bildet sich als Bogen auf einem der beiden Wendekreise ab. Der zugehörende Bogen auf dem Äquator ist größer. Die erforderliche Zusatzdrehung der Erde um ihre Achse ist größer als im Mittel. Die wahre Sonnenzeit vergeht langsamer als die mittlere Sonnenzeit.

Diese zweite Ursache der Zeitgleichung alleine bewirkt eine Schwankung des wahren Tages von etwa ± 20 Sekunden^[2]. Die Summierung ergibt knapp ± 10 Minuten halbjährliche Schwankung der wahren Sonnenzeit infolge Neigung der Erdachse (sinus-förmige Magenta-farbene Linie in oben stehendem Diagramm, Nulldurchgänge an den Tagen der Sonnenwenden und der Tag-und-Nacht-Gleichen, Start zur Wintersonnenwende).

Zeitgleichung

Die Wirkungen der Elliptizität der Erdbahn und der Neigung der Erdachse überlagern sich und ergeben die Zeitgleichung (rote Linie in obigem Diagramm). Da beide sinusförmige Kurven zeitlich leicht gegeneinander verschoben sind, sind die Extremwerte im Ergebnis kleiner als die Summe beider Einzelextremwerte. Die Zeitgleichung hat gegenwärtig folgende Kennwerte:

• 4 Nullpunkte: 15. April, 13. Juni, 1. September und 25. Dezember,
• 2 Hauptextremwerte: um den 11. Februar (gegenwärtig −14 min 14 s) und um den 3. November (gegenwärtig +16 min 26 s),
• 2 Nebenextremwerte: um den 14. Mai (gegenwärtig +3 min 41 s) und um den 25. Juli (gegenwärtig −6 min 32 s).

Berechnung in astronomischen Jahrbüchern

Es folgt die Berechnung, wie sie in astronomischen Jahrbüchern vorgenommen wird. Man ermittelt relativ genaue Werte für beliebig viele Momente in der Zukunft (in der Regel von Tag zu Tag). Diese wiederholen sich nicht streng mit der Periode eines Jahres, denn die Jahrlänge kann nicht mit einer ganzen Zahl von Tagen angegeben werden. Da sich einige sogenannte Jahreskonstanten zudem langsam ändern, wird die Rechnung in der Regel in jedem Jahr neu durchgeführt.

Die Darstellung nimmt ihren Ausgang von den Arbeiten Keplers, der sogenannten Kepler-Gleichung.^[3]

Geozentrisch: Differenz zweier Rektaszensionen

Definition:

$\mathrm{ZG} = \mathrm{WOZ} - \mathrm{MOZ} \quad [\mathrm{min}]$.

Als „Macher“ der MOZ wurde die mittlere Sonne eingeführt.
Die Zeitgleichung ist proportional zur Differenz zwischen den Rektaszensionen der mittleren (α_M) und der wahren Sonne (α):

$\text{ZG} = 4 (\alpha_M - \alpha) \quad [\text{min}]$

Der Faktor 4 ergibt sich daraus, dass zwei Himmelskörper mit 1° Rektaszensionsdifferenz die Meridianebene 4 min nacheinander passieren. Die Reihenfolge der beiden Subtraktionsterme hat sich umgekehrt, weil die Richtungen für Stundenwinkel τ (ihm entspricht die Tageszeit) und Rektaszension α gegensätzlich vereinbart sind.

Die Tageszeit, insbesondere die auf einem bestimmten Längengrad gültige WOZ oder MOZ kann außer Acht bleiben. In der folgenden Betrachtung erstreckt sich der Zeitraum mindestens über ein Jahr. Der gleichmäßige Ablauf der Zeit wird mit der mittleren Anomalie dargestellt.

Heliozentrisch: Wahre Anomalie (Wahre Erde auf elliptischer Bahn)

Während sich die Erde auf ihrer Bahn vorwärts bewegt, rotiert ein von der Sonne zur Erde zeigender Vektor um die Sonne. Sein mit der Geraden zwischen Sonne und Ort des Perihels gebildeter Winkel heißt wahre Anomalie V(t). Analog dazu lässt sich eine mittlere Anomalie M(t) angeben. Dabei handelt es sich um einen Vektor, der gleichmäßig um die Sonne rotiert. Er ist als Vektor vorstellbar, der zu einer fiktiven Erde zeigt, die sich mit konstanter Winkelgeschwindigkeit auf der Bahnellipse bewegt.

$M(t) = M_0 + \frac{360^\circ}{J_{\text{an}}} \cdot t$.

J_an ist das anomalistische Jahr (Zeit für zwei aufeinander folgende Passagen des Perihels). Weil die Anomalien im Perihel Null sind, die Zeitgleichung aber mit t = 0 am etwa 3 Tage früherem Jahresanfang aufgestellt wird, ist die Winkeldifferenz M₀ zwischen Perihel und dem Ort der Erde am 1. Januar, 0 Uhr zu addieren (M₀ ist negativ). M₀ ist eine Jahreskonstante mit deutlich vier verschiedenen Werten gemäß Schaltjahr-Zyklus.

Das Verhältnis der beiden Anomalien zueinander ist ein Maß für den Teil der Zeitgleichung, der aus der Elliptizität folgt. Die Beziehung zwischen beiden folgt aus dem Bewegungsgesetz der elliptischen Bahnfahrt, dem zweiten Keplerschen Gesetz. Kepler hat den Zusammenhang schon mit Hilfe der später sogenannten Kepler-Gleichung formuliert. Der Ort der wahren Erde wird zunächst von der gemäß Kepler sogenannten exzentrischen Anomalie E(t) repräsentiert. Sie ist wie die beiden anderen Anomalien ein auf das Perihel bezogenes Winkelmaß. Der zugehörige Vektor geht nicht von der Sonne, sondern vom Mittelpunkt der Ellipse aus. Er zeigt zu einem Hilfspunkt auf dem Umkreis zur Ellipse. Die Kepler-Gleichung lautet mit der relativen (numerischen) Exzentrizität e der Ellipse:

$M(t)=E(t)-\frac{180^\circ}{\pi} \cdot e \cdot \sin E(t)$.

Sie ist nach E(t) aufzulösen, was in geschlossener Form nicht möglich ist, aber zum Beispiel mit dem numerischen Verfahren gelingt, das Newton anlässlich dieser Aufgabe entwickelte.

Mit dem Ergebnis E(t) = f(M(t)) lässt sich nun die wahre Anomalie V(t) bei vorgegebener mittleren Anomalie M(t) (beziehungsweise als Funktion der gleichmäßig ablaufenden Zeit) mit Hilfe rein geometrischer Betrachtung in der Ellipse und in ihrem Umkreis angeben:

$\tan\left(\frac{V(t)}{2}\right) = \kappa \cdot \tan\left(\frac{E(t)}{2}\right)$.

$\textstyle \kappa = \sqrt{\frac{1+e}{1-e}}$ ist eine Ellipsenkonstante.

Die erste Ursache der Zeitgleichung ist hiermit erfasst.

Übergang zur geozentrischen Sicht

Die Anomalie V(t) der Wahren Erde ist in die Rektaszension α(t) der Wahren Sonne umzuwandeln. Der Weg dort hin führt über die ekliptikale Länge Λ der Wahren Sonne, denn die (kreisförmige) Ekliptik am geozentrischen Himmel entspricht der (elliptischen) Erdbahn. Die ekliptikale Länge ist in die in der Zeitgleichung gebrauchte auf dem Himmelsäquator gemessene Rektaszension umzurechnen. Denn die Tageszeit wird durch den täglichen scheinbaren Umlauf der Sonne bestimmt, der auf dem Himmelsäquator oder auf zu diesem parallelen Kreisen stattfindet.

Der Übergang zum geozentrisch üblichen Bezugspunkt, dem Frühlingspunkt kann bereits auf der Ellipse erfolgen. Die Differenz zwischen Perihel und Frühlingspunkt sei:

$L(t) = L_0 + \frac{\text{pf}}{J_\text{tr}} \cdot t$

Der mit der Zeit veränderliche Summand ist sehr klein. Er berücksichtigt, dass sich Frühlingspunkt und Perihel sehr langsam mit etwa $\tfrac{0{,}017^\circ}{J_\text{tr}}$ nähern. J_tr ist das tropische Jahr (Zeit für zwei aufeinander folgende Passagen des Frühlingspunkts). L₀-Werte sind Jahres-Konstanten, die sich von Jahr zu Jahr gering durch die inzwischen erfolgte Näherung unterscheiden.

Aus V(t) = Λ(t) − L(t) wird:

$\Lambda(t) = V(t) + L(t) \qquad (L(t) \text{ ist negativ})$.

Geozentrisch: Rektaszension der Wahren Sonne

Die Umrechnung zwischen ekliptikalen und äquatorialen Koordinaten ist z.B. mit den bekannten Transformations-Gleichungen oder mit folgender einfachen Beziehung im entsprechenden rechtwinkligen sphärischen Dreieck möglich:

$\alpha(t) = \arctan ( \tan \Lambda(t) \cdot \cos \varepsilon )$.

ε ist der Winkel zwischen Ekliptik- und Äquatorkreis (die Schiefe der Ekliptik): $\varepsilon = 23{,}44^\circ$.

Mit dem „Herunterholen“ der wahren Sonne auf den Äquator ist außer der ersten auch die zweite Zeitgleichungs-Ursache berücksichtigt.

Geozentrisch: Mittlere Rektaszension

In der Zeitgleichung wird der ungleichmäßige Rektaszensions-Zuwachs der Wahren Sonne mit dem gleichmäßigen der fiktiven mittleren Sonne verglichen. Letzterer hat folgende Gleichung.

$\alpha_M(t) = \alpha_0 + \frac{360^\circ}{J_\text{tr}} \cdot t$.

α_M(t) ist zu jeder Zeit gleich der ekliptikalen Länge Λ(t) der fiktiven Erde, die die mittlere Anomalie M(t) repräsentiert,^[4] weil die fiktive mittlere Sonne gemäß Definition den Frühlingspunkt gleichzeitig mit der fiktiven Erde passiert.

Beide sich gleichmäßig bewegenden fiktiven Körper legen zwischen t = 0 (Jahresanfang) und dem Zusammentreffen am Frühlingspunkt einen Bogen derselben Länge α₀ zurück. Für die fiktive Erde beträgt dieser Bogen M₀ + L(t). Dabei ist L(t) die ekliptikale Länge des Perihels im Moment t = 0. Also ist α₀ = M₀ + L₀, die Summe der beiden schon benutzten Jahreskonstanten. Damit folgt:

$\alpha_M(t) = M_0 + L_0 + \frac{360^\circ}{J_\text{tr}} \cdot t$.

Zur Erinnerung: M₀ und L₀ haben negative Werte.

Wegen der oben genannten Gleichheit kann im folgenden sowohl mit α_M(t) als auch mit Λ(t) gearbeitet werden:

Λ(t) = L(t) + M(t).

Stundenschleife (Analemma) eines Mittagsweisers für MOZ,
darüber eine einfache Sonnenuhr (mit Stundengeraden für WOZ)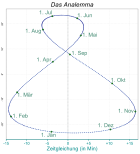

Analemma, gegenwärtig

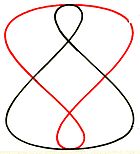Analemma, im Jahr 1246, schematisch, schwarze Figur

Analemma, im Jahr 6433, schematisch, schwarze Figur

Rechenergebnis

Mit den beiden Teilgleichungen α(t) und α_M(t) werden mit der Zeitgleichung in der Form

$\text{ZG}(t) = 4 \cdot (\alpha_M(t) - \alpha(t)) \quad [\text{min}]$

Werte für beliebig viele Momente in der Zukunft (in der Regel von Tag zu Tag) ausgerechnet.

Weil die Jahreskonstante M₀ innerhalb eines Schaltjahrzyklus deutlich variiert, werden aber mindestens vier Zeitgleichungen berechnet. Nach vier Jahren kann man in erster Näherung die für die vier Vorjahre errechneten Werte benutzen.

Die Jahreskonstante M₀ und genaue Werte für die sehr langsam veränderlichen Basis-Werte L₀, e, ε, J_tr und J_an werden in astronomischen Jahrbüchern angegeben.^[5]

Analemma

Trägt man die Zeitgleichung über die Deklination (vertikale Achse) der Sonne auf, entsteht eine Figur, die als Analemma bezeichnet wird. Die leichte Asymmetrie zwischen rechts und links rührt davon her, dass Perihel und Wintersonnenwende nicht auf denselben Tag fallen. Letzteres war im Jahre 1246 der Fall (Tag der Wintersonnenwende etwa wie heute). Die innere Schnittstelle galt etwa für den 16. April und den 29. August (Gregorianischer Kalender rückwärts angewendet).

Im Jahre 6433 werden Perihel und Frühling-Äquinoktium zusammenfallen. Die Zeitgleichung wird am Tag beider Äquinoktien null und das Analemma eine zu diesen Punkt symmetrische Figur sein.^[6]

Am häufigsten ist das Analemma als Stundenschleife auf Sonnenuhren zu sehen, die zur Anzeige der mittleren Sonnenzeit ausgelegt sind. Oftmals wird es allerdings in zwei Teile (ein Teil ähnlich einem S, der andere ähnlich einem Fragezeichen) aufgeteilt, um Verwechslungen beim Ablesen zu verhindern (für einen Deklinationswert gibt es zwei Punkte auf der ganzen Figur). Jedes der beiden Teile gilt etwa ein halbes Jahr lang. Solche Uhren haben zwei auswechselbare Zifferblätter. Die Zifferblätter lassen sich leicht auf die am Aufstellort gültige Zonenzeit auslegen, zeigen also die „Normalzeit“ an.

Auch die jeden Tag zur gleichen mittleren Zeit fotografierte Sonne ergibt in der Summe ein am Himmel stehendes Analemma.^[7]

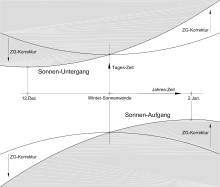Verschiebung der Sonnenauf- und -untergangszeiten zur Winter-Sonnenwende, schematisch

Sonnenauf- und -untergang zur Wintersonnenwende

Zur Zeit der Sonnenwenden kehrt sich die Veränderung in der Mittagshöhe der Sonne und in ihren täglichen Momenten des Sonnenaufgangs und des Sonnenuntergangs um. Vor und nach der Umkehr sind die täglichen Veränderungen klein, dazwischen sind sie 0. In den Zeiten beider Sonnenwenden, besonders aber zur Zeit der Wintersonnenwende geht die wahre Zeit gegenüber der Mittleren Zeit (Normalzeit) von Tag zu Tag deutlich zu langsam. Im Winter sind es fast 30 Sekunden, mit denen sich zum Beispiel der in Normalzeit angegebene Sonnenaufgang täglich verspätet, obwohl er sich mit wahrer Zeit gemessen kaum oder gar nicht verändert. Erst Anfang Januar beginnt der wahre Sonnenaufgang täglich um mehr als 30 Sekunden früher stattzufinden. Die mit Normalzeit gemessene Umkehr des Sonnenaufgangs verschiebt sich auf Anfang Januar. Der Sonnenuntergang wird in Normalzeit auch bis fast 30 Sekunden später als der wahre Sonnenuntergang angezeigt. Das bedeutet, dass seine mit Normalzeit gemessene Umkehr früher, bereits Mitte Dezember erfolgt. Auf den kürzesten Tag wirkt sich das nicht aus. Er bleibt der mittlere Tag zwischen den gegenseitig verschobenen Umkehr-Momenten am Morgen und am Abend, nämlich der 21. oder der 22. Dezember. Viele Menschen registrieren das längere Tageslicht am Abend bereits ab Mitte Dezember und meinen, die Tage würden schon länger. Dass sie sich in der Summe täuschen, liegt daran, dass der Sonnenaufgang weniger intensiv als der Untergang beobachtet wird.

Zur Zeit der Sommersonnenwende ist die tägliche Verspätung der wahren Zeit nur etwa 10 Sekunden, also nicht so deutlich wie im Winter.

Historisches

Die Zeitgleichung war schon den antiken Astronomen bekannt. Geminus erwähnt sie.^[8] Im Almagest des Ptolemäus wurde sie ziemlich genau und bündig angesprochen.^[9] Die heute verwendete quantitative Beschreibung der Zeitgleichung hat John Flamsteed schon 1672, also bald nach Bekanntwerden der Keplerschen Gesetze, vorgenommen.^[10][11]

In älteren Jahrbüchern findet sich die Zeitgleichung mit umgekehrtem Vorzeichen. Der Wortteil Gleichung bedeutete im Mittelalter eine Korrektur zufügen.^[1] Man hatte der wahren Sonnenzeit die Werte der Zeitgleichung zu addieren, um auf die mittlere Zeit zu kommen.

Heutzutage liest man die mittlere Zeit von den (stets gleichmäßig laufenden) Uhren ab und addiert ihr die Werte der Zeitgleichung, um die wahre Sonnenzeit zu erhalten, die zum Beispiel eine einfache Sonnenuhr anzeigen muss. In den französischen Jahrbüchern ist die alte Konvention noch üblich.^[12]

Literatur

• Hughes, D. W., Yallop, B. D., Hohenkerk, C. Y.: The Equation of Time, Mon. Not. R. astr. Soc. (1989), 238, 1529–1535 [3]
• Bernd Loibl: Wann ist Mittag?. In: Sterne und Weltraum Sterne und Weltraum, Spektrum der Wissenschaft, 8–9/1996. S. 643–645
• Robert Weber. Zeitsysteme. In: Hermann Mucke (Hrsg.): Moderne astronomische Phänomenologie. 20. Sternfreunde-Seminar, 1992/93. Planetarium der Stadt Wien – Zeiss Planetarium der Stadt Wien – Zeiss Planetarium und Österreichischer Astronomischer Verein 1992, S. 55–102 (weblink, 15. Apr 2006)

Weblinks

 Commons: Equation of time (sundials) – Sammlung von Bildern, Videos und Audiodateien

• http://www.zum.de/Faecher/Materialien/gebhardt/astronomie/zeitglei.html, qualitative Behandlung mit Bildern
• http://www.waa.at/hotspots/zeitgleichung/wintersonne.html, qualitative Behandlung, gute Erklärung
• http://lexikon.astronomie.info/zeitgleichung/, Näherungs-Formel
• http://www.swetzel.ch/sonnenuhren/zgel/zgel.html, elementare Behandlung → Jahresgleichung als Summe aus 2 Sinusfunktionen
• http://www.swetzel.ch/sonnenuhren/zgna/zgna.html, klassische Behandlung → keine Jahresgleichung
• http://www.schulphysik.de/strutz/zeitgl.pdf, mit Mathematik (Reihenentwicklungen) → Jahresgleichung als Summe aus 4 Sinusfunktionen
• http://info.ifpan.edu.pl/firststep/aw-works/fsII/mul/mueller.html, anspruchsvolle mathematische Behandlung (Differential- und Integralrechnen) → Jahresgleichung als Summe aus 10 Sinusfunktionen

Einzelnachweise

1. ↑ ^{a b} Siehe N. Dershowitz, E.M. Reingold: Calendrical Calculations, Cambridge University Press, 2008, ISBN 978-0-521-70238-6, Seite 182
2. ↑ ^{a b} Siegfried Wetzel Die Zeitgleichung, elementar behandelt - DGC-Mitteilungen Nr.109, 2007
3. ↑ Die Formel-Zeichen sind die gleichen wie im Sonnenuhren-Handbuch, Berechnung der Zeitgleichung, Deutsche Gesellschaft für Chronometrie e.V., Fachkreis Sonnenuhren, 2006, S. 43–49
4. ↑ Sonnenuhren-Handbuch, Berechnung der Zeitgleichung, Deutsche Gesellschaft für Chronometrie e.V., Fachkreis Sonnenuhren, 2006, S. 46
5. ↑ zum Beispiel bis zum Jahr 2025 im Sonnenuhren-Handbuch, Deutsche Gesellschaft für Chronometrie e.V., Fachkreis Sonnenuhren, 2006, S. 48
6. ↑ Heinz Schilt: Zur Berechnung der mittleren Zeit für Sonnenuhren, Schriften der Freunde alter Uhren, 1990
7. ↑ Am Himmel in Griechenland fotografierte Analemmata [1]
8. ↑ O. Neugebauer: A History of Ancient Mathematical Astronomy, Berlin 1975
9. ↑ R. Wolf: Handbuch der Astronomie, Amsterdam 1973
10. ↑ Flamsteed eröffnete seine Laufbahn mit einer wichtigen Abhandlung über die Bestimmung der Zeitgleichung. [2]
11. ↑ Flamsteed J.: De inaequilitate dierum solarium dissertatio astronomica. London 1672. (online)
12. ↑ J. Meeus: Astronomical Algorithms, Richmond 2000, S. 184

 Wiktionary: Zeitgleichung – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen