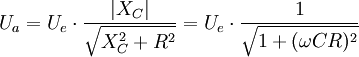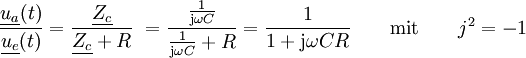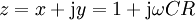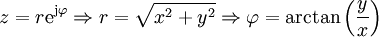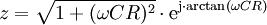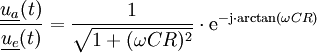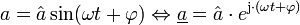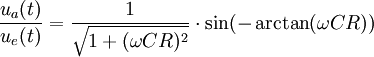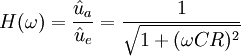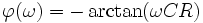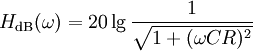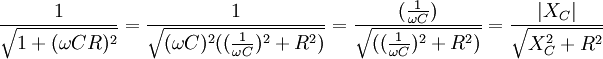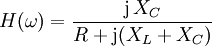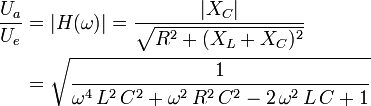Tiefpassfilterung

Als Tiefpass bezeichnet man in der Elektronik Filter, die Signalanteile mit Frequenzen unterhalb ihrer Grenzfrequenz annähernd ungeschwächt passieren lassen, Anteile mit höheren Frequenzen dagegen abschwächen. Entsprechende Filterfunktionen können aber auch in anderen Bereichen, wie zum Beispiel Mechanik, Akustik oder Hydraulik vorkommen, sie werden dort meist jedoch nicht so genannt.

Anwendung

Tiefpässe für schwache Signale können entweder in analoger Technik aus Widerständen, Spulen und Kondensatoren aufgebaut sein und zur Verbesserung ihrer Filterfunktion aktive Bauelemente wie Transistoren enthalten. Sie können aber auch – wie andere Filterfunktionen – durch Computerprogramme nachgebildet werden und spielen in der digitalen Signalverarbeitung und in der Computergrafik (Anti-Aliasing) eine Rolle.

Tiefpässe für starke Signale und für Leistungsübertragung können sinnvoll nur in analoger Technik aus Kondensatoren und Spulen aufgebaut werden. Hauptanwendung ist die Hochfrequenztechnik, man findet sie auch an den Lastausgängen von Frequenzumrichtern, Klasse-D-Verstärkern, Schaltnetzteilen und in Netzfiltern.

Tiefpass-Filter in der Niederfrequenztechnik werden anwendungsbezogen auch als Höhensperre, Höhenfilter, Treble-Cut-Filter, High-Cut-Filter, oder Rauschfilter bezeichnet. Diese Begriffe sind in der Tontechnik gebräuchlich; sie weisen darauf hin, dass ein solches Filter, zum Beispiel in einem Equalizer, die „Höhen“ des Signals bzw. das Rauschen abschwächt, das vorwiegend hohe Frequenzen enthält; siehe auch Entzerrung (Tontechnik). Tiefpässe werden den Tieftonlautsprechern in Lautsprecherboxen bzw. Subwoofern vorgeschaltet.

Tiefpassfunktionen kommen auch in der Mechanik (Schwingungsdämpfung), Akustik (die Schallausbreitung tiefer Frequenzen ist verlustärmer), Optik (Kantenfilter), Hydraulik oder der Lichtausbreitung in der Atmosphäre vor, werden dort jedoch nicht so genannt.

Eine Sonderstellung eines Tiefpassfilters nimmt der ideale Tiefpass ein. Dieser Tiefpass weist eine nicht kausale Übertragungsfunktion auf und kann daher in Praxis nicht realisiert werden. Er dient wegen seiner einfachen Übertragungsfunktion in der Filtertheorie als vereinfachtes Modell. Reale Tiefpässe können sich nur möglichst gut der Eigenschaft des idealen Tiefpasses annähern.

Mit Hilfe von Filter-Transformationen kann aus dem Tiefpass ein Hochpass oder auch eine Bandpass gebildet werden.

Tiefpass 1. Ordnung

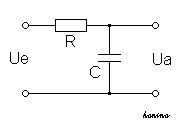
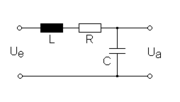
Im einfachsten Fall besteht ein Tiefpass aus einer Widerstand-Kondensator-Kombination (RC-Glied). Ein solcher passiver Tiefpass 1. Ordnung sieht folgendermaßen aus:

Amplitudenverlauf Tiefpass 1. Ordnung

Spannung V_C an der Kapazität als Funktion der Zeit

Von der Eingangsspannung 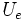$U_e\$ erscheint am Ausgang gemäß der Spannungsteilerformel nur der Anteil $U_a\$:

$U_a = U_e \cdot \frac{\vert X_C \vert}{\sqrt{X_C^2 + R^2}} = U_e \cdot \frac {1} {\sqrt{ 1 + (\omega CR)^2}}$

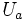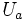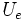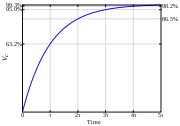
wobei $U_a\$ und $U_e\$ die Beträge der Aus- bzw. Eingangsspannung bezeichnen.

Unter der Grenzfrequenz f_c (cutoff frequency) versteht man diejenige Frequenz, bei der $U_{a} = U_{e}/\sqrt{2}\approx U_{e} \cdot 0{,}707$
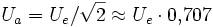
(d. h. U_a gegenüber U_e um etwa 3 Dezibel abgeschwächt) ist. Die Grenzfrequenz berechnet sich zu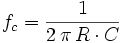 $f_c=\frac{1}{2\,\pi\,R\cdot C}$

Da X_C, der Blindwiderstand des Kondensators mit steigender Frequenz kleiner wird,

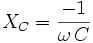$X_C = \frac{-1}{\omega\,C}$ mit $\omega = 2\,\pi\,f$,

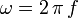geht das Teilungsverhältnis mit sinkender Frequenz gegen 1, für Gleichspannung (Frequenz f = 0) wird $U_a = U_e\$.

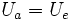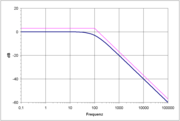
In logarithmischer Darstellung nimmt die Dämpfung oberhalb der Grenzfrequenz um 6 dB/Oktave bzw. 20 dB/Dekade zu.

Aktiver Tiefpass

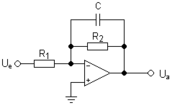
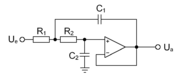
Mit Operationsverstärkern können aktive Tiefpässe realisiert werden. Diese haben den Vorteil, dass der Frequenzgang unabhängig von der am Ausgang angeschlossenen Last ist. Der Betrag der Ausgangsspannung dieses Tiefpasses ist

$U_a = -U_e \cdot \frac {R_2} {R_1} \cdot \frac{\vert X_C \vert}{\sqrt{X_C^2 + R_2^2}}\$.

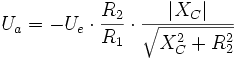Die Grenzfrequenz ist hier die Frequenz, bei der die Verstärkung auf das 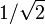$1/\sqrt{2}$-fache der Gleichspannungsverstärkung (R₂ / R₁) abgefallen ist.

Herleitung der Formel

laut Spannungsteiler gilt:

$\frac {\underline {u_a}(t)}{\underline {u_e}(t)} = \frac{\underline {Z_c}}{\underline {Z_c} + R} \ = \frac{\frac{1}{{\mathrm j}{\omega}{C}}}{\frac{1}{{\mathrm j}{\omega}{C}} + R}= \frac{1}{1 + {\mathrm j}{\omega}{C}{R}} \qquad \text{mit} \qquad j^2=-1$

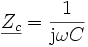mit $\underline {Z_c} = \frac{1}{{\mathrm j}{\omega}{C}}$ = Widerstandsoperator bzw. Impedanz des Kondensators

komplexe Umformung

$z = x + \mathrm j y = 1 + {\mathrm j}{\omega}{C}{R} \,$

$z = r \mathrm e^{{\mathrm j}{\varphi}} \Rightarrow r = \sqrt{x^2 + y^2} \Rightarrow {\varphi} = \arctan\left(\frac yx\right)$

$z = \sqrt{1 + ({\omega}{C}{R})^2} \cdot {\mathrm e^{{\mathrm j} \cdot {\arctan({\omega}{C}{R})}}}$

$\frac {\underline {u_a}(t)}{\underline {u_e}(t)} = \frac {1} {\sqrt{ 1 + (\omega CR)^2}} \cdot {\mathrm e^{-{\mathrm j} \cdot {\arctan({\omega}{C}{R})}}}$

diese Gleichung stellt die normierte Spannungsortskurve dar (Bildbereich)

Rücktransformation

(nach den Transformationsregeln für harmonische Schwingungen)

$a = {\hat a} \sin({\omega}t + {\varphi}) \Leftrightarrow \underline {a} = {\hat a} \cdot {e^{{\mathrm j} \cdot ({{\omega}{t} + {\varphi}})}}$

$\frac {u_a(t)}{u_e(t)} = \frac {1} {\sqrt{ 1 + (\omega CR)^2}} \cdot \sin(- \arctan({ \omega}{C}{R}))$

Gleichungen

Amplitudengang

$H(\omega) = \frac {\hat u_a}{\hat u_e} = \frac {1} {\sqrt{ 1 + (\omega CR)^2}}$

Phasengang

${\varphi}(\omega) = {-\arctan({\omega}{C}{R})}$

Gleichung zur Darstellung im Bode-Diagramm

(Amplitudenverlauf Tiefpass 1. Ordnung)

$H_\mathrm{dB}(\omega) = 20 \lg \frac {1} {\sqrt{ 1 + (\omega CR)^2}}$

Umformung zur hier verwendeten Formel

(mit Blindwiderstand)

$\frac {1} {\sqrt{ 1 + (\omega CR)^2}}=\frac {1} {\sqrt{({\omega C})^2 ((\frac {1}{\omega C})^2 + R^2)}}=\frac {(\frac {1}{\omega C})} {\sqrt{ ((\frac {1}{\omega C})^2 + R^2)}}=\frac{\vert X_C \vert}{\sqrt{X_C^2 + R^2}}$

Tiefpass 2. Ordnung

Einen Tiefpass zweiter Ordnung erhält man, indem man R durch eine Reihenschaltung von R mit einer Induktivität L ersetzt, da diese ihrerseits eine – und zwar zum Kondensator gegenläufige – Frequenzabhängigkeit besitzt. Dabei wird R so groß gewählt, dass keine oder nur eine geringe Resonanzüberhöhung des Frequenzgangs entsteht.

Passiver Tiefpass 2. Ordnung

Aktiver Tiefpass 2. Ordnung

Die Übertragungsfunktion eines solchen Tiefpasses ist

$H(\omega)=\frac{\mathrm j\, X_C}{R+\mathrm j(X_L+X_C)}$

mit $X_L=\omega \, L, \quad X_C=\frac{-1}{\omega \, C}\, , \quad \omega = 2\,\pi\,f$.

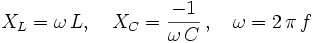Der Betrag der Übertragungsfunktion ist

$\begin{align} \frac{U_a}{U_e} &= \vert H(\omega) \vert = \frac{\vert X_C \vert}{\sqrt{R^2+(X_L+X_C)^2}}\\ &=\sqrt{\frac{1}{\omega^4 \, L^2 \, C^2 + \omega^2 \, R^2 \, C^2 - 2 \, \omega^2 \, L \, C + 1 }} \end{align}$

Damit fällt die Ausgangsspannung U_a oberhalb von f_G schneller (mit 12 dB/Oktave bzw. 40 dB/Dekade) ab, da nun nicht nur |X_C| kleiner sondern zugleich |X_L| größer wird.

In dieser Variante werden im Niederfrequenzbereich große Induktivitäten gebraucht (bis zu mehreren Henry). Diese haben schlechte elektrische Eigenschaften und besitzen recht große Dimensionen. Deshalb werden Tiefpässe zweiter und höherer Ordnung heutzutage üblicherweise durch Operationsverstärker-Schaltungen realisiert. Diese Filter werden als aktive Tiefpässe (bzw. aktive Filter) bezeichnet und sind nach ihren Erfindern auch als Sallen-Key-Filter bekannt.

Im Hochfrequenzbereich, beispielsweise beim Bau von Sendeanlagen ist R immer Null, um Wärmeverluste zu vermeiden. Diese Schaltung wird aus zwei Gründen verwendet:

• Sie dämpft Oberwellen, die durch den C-Betrieb der Elektronenröhren entstehen, auf ein zulässiges Maß.
• Die Werte der Bauelemente können so gewählt werden, dass die Schaltung als Resonanztransformator wirkt und eine Leistungsanpassung zwischen Sender und Antenne erlaubt.

Tiefpass n-ter Ordnung

Durch das Hintereinanderschalten von mehreren Tiefpässen kann man dessen Ordnung erhöhen, beispielsweise bilden zwei hintereinandergeschaltete Tiefpässe 2. Ordnung einen Tiefpass 4. Ordnung. Die Dämpfung ändert sich hierbei oberhalb der Grenzfrequenz mit 4•20 dB/Dekade = 80 dB/Dekade, was einer Flankensteilheit von 24 dB/Oktave entspricht.

Zwei zusammengeschaltete Tiefpässe mit gleicher Grenzfrequenz ergeben aber keinen Tiefpass höherer Ordnung derselben Grenzfrequenz. Für die Dimensionierung eines Tiefpasses mit gewünschter Grenzfrequenz stehen spezielle Formeln und Tabellen zur Verfügung.

Zusätzlich tritt das Problem auf, dass ein Tiefpass in einer Kette vom Ausgangswiderstand des vorgeschaltenen und dem Eingangswiderstand des nachgeschalteten Tiefpasses beeinflusst wird. Diesem Effekt kann mit Impedanzwandlern entgegengewirkt werden.

Allgemein werden für ein Filter n-ter Ordnung n speichernde Elemente (also Kondensatoren oder Spulen) benötigt.

Die Dämpfung eines Tiefpasses n-ter Ordnung nimmt oberhalb der Grenzfrequenz mit n·20 dB/Dekade zu.

Emphasis und Deemphasis

Bei der statischen Frequenzgangveränderung, der Emphasis und der Deemphasis wird anstatt der Grenzfrequenz üblicherweise die Zeitkonstante angegeben [1].

Literatur

• Ulrich Tietze, Christoph Schenk und Eberhard Gamm: Halbleiter-Schaltungstechnik. Springer-Verlag, 2002, 12. Auflage, ISBN 3-540-42849-6

Siehe auch

• Akustische Oberflächenwellen-Filter
• Blindwiderstand von Kondensator und Spule
• PT1-Glied
• Resonanztransformator

Weblinks

• RC und RL-Schaltungen, Berechnung des Amplitudengangs und Phasengangs - pdf
• Rechenschritte mit komplexen Übertragungsfunktionen
• R-C Filter und Grenzfrequenz - Tiefpass und Hochpass