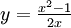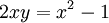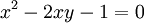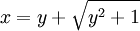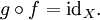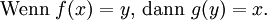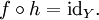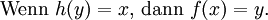Umkehrfunktionen

Die Umkehrfunktion oder inverse Funktion einer bijektiven Funktion ist die Funktion, die jedem Element der Zielmenge sein eindeutig bestimmtes Urbildelement zuweist. (Bei bijektiven Funktionen hat die Urbildmenge jedes Elements genau ein Element.) Eine Funktion, deren Umkehrfunktion existiert, wird auch als invertierbar bezeichnet.

Schreibweise

Wenn 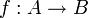$f : A \rightarrow B$ eine bijektive Funktion ist, dann bezeichnet 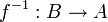$f^{-1} : B \rightarrow A$ die Umkehrfunktion. Dabei ist das ⁻¹ nicht mit einer negativen Potenz bezüglich der Multiplikation zu verwechseln; es handelt sich vielmehr um die Umkehrung bezüglich der Hintereinanderausführung (Verkettung) von Funktionen.

Der Funktionswert f ⁻¹(y) ist definiert als das (eindeutig bestimmte) x in A, das die Gleichung f(x) = y erfüllt.

Beispiele

• Sei 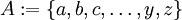$A := \{ a, b, c, \ldots , y, z \}$ die Menge der 26 Buchstaben des lateinischen Alphabets und sei 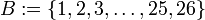$B := \{ 1, 2, 3, \ldots , 25, 26 \}$. Die Funktion 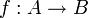$f : A \rightarrow B$, die jedem Buchstaben die entsprechende Nummer im Alphabet zuordnet, ist bijektiv und 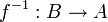$f^{-1} : B \rightarrow A$ ist gegeben durch f ^{− 1}(n) = „der n-te Buchstabe im Alphabet“.

• Sei 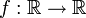$f: \mathbb{R} \rightarrow \mathbb{R}$ die Funktion mit f(x) = 3x + 2. Diese ist bijektiv und die Umkehrfunktion ist gegeben durch
  f ^{− 1}(y) = (y − 2) / 3.

• Sei 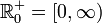$\mathbb{R}_0^+ = [ 0, \infty )$ die Menge der nichtnegativen reellen Zahlen und 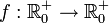$f : \mathbb{R}_0^+ \rightarrow \mathbb{R}_0^+$ mit f(x) = x² eine eingeschränkte Quadratfunktion. Dann ist f bijektiv und die Umkehrfunktion 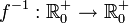$f^{-1} : \mathbb{R}_{0}^{+} \rightarrow \mathbb{R}_{0}^{+}$ ist gegeben durch
  $f^{-1}(x) = \sqrt{x}$.

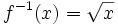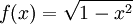• Für $f:\ [0, 1] \to [0, 1]$ mit $f(x) = \sqrt{1-x^2}$ gilt f ^{− 1} = f.

• Die Umkehrfunktion der Exponentialfunktion ist die Logarithmusfunktion.

• Die Umkehrfunktionen von Einschränkungen der trigonometrischen Funktionen Sinus (sin), Kosinus (cos) und Tangens (tan) auf geeignete Definitions- und Zielbereiche (auf denen diese Einschränkungen bijektiv sind) heißen Arkusfunktionen: Arkussinus (arcsin), Arkuskosinus (arccos) und Arkustangens (arctan).

• Die Umkehrungen geeigneter Einschränkungen der Hyperbelfunktionen Sinus Hyperbolicus (sinh), Cosinus Hyperbolicus (cosh) und Tangens Hyperbolicus (tanh) heißen Areafunktionen: Areasinus Hyperbolicus (arsinh), Areacosinus Hyperbolicus (arcosh) und Areatangens Hyperbolicus (artanh).

Eigenschaften

• Die Umkehrfunktion der Umkehrfunktion ist die ursprüngliche Funktion, d.h.
  (f ^{− 1}) ^{− 1} = f.

• Ist 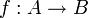$f : A \rightarrow B$ eine Bijektion, dann gilt für die Umkehrfunktion:
    f(f ^{− 1}(x)) = x für alle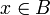 $x \in B$,
    f ^{− 1}(f(x)) = x für alle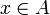 $x \in A$.
  Mit Hilfe der Verkettung von Funktionen lässt sich dies auch so schreiben:
    $f \circ f^{-1} = \operatorname{id}_B$
    $f^{-1} \circ f = \operatorname{id}_A$.

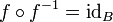
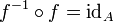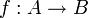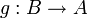• Sind $f : A \rightarrow B$ und $g : B \rightarrow A$ zwei Funktionen mit den Eigenschaften
    f(g(x)) = x für alle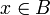 $x \in B$,
    g(f(x)) = x für alle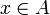 $x \in A$,
  dann sind beide Funktionen bijektiv und g ist die Umkehrfunktion von f.

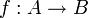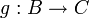• Sind die Funktionen $f : A \rightarrow B$ und $g : B \rightarrow C$ bijektiv, dann gilt dies auch für die Verkettung 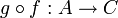$g \circ f : A \rightarrow C$. Die Umkehrfunktion von 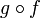$g \circ f$ ist dann $f^{-1} \circ g^{-1}$.

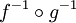• Eine Funktion 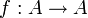$f : A \rightarrow A$ kann ihre eigene Umkehrfunktion sein. Es gilt dann 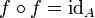$f \circ f = \operatorname{id}_A$ und man nennt f eine Involution.

• Ist 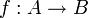$f : A \rightarrow B$ eine Bijektion, wobei A und B Teilmengen von $\mathbb{R}$ sind, dann entsteht der Graph der Umkehrfunktion, indem man den Graph von f an der Diagonalen y = x spiegelt.

• Ist 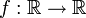$f : \mathbb{R} \rightarrow \mathbb{R}$ differenzierbar, 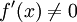$f'(x) \neq 0$ und y: = f(x), dann gilt die folgende Umkehrregel:
  $(f^{-1})'(y)=\frac{1}{f'(f^{-1}(y))}$.

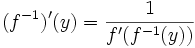Berechnung der Umkehrfunktion

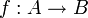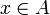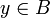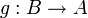Ist $f : A \to B$ eine Funktion und gelingt es, die Gleichung y = f(x) durch Äquivalenzumformung in die Form x = g(y) zu bringen, also äquivalent nach x aufzulösen (wobei $x \in A$, $y \in B$ und $g: B \to A$ gilt), dann ist f als bijektiv nachgewiesen und die Umkehrfunktion von f (nämlich g) bestimmt.

Beispiele:

• Sei 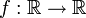$f: \mathbb{R} \to \mathbb{R}$ mit f(x) = 2x − 1. Die folgenden Gleichungen sind äquivalent:

  y = 2x − 1

  2x = y + 1

  $x = \tfrac{y+1}{2}$

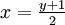
Die Umkehrfunktion von f lautet daher 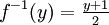$f^{-1}(y)=\tfrac{y+1}{2}$. Da es üblich ist, das Argument mit x zu bezeichnen, schreibt man auch: $f^{-1}(x)=\tfrac{x+1}{2}$.

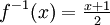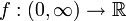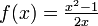• Sei $f: (0, \infty) \to \mathbb{R}$ mit $f(x) = \tfrac{x^2-1}{2x}$. Die folgenden Gleichungen sind äquivalent (man beachte, dass x > 0 gilt):

  $y = \tfrac{x^2-1}{2x}$

  $2xy = x^2 - 1\$

  $x^2 - 2xy - 1 = 0\$

  $x = y + \sqrt{y^2+1}$

(Die zweite Lösung der quadratischen Gleichung entfällt, da x als positiv vorausgesetzt ist.) Die Umkehrfunktion lautet also: $f^{-1}(y) = y + \sqrt{y^2+1}$

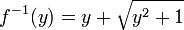
Verallgemeinerungen

Für allgemeinere Anwendungen ist der oben eingeführte Begriff der Umkehrfunktion als Inverses einer Bijektion zu eng. Entsprechend existieren Verallgemeinerungen für solche Gegebenheiten, von denen zwei nachfolgend vorgestellt werden.

Links- und Rechts-Inverse

Für eine Funktion 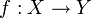$f: X \rightarrow Y$ heißt eine Funktion 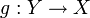$g: Y \rightarrow X$ links-invers (oder Retraktion), wenn

$g \circ f = \mathrm{id}_X . \,\!$

Das heißt, die Funktion g erfüllt

$\text{Wenn }f(x) = y\text{, dann }g(y) = x . \,\!$

g muss also der gleich der Umkehrfunktion der von f im Wertebereich von f sein, kann aber beliebige Werte für Elemente aus Y annehmen, die nicht Resultat von f sind. Eine Funktion f hat Links-Inverse genau dann, wenn sie injektiv (linkseindeutig) ist.

Eine Rechts-Inverse von f (oder, bei Faserbündeln, ein Schnitt von f) ist eine Funktion 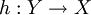$h: Y \rightarrow X$, so dass

$f \circ h = \mathrm{id}_Y . \,\!$

Das heißt, die Funktion h erfüllt

$\text{Wenn }h(y) = x\text{, dann }f(x) = y . \,\!$

h(y) kann also jedes Element von X sein, das von f auf y abgebildet wird. Eine Funktion f hat Rechts-Inverse genau dann, wenn sie surjektiv (rechtstotal) ist. (Die Konstruktion solch einer Inversen erfordert im allgemeinen das Auswahlaxiom.)

Eine Funktion kann mehrere Links- oder Rechts-Inverse haben. Sie hat aber genau eines, wenn sie sowohl ein Links- als auch ein Rechts-Inverse hat, die dann gleich sind.

Beispiele

Links-Inverse treten oft als Inverse von Einbettungen auf.

Zum Beispiel sei f eine Funktion, die jedem Farbnamen ('rot', 'grün', 'blau', usw.) seine Farbe zuweist. Dann wäre ein Retrakt eine Funktion g, die für jede Farbe einen Farbnamen ergibt.

Als numerisches Beispiel sei f die Einbettung von $\mathbb{Z}$ in $\mathbb{Q}$. g kann dann z.B. die größte ganze Zahl liefern, die kleiner oder gleich dem Argument ist.

Rechts-Inverse treten oft als Funktionen auf, die Repräsentanten einer Menge bestimmen.

Sei beispielsweise 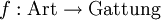$f: \text{Art} \rightarrow \text{Gattung}$ eine Funktion, die jeder Art ihre Gattung zuweist. Das Rechts-Inverse h ist eine Funktion, die für jede Gattung eine typische Art benennt. Politische Vertretung liefert viele Beispiele. Hier könnte f etwa die Staatsangehörigkeit eines Menschen sein, h das Staatsoberhaupt eines Staates.

Als mathematisches Beispiel für ein Rechts-Inverses wäre f eine Auswertungsfunktion, die Termen einen Wert zuweist (diese ausrechnet). So haben etwa die Terme '2/4', '3/6', '1-1/2' usw. alle denselben Wert 0,5. h wäre dann eine Funktion, die für jeden Wert einen typische Term liefert, hier vielleicht '1/2'.