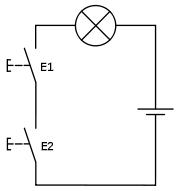
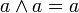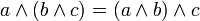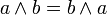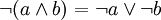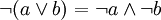Und-Verknüpfung

Technische Realisierung: Wenn die Taster E1 und E2 gleichzeitig betätigt werden, leuchtet die Lampe.

Als Konjunktion wird in der Logik eine bestimmte Verknüpfung zweier Aussagen oder Aussagefunktionen bezeichnet. Gelesen wird die Konjunktion zweier Aussagen a sowie b meist als „a und b“. In der klassischen Logik ist die Konjunktion zweier Aussagen genau dann wahr, wenn beide verknüpfte Aussagen wahr sind.

Gemeint sein kann mit dem Wort Konjunktion die verknüpfte Aussage als Ganzes (der Satz „a und b“), das Verknüpfungszeichen (Junktor) beziehungsweise -wort „und“, aber auch – im Fall einer wahrheitsfunktionalen Konjunktion – die Wahrheitsfunktion, mit der sich der Wahrheitswert der verknüpften Aussage „a und b“ aus den Wahrheitswerten ihrer Teilsätze (a, b) bestimmen lässt.

Die Konjunktion in der klassischen, zweiwertigen Logik

In der klassischen Logik ist die Konjunktion zweier Aussagen a und b genau dann wahr, wenn sowohl a als auch b wahr sind. Veranschaulicht wird das durch folgende Wahrheitstabelle:

a	b	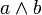$a \land b$
wahr	wahr	wahr
wahr	falsch	falsch
falsch	wahr	falsch
falsch	falsch	falsch

Gebräuchliche Schreibweisen für die Konjunktion sind 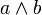${a \land b}$, „a & b“, „a ▪ b“, „a ∩ b“ (Peano) und „ab“. In der polnischen Notation wird die Konjunktion als „Kab“ geschrieben.

Eine Konjunktion selbst ist ein Boolescher Ausdruck. In der Digitaltechnik werden konjunktiv verknüpfte Variablen auch Produktterm genannt.

Für die Konjunktion gelten unter anderem folgende wichtige Gesetze:

• Idempotenz: $a\land a=a$
• Assoziativgesetz: $a\land(b\land c) = (a\land b)\land c$
• Kommutativgesetz: $a\land b=b\land a$
• De Morgansche Regeln:

$\neg {(a \land b)} = \neg{a} \lor \neg{b}$

$\neg {(a \lor b)} = \neg{a} \land \neg{b}$

In Kalkülen des natürlichen Schließens werden als Schlussregeln für die Konjunktion die Konjunktionseinführung und die Konjunktionsbeseitigung verwendet. Mit der Konjunktionseinführung lässt sich aus zwei Aussagen a, b auf deren Konjunktion 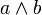${a \land b}$ schließen; mit der Konjunktionsbeseitigung lässt sich aus der Konjunktion 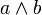${a \land b}$ auf jedes der Konjunkte a beziehungsweise b schließen.

Die Konjunktion in mehrwertigen Logiken

Beim Aufstellen einer mehrwertigen Konjunktion bemüht man sich im allgemeinen, möglichst viele Eigenschaften der klassischen Konjunktion beizubehalten, insbesondere die Assoziativität und Kommutativität. Damit kann eine mehrwertige Konjunktion axiomatisch folgendermaßen definiert werden:

T(a,b) ist eine Konjunktion wenn gilt:

• Kommutativität: T(a,b) = T(b,a)
• Assoziativität: T(a,(T(b,c)) = T(T(a,b),c)
• Monotonie: $a > b \Rightarrow T(a,c) \ge T(b,c)$
• Einselement: T(1,a) = a

Weitere sinnvolle, aber nicht notwendige Eigenschaften sind Stetigkeit und Idempotenz.

In dreiwertigen Logiken wurden beispielsweise folgende Konjunktionen aufgestellt:

Konjunktion in der dreiwertigen Logik Ł3 von Jan Łukasiewicz (1920)

A	B	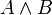$A \land B$
1	1	1
1	0,5	0,5
1	0	0
0,5	1	0,5
0,5	0,5	0,5
0,5	0	0
0	1	0
0	0,5	0
0	0	0

Konjunktion in der dreiwertigen Logik B3 von Dimitri Analtoljewitsch Bočvar (1938)

A	B	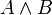$A \land B$
1	1	1
1	0,5	0,5
1	0	0
0,5	1	0,5
0,5	0,5	0,5
0,5	0	0,5
0	1	0
0	0,5	0,5
0	0	0

Die Konjunktion und das Wort „und“

Das natürlichsprachliche Wort „und“ ist nicht mit der Konjunktion im Sinn der Logik identisch: Einerseits wird das Wort „und“ nicht immer im Sinn der logischen Konjunktion verwendet, andererseits kann die Konjunktion auch durch andere sprachliche Mittel ausgedrückt werden.

Neben der logischen Konjunktion wird das natürlichsprachliche Wort „und“ zum Beispiel verwendet, um ein zeitliches Nacheinander („und dann“, Beispiel: „Ich aß und ging (dann) nach Hause.“) und sogar eine kausale Beziehung („und deshalb“, Beispiel: „Der Patient nahm das Medikament und wurde (deshalb) gesund“) auszudrücken.

Siehe auch

• Und-Gatter
• Aussagenlogik
  • Junktor
    • Äquivalenz (XNOR-Gatter)
    • Subjunktion (Implikation)
    • Negation (Komplement-Gatter)
    • Kontravalenz (XOR-Gatter)
    • Disjunktion (Oder-Gatter)