- Uniformisierende
-
Im mathematischen Teilgebiet der Algebra sind diskrete Bewertungsringe gewisse lokale Ringe mit besonders guten Eigenschaften.
Definition: Ein diskreter Bewertungsring ist ein lokaler Hauptidealring, der kein Körper ist. Ein Erzeuger des maximalen Ideals heißt uniformisierendes Element oder kurz eine Uniformisierende. Man schreibt auch kurz DVR (für discrete valuation ring) oder DBR.
Eigenschaften
- Ein diskreter Bewertungsring ist ein Dedekindring, insbesondere ein regulärer lokaler Integritätsring.
- Das Spektrum SpecR eines diskreten Bewertungsringes R besteht aus genau zwei Punkten:
Einem abgeschlossenen Punkt, dem speziellen Punkt, zugehörig zum maximalen Ideal (π) (wenn π das uniformisierende Element ist) und einem nicht abgeschlossenen (aber offenen) Punkt, dem generischen Punkt (0).
- Für einen diskreten Bewertungsring R wird durch
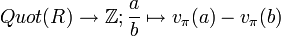 eine diskrete Bewertung auf dem Quotientenkörper definiert (wenn vπ(a) = n für (a) = (π)n in R). Diese Bewertung hat R als Bewertungsring.
eine diskrete Bewertung auf dem Quotientenkörper definiert (wenn vπ(a) = n für (a) = (π)n in R). Diese Bewertung hat R als Bewertungsring. - Ordnet man einem diskret bewerteten Körper F seinen Bewertungsring
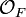 zu und wendet darauf obige Konstruktion an, so erhält man einen diskret bewerteten Körper, der isomorph zu F ist. Mit anderen Worten: Diese Konstruktionen induzieren eine Äquivalenz von Kategorien zwischen diskret bewerteten Körpern und diskreten Bewertungsringen.
zu und wendet darauf obige Konstruktion an, so erhält man einen diskret bewerteten Körper, der isomorph zu F ist. Mit anderen Worten: Diese Konstruktionen induzieren eine Äquivalenz von Kategorien zwischen diskret bewerteten Körpern und diskreten Bewertungsringen.
Beispiele
- Der Ring der ganzen p-adischen Zahlen
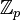 für jede Primzahl p.
für jede Primzahl p. - Der Ring der rationalen Zahlen, die p-adisch ganz sind, für eine Primzahl p:
- Der Ring der formalen Potenzreihen k[[T]] in einer Unbestimmten über einem Körper k.
- Der Ring der konvergenten Potenzreihen
- Der lokale Ring zu einem glatten Punkt einer algebraischen Kurve.
Wikimedia Foundation.

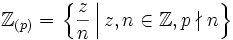
![\mathbb C\{T\}=\left.\left\{\sum_{i=0}^\infty a_iT^i\,\right|\exists r>0\colon \sum_{i=0}^\infty a_iz^i\ \mathrm{konvergiert\ f\ddot ur}\ |z|<r\right\}\subset\mathbb C[[T]].](/pictures/dewiki/52/463fdb71279b974658e99752d4223203.png)