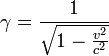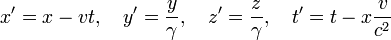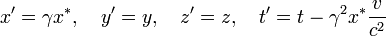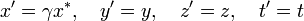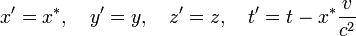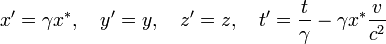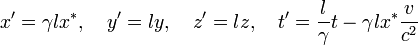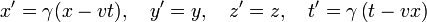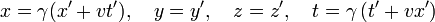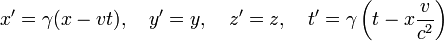Voigt-Transformation

Die Lorentz-Transformation verknüpft wie die Galilei-Transformation die Koordinaten x,y,z,t eines Ereignisses in einem bestimmten Inertialsystem, mit den Koordinaten x',y',z',t' des gleichen Ereignisses in einem anderen Inertialsystem, welches in positiver x-Richtung mit der Geschwindigkeit v relativ zum ersten System bewegt ist. Jedoch im Gegensatz zur Galilei-Transformation beinhaltet sie neben dem Relativitätsprinzip die Konstanz der Lichtgeschwindigkeit in allen Inertialsystemen, und bildet somit die mathematische Grundlage für die spezielle Relativitätstheorie.

Erste Näherungen an diese Transformation wurden von Woldemar Voigt (1887) und Hendrik Lorentz (1895) veröffentlicht. wobei bei diesen Autoren das ungestrichene System als im Äther ruhend betrachtet wurde, und das „bewegte“ gestrichene System wurde mit der Erde identifiziert. Diese Transformation wurden von Joseph Larmor (1897, 1900) und Lorentz (1899, 1904) vervollständigt und durch Henri Poincaré (1905), welcher der Transformation ihren Namen gab, in ihre moderne Gestalt gebracht. Albert Einstein (1905) schließlich konnte die Gleichungen aus wenigen Grundannahmen ableiten, und zeigte den Zusammenhang der Transformation mit fundamentalen Änderungen der Begriffe von Raum und Zeit auf.

In diesem Artikel werden die historischen Ausdrücke durch moderne ersetzt, wobei

$\gamma =\frac1{\sqrt{1- \frac{v^2} {c^2}}}$

der Lorentz-Faktor ist, v ist die Relativgeschwindigkeit zwischen den Körpern, und c ist die Lichtgeschwindigkeit.

Voigt (1887)

Im Zusammenhang mit dem Dopplereffekt und einem inkompressiblen Medium bzw. Äther entwickelte Voigt (1887) die Voigt-Transformation, welche die Wellengleichung unverändert ließen und in moderner Notation die Form hatte:^[1][2]

$x^{\prime}=x-vt,\quad y^{\prime}=\frac{y}{\gamma},\quad z^{\prime}=\frac{z}{\gamma},\quad t^{\prime}=t-x\frac{v}{c^{2}}$

Wenn die rechten Seiten dieser Gleichungen mit γ multipliziert werden, ergeben sich die Lorentz-Transformationen. Jedoch ist die Voigt-Transformation nicht symmetrisch und verletzt das Relativitätsprinzip. Lorentz (1909) erklärte später, dass wenn er Kenntnis von diesen Gleichungen besessen hätte, er sie in seiner Elektronentheorie hätte verwenden können. Auch Hermann Minkowski sagte 1908 während einer Diskussion zu Bucherers Experimenten, an der auch Voigt beteiligt war:

„Minkowski: Historisch will ich noch hinzufügen, daß die Transformationen, die bei dem Relativitätsprinzip die Hauptrolle spielen, zuerst mathematisch von Voigt im Jahre 1887 behandelt sind. Voigt hat damals bereits mit ihrer Hilfe Folgerungen in bezug auf das Dopplersche Prinzip gezogen.
Voigt: Herr Minkowski erinnert an eine alte Arbeit von mir. Es handelt sich dabei um Anwendungen des Dopplerschen Prinzips, die in speziellen Teilen auftreten, aber nicht auf Grund der elektromagnetischen, sondern auf Grund der elastischen Theorie des Lichtes. Indessen haben sich damals bereits einige derselben Folgerungen ergeben, die später aus der elektromagnetischen Theorie gewonnen sind.“

Lorentz (1892, 1895)

Lorentz entwickelte 1892 ein Modell, in dem der Äther vollständig in Ruhe ist, wodurch im Äther die Lichtgeschwindigkeit in alle Richtungen denselben Wert hat. Um nun die Optik bewegter Körper berechnen zu können, führte Lorentz folgende Hilfsvariablen zur Transformation vom Äthersystem in ein relativ dazu bewegtes System ein:^[3]

$x^{\prime}=\gamma x^{*},\quad y^{\prime}=y,\quad z^{\prime}=z,\quad t^{\prime}=t-\gamma^{2} x^{*}\frac{v}{c^{2}}$

wo x^* die Galilei-Transformation x-vt ist. Während nun t die „wahre“ Zeit für im Äther ruhende Systeme, ist die Zeit t' eine mathematische Hilfsvariable, welche für Berechnungen von im Äther bewegten Systemen benutzt wird. Eine solche „Ortszeit“ wurde bereits von Voigt benutzt, jedoch gab Lorentz später an, zu diesem Zeitpunkt keine Kenntnis von dessen Arbeit besessen zu haben. Wichtig dabei ist auch, dass Lorentz und später auch Larmor die Transformationen immer in 2 Schritten formulierten. Zuerst die Galilei-Transformation, und danach davon getrennt erst die Erweiterung zum „fiktiven“ elektromagnetischen System mit Hilfe der Lorentz-Transformation. Ihre symmetrische Gestalt erhielten die Gleichungen erst durch Poincaré.

1895 entwickelte er die Lorentzsche Elektrodynamik sehr viel systematischer weiter, wobei ein fundamentales Konzept das "Theorem der korrespondierenden Zustände" für Größen zu v/c war. Aus ihm folgt, dass ein im Äther bewegter Beobachter annähernd dieselben Beobachtungen in seinem „fiktiven“ (elektromagnetischen) Feld macht wie ein im Äther ruhender Beobachter in seinem „realen“ Feld. Das heißt solange die Geschwindigkeiten relativ zum Äther vergleichsweise gering sind, haben die maxwellschen Gleichungen für alle Beobachter dieselbe Form. Für die Elektrostatik bewegter Körper benutzte er die Transformationen, welche die Dimensionen der Körper folgendermaßen änderte:^[4]

$x^{\prime}=\gamma x^{*},\quad y^{\prime}=y,\quad z^{\prime}=z,\quad t^{\prime}=t$

Als eine zusätzliche und unabhängige Hypothese behauptete Lorentz (1892b, 1895) (ohne Beweis wie er zugab), dass auch die intermolekularen Kräfte und somit auch materielle Körper auf eine ähnliche Weise deformiert werden, und führte (1892b) zur Erklärung des Michelson-Morley-Experiments die Längenkontraktion ein. Aber während für Lorentz die Längenkontraktion ein realer, physikalischer Effekt war, bedeutete für ihn die Ortszeit vorerst nur eine Vereinbarung oder nützliche Berechnungsmethode. Hingegen für die Optik bewegter Körper benutzte er die Transformationen:

$x^{\prime}=x^{*},\quad y^{\prime}=y,\quad z^{\prime}=z,\quad t^{\prime}=t-x^{*}\frac{v}{c^{2}}$

Mit Hilfe der Ortszeit konnte Lorentz die Aberration des Lichts, den Dopplereffekt und die beim Fizeau-Experiment gemessene Abhängigkeit der Lichtgeschwindigkeit in bewegten Flüssigkeiten erklären.

Larmor (1897, 1900)

Larmor wusste zu dieser Zeit, dass das Michelson–Morley-Experiment genau genug war, um bewegungsbedingte Effekte von der Größe 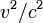$v^2/c^2 \,$ aufzuzeigen, und so suchte er eine Transformation, welche auch für diese Größen gültig ist. Obwohl er dabei einem sehr ähnliche Schema wie Lorentz folgte, ging er über dessen Arbeit von 1895 hinaus und modifizierte die Gleichungen, sodass er 1897 und etwas übersichtlicher 1900 als erster die komplette Lorentz-Transformation aufstellen konnte:^[5][6]

$x^{\prime}=\gamma x^{*},\quad y^{\prime}=y,\quad z^{\prime}=z,\quad t^{\prime}=\frac{t}{\gamma}-\gamma x^{*}\frac{v}{c^{2}}$

Er zeigte, dass die Maxwell-Gleichungen invariant unter dieser 2-Schritte-Transformation waren (allerdings führte er den Beweis nur für Größen zweiter Ordnung durch, nicht für alle Ordnungen). Larmor bemerkte überdies, dass wenn eine elektrische Konstitution der Moleküle angenommen wird, die Längenkontraktion eine Konsequenz der Transformation sind. Er war auch der Erste, der eine Art Zeitdilatation als Konsequenz der Gleichungen bemerkte, denn periodische Vorgänge von bewegten Objekten laufen im Verhältnis 1 / γ langsamer als bei ruhenden Objekten ab.

Lorentz (1899, 1904)

Auch Lorentz leitete 1899 durch die Erweiterung des Theorems der korrespondierenden Zustände die vollständige Transformation ab. Jedoch benutzte er den unbestimmten Faktor ε als Funktion von v. Wie Larmor bemerkte Lorentz eine Art Zeitdilatation, da er erkannte, dass die Vibrationen eines oszillierenden Elektrons, welches sich relativ zum Äther bewegen, langsamer verlaufen. Der unbestimmte Faktor ε bzw. 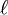$\ell$ wurde dann 1904 von Lorentz gleich 1 gesetzt und so erreichte er dieselbe Form wie Larmor:^[7]

$x^{\prime}=\gamma lx^{*},\quad y^{\prime}=ly,\quad z^{\prime}=lz,\quad t^{\prime}=\frac{l}{\gamma}t-\gamma lx^{*}\frac{v}{c^{2}}$

In diesem Zusammenhang leitete er bereits 1899 die korrekten Formeln für die Geschwindigkeitsabhängigkeit der Masse ab und er schloss 1904, dass diese Transformation auf alle Kräfte der Natur angewendet werden müsse, nicht nur auf elektrische, und deshalb ist die Längenkontraktion eine Konsequenz der Transformation. Inwieweit Larmor (1897) von Lorentz (1895) und umgekehrt Lorentz (1904) von Larmor (1900) beeinflusst wurde, ist nicht bekannt.

Poincaré (1900, 1905)

Weder Lorentz noch Larmor gaben eine klare Interpretation des Ursprungs der Ortszeit an. 1900 interpretierte Poincaré jedoch die Ortszeit als Ergebnis einer mit Lichtsignalen durchgeführten Synchronisation. Er nahm an, dass zwei im Äther bewegte Beobachter A und B ihre Uhren mit optischen Signalen synchronisieren. Da sie glauben sich in Ruhe zu befinden, gehen sie von einer konstanten Lichtgeschwindigkeit in alle Richtungen aus, sodass sie jetzt nur noch die Lichtlaufzeiten berücksichtigen und ihre Signale kreuzen müssen, um die Synchronität der Uhren zu überprüfen. Hingegen aus Sicht eines im Äther ruhenden Beobachters läuft eine Uhr dem Signal entgegen, und die andere läuft ihm davon. Die Uhren sind also nicht synchron (Relativität der Gleichzeitigkeit), sondern zeigen nur die Ortszeit 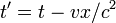$t^{\prime}=t - vx / c^2$ an. Da die bewegten Beobachter aber kein Mittel haben zu entscheiden, ob sie in Bewegung sind oder nicht, werden sie von dem Fehler nichts bemerken. Poincaré verstand daher im Gegensatz zu Lorentz die Ortszeit genauso wie die Längenkontraktion als realen physikalischen Effekt.^[8]

Am 5. Juni 1905 (veröffentlicht am 9. Juni) vereinfachte Poincaré die Gleichungen (welche äquivalent zu denen von Larmor und Lorentz sind) und gab ihnen ihre moderne symmetrische Form, wobei er im Gegensatz zu Larmor und Lorentz die Galilei-Transformation in die neue Transformation direkt integrierte. Poincaré setzte auch die Lichtgeschwindigkeit gleich 1:^[9][10]

$x^{\prime}=\gamma(x-vt),\quad y^{\prime}=y,\quad z^{\prime}=z,\quad t^{\prime}=\gamma\left(t-vx\right)$

und umgekehrt:

$x=\gamma(x^{\prime}+vt^{\prime}),\quad y=y^{\prime},\quad z=z^{\prime},\quad t=\gamma\left(t^{\prime}+vx^{\prime}\right)$

Offenbar war Poincaré die Arbeit von Larmor unbekannt, denn er bezog sich nur auf Lorentz und benutzte deswegen als Erster den Ausdruck "Lorentz Transformation" (wobei der Ausdruck „Lorentz'sche Transformation“ bereits 1900 von Emil Cohn für die 1895-Gleichungen von Lorentz verwendet wurde). Er zeigte, dass Lorentz' Anwendung der Gleichungen das Relativitätsprinzip nicht vollständig erfüllen. Poincaré hingegen konnte neben dem Aufzeigen der Gruppeneigenschaft der Transformation die Lorentzkovarianz der Maxwell-Lorentz-Gleichungen vollständig demonstrieren. Eine deutlich erweiterte Fassung dieser Schrift vom Juli 1905 (veröffentlicht Januar 1906) enthielt die Erkenntnis, dass die Kombination x² + y² + z² − c²t² invariant ist; er führte den Ausdruck 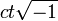$ct \sqrt{-1}$ als vierte Koordinate eines vierdimensionalen Raums ein; er benutzte dabei Vierervektoren bereits vor Minkowski, er zeigte dass die Transformationen eine Konsequenz des Prinzip der kleinsten Wirkung sind und er demonstrierte ausführlicher als vorher deren Gruppeneigenschaft, wobei er den Namen Lorentz-Gruppe („Le groupe de Lorentz“) prägte.

Einstein (1905)

Am 30. Juni 1905 (veröffentlicht September 1905) präsentierte Einstein im Rahmen der speziellen Relativitätstheorie eine radikal neue Interpretation und Herleitung der Transformation, welche nur auf dem Relativitätsprinzip und dem Prinzip der Konstanz der Lichtgeschwindigkeit beruhte. Während Poincaré nur die ursprüngliche lorentzsche Ortszeit von 1895 durch optische Synchronisation abgeleitet hat, konnte Einstein mit einer ähnlichen Synchronisatiosmethode die gesamte Transformation ableiten, und dabei zeigen, dass operationale Überlegungen in Bezug auf Raum und Zeit ausreichten, und kein Äther dafür benötigt wird (ob Einstein von Poincarés Synchronisationsmethode beeinflusst wurde, ist nicht bekannt). Formal war Einsteins Version der Transformation identisch mit der von Poincaré (wobei Einstein jedoch die Lichtgeschwindigkeit nicht gleich 1 setzte):^[11][12][13]

$x^{\prime}=\gamma(x-vt),\quad y^{\prime}=y,\quad z^{\prime}=z,\quad t^{\prime}=\gamma\left(t-x\frac{v}{c^{2}}\right)$

Im Gegensatz zu Lorentz, welcher die Ortszeit nur als mathematischen Trick ansah, zeigte Einstein dass die "effektiven" Koordinaten der Lorentztransformation in der Tat gleichberechtigte Koordinaten von Inertialsystemen sind. Das wurde in gewisser Weise auch schon von Poincaré so dargestellt, jedoch unterschied dieser weiterhin zwischen "wahrer" und "scheinbarer" Zeit.

Siehe auch

Geschichte der speziellen Relativitätstheorie

Lorentzsche Äthertheorie

Lorentz-Transformation

Quellen

Primärquellen

• Einstein, Albert: Zur Elektrodynamik bewegter Körper. In: Annalen der Physik. 322, Nr. 10, 1905, S. 891-921

• Larmor, Joseph: On a Dynamical Theory of the Electric and Luminiferous Medium, Part 3, Relations with material media. In: Philosophical transactions of the Royal society of London. 190, 1897, S. 205-300

• Larmor, Joseph: Aether and Matter. Cambridge: University Press 1900

• Lorentz, Hendrik Antoon: La Théorie electromagnétique de Maxwell et son application aux corps mouvants. In: Archives néerlandaises des sciences exactes et naturelles. 25, 1892a, S. 363–552

• Lorentz, Hendrik Antoon: Die relative Bewegung der Erde und des Äthers. In: Abhandlungen über Theoretische Physik, S. 443-447, Leipzig: B.G. Teubner 1892b/1907

• Lorentz, Hendrik Antoon: Versuch einer Theorie der electrischen und optischen Erscheinungen in bewegten Körpern. Leiden: E.J. Brill 1895

• Lorentz, Hendrik Antoon: Simplified Theory of Electrical and Optical Phenomena in Moving Systems. In: Proceedings of the Royal Netherlands Academy of Arts and Sciences. 1, 1899, S. 427–442

• Lorentz, Hendrik Antoon: Electromagnetic phenomena in a system moving with any velocity smaller than that of light. In: Proceedings of the Royal Netherlands Academy of Arts and Sciences. 6, 1904, S. 809-831

• Lorentz, Hendrik Antoon: The theory of electrons, 2, Leipzig & Berlin: B.G. Teubner 1909/1916

• Poincaré, Henri: La théorie de Lorentz et le principe de réaction. In: Archives néerlandaises des sciences exactes et naturelles. 5, 1900, S. 252–278. Siehe auch deutsche Übersetzung.

• Poincaré, Henri: Sur la dynamique de l'électron. In: Comptes rendus hebdomadaires des séances de l'Académie des sciences. 140, 1905b, S. 1504–1508 Siehe auch deutsche Übersetzung.

• Poincaré, Henri: Sur la dynamique de l'électron. In: Rendiconti del Circolo matematico di Palermo. 21, 1906, S. 129–176 Siehe auch deutsche Übersetzung.

• Voigt, Woldemar: Über das Doppler’sche Princip. In: Nachrichten von der Königl. Gesellschaft der Wissenschaften und der Georg-Augusts-Universität zu Göttingen. Nr. 2, 1887, S. 41-51

Sekundärquellen

• Darrigol, Olivier: Electrodynamics from Ampére to Einstein. Oxford: Clarendon Press 2000, ISBN 0198505949

• Darrigol, Olivier: The Genesis of the theory of relativity. In: Séminaire Poincaré. 1, 2005, S. 1-22

• Janssen, Michel: A Comparison between Lorentz's Ether Theory and Special Relativity in the Light of the Experiments of Trouton and Noble (Thesis) 1995

• Katzir, Shaul: Poincaré’s Relativistic Physics: Its Origins and Nature. In: Physics in perspective. 7, 2005, S. 268–292. doi:10.1007/s00016-004-0234-y

• Macrossan, M. N.: A Note on Relativity Before Einstein. In: The British Journal for the Philosophy of Science. 37, 1986, S. 232-234

• Miller, Arthur I.: Albert Einstein’s special theory of relativity. Emergence (1905) and early interpretation (1905–1911). Reading: Addison–Wesley 1981, ISBN 0-201-04679-2

• Pais, Abraham: "Raffiniert ist der Herrgott ..." : Albert Einstein, eine wissenschaftliche Biographie. Heidelberg: Spektrum 1982/2000, ISBN 3827405297

Einzelnachweise

1. ↑ Miller (1981), 114–115
2. ↑ Pais (1982), Kap. 6b
3. ↑ Miller (1982), Kap. 1.4 & 1.5
4. ↑ Janssen (1995), Kap. 3.1
5. ↑ Macrossan (1986)
6. ↑ Darrigol (2000), Kap. 8.5
7. ↑ Jannsen (1995), Kap. 3.3
8. ↑ Darrigol (2005), Kap. 4
9. ↑ Pais (1982), Kap. 6c
10. ↑ Katzir (2005), 280–288
11. ↑ Miller (1981), Kap. 6
12. ↑ Pais (1982), Kap. 7
13. ↑ Darrigol (2005), Kap. 6