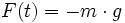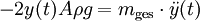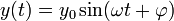- Wasserschwingung
-
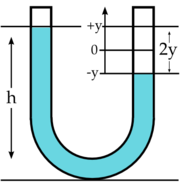
Ein Wasserpendel, auch bekannt als schwingende Wassersäule, ist im Allgemeinen ein U-förmiges Rohr, in dem eine ausgelenkte Wassersäule schwingt.
Die rücktreibende Kraft eines Wasserpendels ist die Gewichtskraft
der überstehenden Wassersäule. Dabei gilt:
m = 2yAρ Masse der überstehenden Wassersäule mges = Aρl Masse der gesamten Wassersäule mit Länge l A = πr2 Querschnittsfläche der Wassersäule ρ Dichte der Flüssigkeit g Fallbeschleunigung Da die Wassersäule schwingt, verändert sich die Höhe der überstehenden Wassersäule in Abhängigkeit von der Zeit. Dadurch verändert sich auch deren Masse und Gewichtskraft. Zum Zeitpunkt t gilt dann:
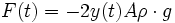 .
.
Mit dem 2. Newtonschen Gesetz,
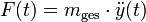 , erhält man die Differentialgleichung
, erhält man die Differentialgleichungbzw.
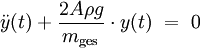 .
.
Die Lösung der Differentialgleichung ist eine harmonische Schwingung, die z. B. durch
gelöst wird. Dabei entspricht y0 der Amplitude, ω = 2πf der Kreisfrequenz und
 die Phase der Schwingung. Der Einfachheit halber wird mit einer Phasenverschiebung von
die Phase der Schwingung. Der Einfachheit halber wird mit einer Phasenverschiebung von 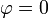 gerechnet, da der Anfangszeitpunkt der Schwingung frei gewählt werden kann.
gerechnet, da der Anfangszeitpunkt der Schwingung frei gewählt werden kann.Durch zweimaliges Ableiten und Einsetzen in die obige Gleichung ergibt sich:
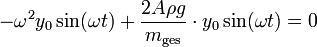 , woraus folgt, dass
, woraus folgt, dass
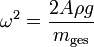 .
.
Dieses Ergebnis kann weiter vereinfacht werden, da mges = Aρl. Es folgt:
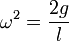 und somit ergibt sich die Kreisfrequenz zu
und somit ergibt sich die Kreisfrequenz zu 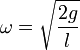 .
.
Für die Periodendauer der Schwingung gilt:
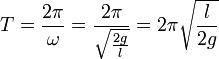 ,
,
die Schwingungsdauer hängt also nur von der Länge der Wassersäule und der Gravitation ab.
Bei einer genaueren Behandlung sind Reibung (Strömungswiderstand) mit der Wand des Rohres und die innere Reibung der Flüssigkeit zu betrachten, die beide die Schwingung dämpfen.
Siehe auch: Pendel, Fadenpendel, Magnetisches Pendel, Federschwingung, Oszillator.
Wikimedia Foundation.