Brownsche Brücke

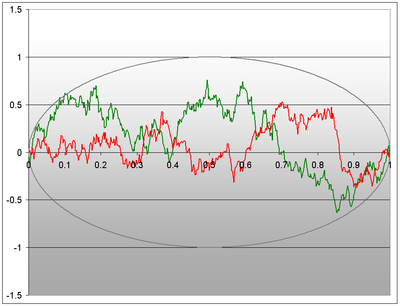Zwei unabhängige brownsche Brücken mit Zeithorizont 1. Als Konfidenzintervall ist grau die doppelte Standardabweichung (Ellipse) mit angegeben

Eine brownsche Brücke ist ein spezieller stochastischer Prozess, der aus dem Wiener-Prozess (auch brownsche Bewegung genannt) hervorgeht. Im Gegensatz zu diesem hat sie aber einen endlichen Zeithorizont mit einem deterministischen (also nicht zufälligen) Endwert, der im Normalfall gleich dem Startwert ist. Die brownsche Brücke wird zur Modellierung von zufälligen Entwicklungen in Daten verwendet, deren Wert aber zu zwei Zeitpunkten bekannt ist.

Definition

Sei $(W_t),\;t\ge 0$ ein Standard-Wiener-Prozess und $T \ge 0$ ein fest gewählter Zeitpunkt. Dann heißt der Prozess

$B_t := (W_t|W_T=0),\;t \in [0,T]$

brownsche Brücke der Länge T. Der einzige Unterschied besteht also darin, dass darauf bedingt wird, dass W zum Zeitpunkt T wieder zur null zurückkehrt. Also ist die Wahrscheinlichkeitsverteilung von B zu jedem Zeitpunkt t gegeben durch die bedingte Wahrscheinlichkeit

$P(B_t \le c)=P(W_t \le c | W_T=0)$.

Insbesondere gilt natürlich B_T = 0. Daher auch der Name des Prozesses: Es wird eine Brücke zwischen 0 und T geschlagen, wo man dann wieder „festen Boden unter den Füßen“ hat.

Eigenschaften

Einige fundamentale Eigenschaften des Wiener-Prozesses bleiben beim Übergang zur brownschen Brücke erhalten, andere jedoch gehen verloren:

• Die brownsche Brücke hat fast sicher überall stetige, nirgends differenzierbare Pfade.
• Die Erwartungswertfunktion der brownschen Brücke ist konstant $t \mapsto E(B_t) = 0$.
• Die Kovarianzfunktion ist $(s,t) \mapsto \operatorname{Cov}(B_s,B_t) = \min(s,t) - \frac{st}{T}$.

Insbesondere gilt also für die Varianz: $\operatorname{Var}(B_t)= t- \frac{t^2}{T}$.

• Die brownsche Brücke ist ein Markov-Prozess, aber im Gegensatz zur brownschen Bewegung weder Lévy-Prozess noch Martingal.
• Die brownsche Brücke ist ein Gauß-Prozess, also durch die obige Erwartungswert- und Kovarianzfunktion bereits eindeutig bestimmt.

Simulation einer brownschen Brücke

Zur Simulation einer brownschen Brücke stehen einem prinzipiell dieselben Möglichkeiten zur Verfügung wie beim Wiener-Prozess, denn aus einem Wiener-Prozess $(W_t),\; t \ge 0$ lässt sich durch $B_t := W_t -\frac{t}{T}W_T$ eine brownsche Brücke mit Zeithorizont T gewinnen. Man kann also einfach eine brownsche Bewegung bis zum Zeitpunkt T simulieren und dann mit obiger Transformation in eine brownsche Brücke umwandeln.

Es bestehen aber noch andere Möglichkeiten: Wird die brownsche Bewegung mittels einer dyadischen Zerlegung (verwirrenderweise wird diese Methode oft ebenfalls als brownsche Brücke bezeichnet) oder Spektralzerlegung erzeugt, so kann man dort einfach den ersten Schritt weglassen, der den Endpunkt W_T bestimmt, und man erhält dann automatisch eine brownsche Brücke. Im Falle der Spektralzerlegung würde die Darstellung also

$B_t = \sum_{k=1}^\infty Z_k \frac{\sqrt{2} \sin(k \pi t)}{k \pi}$ lauten, wobei $Z_1, Z_2, \ldots$ unabhängig standardnormalverteilt sind.

Verallgemeinerte brownsche Brücken

• Alternativ zur obigen Definition, die B_T = 0 garantiert, ist es auch möglich, für jedes beliebige $c \in \R$ durch

$B_t = (W_t|W_T=c), \;t \ge 0$

eine Brücke zu definieren, die auf einem beliebigen, vorher festgelegten Niveau c endet (bildlich gesprochen wird dabei aus der Brücke eine Rampe). Die dazugehörige Transformation lautet dann $B_t=W_t-\frac{t}{T} (W_T-c)$.

• zusätzlich dazu kann man die ursprüngliche brownsche Bewegung auch mit einer beliebigen Volatilität σ versehen (siehe hierzu: verallgemeinerter Wiener-Prozess). Die Formeln für Erwartungswert und Kovarianz lauten dann

$\operatorname{E}(B_t)=\frac{ct}{T}$ beziehungsweise

$\operatorname{Cov}(B_t,B_s) = \sigma^2 \left( \min \{s,t\}-\frac{st}{T} \right)$.

Interessanterweise hat also σ keinen Einfluss auf den Erwartungswert und c keinen auf die Kovarianz. Ein eventueller Drift in der brownschen Bewegung würde die Verteilung des Prozesses überhaupt nicht beeinflussen.