- Airy-Funktion
-
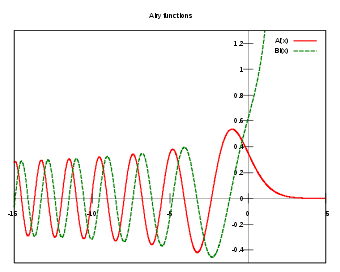
Die Airy-Funktion Ai(x) bezeichnet eine spezielle Funktion in der Mathematik. Die Funktion Ai(x) und die verwandte Funktion Bi(x), die ebenfalls Airy-Funktion genannt wird, sind Lösungen der linearen Differentialgleichung
auch bekannt als Airy-Gleichung. Sie beschreibt unter anderem die Lösung der Schrödinger-Gleichung für einen linearen Potentialtopf.
Die Airy-Funktion ist nach dem britischen Astronomen George Biddell Airy benannt, der diese Funktion in seinen Arbeiten in der Optik verwendete (Airy 1838). Die Bezeichnung Ai(x) wurde von Harold Jeffreys eingeführt.
Inhaltsverzeichnis
Definition
Für reelle Werte x ist die Airy-Funktion als Integral definiert:
Die zweite, linear unabhängige Lösung der Differentialgleichung ist die Airy-Funktion zweiter Art Bi(x):
Werte
Die Airy-Funktionen und ihre Ableitungen haben für x = 0 die folgenden Werte:
Hierbei bezeichnet Γ die Gammafunktion. Es folgt, dass die Wronski-Determinante von Ai(x) und Bi(x) gleich
 ist.
ist.Weitere Darstellungen
unter Verwendung der hypergeometrischen Funktion 0F1.
Für x > 0 lassen sie sich auch mit der modifizierten Bessel-Funktion erster Art I so darstellen:
Eine andere unendliche Integraldarstellung für Ai lautet
Es gibt die Reihendarstellungen[1]
Nullstellen
Die Airy-Funktionen haben nur Nullstellen auf der negativen reellen Achse.[2] Die ungefähre Lage folgt aus dem asymptotischen Verhalten für x→-∞ zu
Asymptotisches Verhalten
Für x gegen +∞ lassen sich Ai(x) und Bi(x) mit Hilfe der WKB-Näherung approximieren:
Für x gegen -∞ gelten die Beziehungen:
Komplexe Argumente
Ai(x) und Bi(x) sind ganze Funktionen. Sie lassen sich also auf der gesamten komplexen Ebene analytisch fortsetzen.
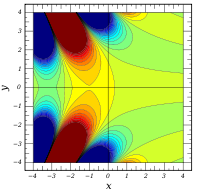
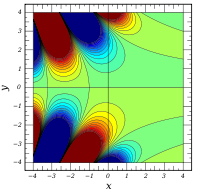
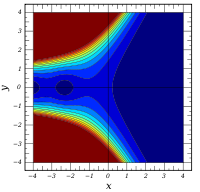
Plots
![\Re \left[ \mathrm{Ai} ( x + iy) \right]](0/aa0b3523b47c6f7f98ba101188331ab8.png)
![\Im \left[ \mathrm{Ai} ( x + iy) \right]](0/a808f8e3b73e8274092ef80fea1609e8.png)

![\mathrm{arg} \left[ \mathrm{Ai} ( x + iy) \right] \,](3/78329bf5b95081ebc42e63a6d56c3383.png)
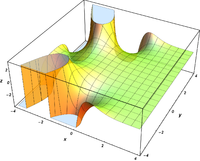
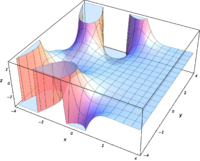
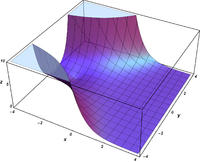
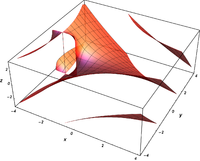
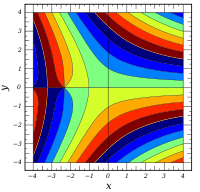
![\Re \left[ \mathrm{Bi} ( x + iy) \right]](3/693594036863615739bfcd90fd329c5a.png)
![\Im \left[ \mathrm{Bi} ( x + iy) \right]](6/3862afac7d69f1b63336e05dd50930b9.png)

![\mathrm{arg} \left[ \mathrm{Bi} ( x + iy) \right] \,](a/1faa5f56c331f6856525b430a1ef980a.png)
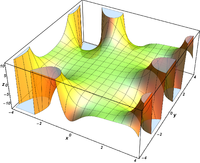
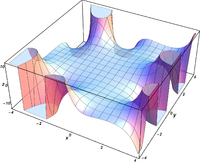
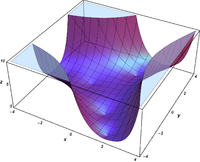
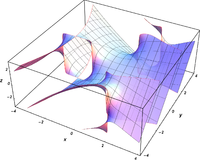
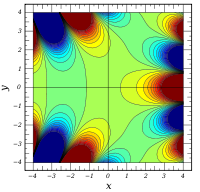
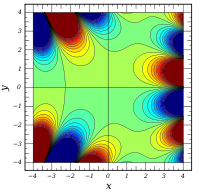
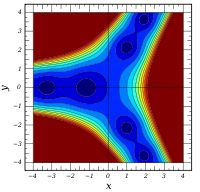
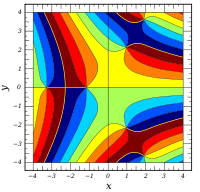
Verwandte Funktionen
Airy-Zeta-Funktion
Zu der Airy-Funktion lässt sich analog zu den anderen Zeta-Funktionen die Airysche Zeta-Funktion definieren als[3]
wobei die Summe über die reellen (negativen) Nullstellen von Ai geht.
Scorersche Funktionen
Manchmal werden auch die beiden weiteren Funktionen Gi(x) und Hi(x) zu den Airy-Funktionen dazugerechnet. Die Integral-Definitionen lauteten[4]
Sie lassen sich auch durch die Funktionen Ai und Bi darstellen.
Literatur
- Milton Abramowitz und Irene A. Stegun: Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. (siehe §10.4). National Bureau of Standards, 1954.
- George Biddell Airy: On the intensity of light in the neighbourhood of a caustic. In: Transactions of the Cambridge Philosophical Society. Band 6, 1838, S. 379—402.
- Olver: Asymptotics and Special Functions, Chapter 11. Academic Press, New York 1974.
Weblinks
 Commons: Airy-Funktion – Sammlung von Bildern, Videos und Audiodateien
Commons: Airy-Funktion – Sammlung von Bildern, Videos und Audiodateien- Eric W. Weisstein: Airy Functions. In: MathWorld. (englisch)
- Bessel, Airy, Struve Functions auf der Wolfram Funktionen Seite
- Chapter AI: Airy and related functions in Digital Library of Mathematical Functions.
Einzelnachweise
- ↑ C. Banderier, P. Flajolet, G. Schaeffer, M. Soria: Planar Maps and Airy Phenomena. In Automata, Languages and Programming. Proceedings of the 27th International Colloquium (ICALP 2000) held at the University of Geneva, Geneva, 9.-15. Juli 2000 (Ed. U. Montanari, J. D. P. Rolim, E. Welzl). Berlin: Springer, S. 388-402, 2000
- ↑ Eric W. Weisstein: Airy Function Zeros. In: MathWorld. (englisch)
- ↑ Eric W. Weisstein: Airy Zeta Function. In: MathWorld. (englisch)
- ↑ Milton Abramowitz und Irene A. Stegun: Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 1954, Seite 447
Wikimedia Foundation.




![\begin{align}
\mathrm{Ai}(0) &{}= \frac{1}{\sqrt[3]{9}\cdot \Gamma(\frac23)}, & \quad \mathrm{Ai}'(0) &{}= -\frac{1}{\sqrt[3]{3}\cdot\Gamma(\frac13)}, \\
\mathrm{Bi}(0) &{}= \frac{1}{\sqrt[6]{3}\cdot\Gamma(\frac23)}, & \quad \mathrm{Bi}'(0) &{}= \frac{\sqrt[6]{3}}{\Gamma(\frac13)}.
\end{align}](9/4499132f02a550c37f28c28cfcb8d187.png)


![\mathrm{Ai}(x)=\frac13\sqrt{x}\left[ I_{-1/3} \left(\frac23x^{3/2}\right) - I_{1/3} \left(\frac23x^{3/2}\right)\right]](9/f994665b2bb2cdc1a4adca204a91af34.png)
![\mathrm{Ai}(x)=\sqrt{\frac x3}\left[ I_{-1/3} \left(\frac23x^{3/2}\right) + I_{1/3} \left(\frac23x^{3/2}\right)\right]](5/5658b3e8af0dfa5ad8512fc5df5c4cab.png)









