Biegelinie

Eine Biegelinie (auch Biegungslinie, Durchbiegungslinie, elastische Linie) ist eine mathematische Kurve, die die Verformung eines Balkens bei Biegung beschreibt. - Es ist in der Statik der Bauwerke die Linie, in die infolge der Elastizität des Baustoffes die Achse eines ursprünglich geradlinigen Balkenträgers übergeht. ^[1]

Die Gleichung der Biegelinie ist ein Teil der Balkentheorie. Sie wird verwendet, um die Durchbiegung prismatischer Balken im Bereich des linear-elastischen Materialverhaltens zu bestimmen. Dabei wird die Annahme zugrunde gelegt, dass die eintretenden Verformungen so klein sind, dass die biegebedingte Veränderung der Balkengeometrie bei der Aufstellung der Gleichung vernachlässigt werden kann. Für den Bereich des nichtlinear-elastischen Materialverhaltens sind Abänderungen erforderlich (vgl. Nichtlineare Stabstatik).

Für kleine Biegewinkel φ gilt die folgende Beziehung zur Durchbiegung w:

${\mathrm dw(x) \over \mathrm dx} = -\varphi(x)$

Hieraus folgt unter Berücksichtigung des Hookeschen Stoffgesetzes eine lineare homogene Differentialgleichung:

$-{\mathrm d\varphi(x) \over \mathrm dx} = {\mathrm d^2 w(x) \over \mathrm dx^2} = w''(x) = -{M_y(x) \over EI_y}$

Durch diese Differentialgleichung ist somit ein Zusammenhang zwischen der Durchbiegung w und dem Biegemoment M_y(x) im Balken gegeben. Dies führt zu drei Gleichungen, für die ein Zusammenhang zwischen der Durchbiegung w und den Schnittlasten im Balken (Biegemoment M_y(x) und Querkraft Q_z(x)) sowie der äußeren Flächenlast q_z(x) gegeben ist. (Die Koordinate x wird hierbei entlang der Balkenachse gezählt. Die Biegung erfolgt um die Koordinaten-Achse y. Die Koordinate z verläuft in Richtung der Querkraft.)

$EI_y\,w''(x) = -M_y(x)$

$EI_y\,w'''(x) = -Q_z(x)$

$EI_y\,w''''(x) = q_z(x)$

Damit die Durchbiegung berechnet werden kann, muss der Elastizitätsmodul E des Materials bekannt sein. Weiterhin muss vorab das Flächenträgheitsmoment I_y des Balkenquerschnitts ermittelt werden. Zusätzlich muss vorab der Verlauf der äußeren Streckenlast q_z(x) oder der Verlauf von Biegemoment M_y(x) oder der Querkraft Q_z(x) bestimmt werden. Die Gleichung kann dann mehrmals integriert werden, bis auf der einen Seite die Durchbiegung w(x) steht. Hierbei ergeben sich mehrere Integrationskonstanten, die durch eine entsprechende Anzahl von Randbedingungen bestimmbar sind.

Das folgende Beispiel zeigt das Vorgehen, wenn vorab der Verlauf des Biegemoments M_y(x) ermittelt wurde und der Elastizitätsmodul und das Flächenträgheitsmoment über die ganze Länge des Balkens als konstant angenommen werden:

$EI_y\,w''(x) = -M_y(x)$

$EI_y\,w'(x) = -\int M_y(x) \mathrm dx + C_1$

$EI_y\,w(x) = -\int \int M_y(x) \mathrm dx + xC_1 + C_2$

Es ergeben sich die zwei unbekannten Konstanten C₁ und C₂. Diese können nun durch zwei Randbedingungen bestimmt werden. Zum Beispiel gilt bei einem Auflager an der Stelle x = a, welches eine Querkraft aufnehmen kann: w(a) = 0. Für ein Auflager an der Stelle x = b, welches ein Moment aufnehmen kann, gilt: w'(b) = 0.

Kreismembran

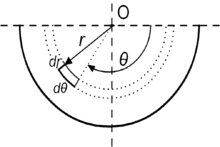
Halbe kreisrunde Membran

Infinitesimales Membranelement

Im Falle einer kreisrunden Membran werden oft auch vereinfacht die Formeln aus der Balkentheorie verwendet. Unter der Annahme einer homogenen Membran wird dann bei rotationssymmetrischen Kräften eine einfache Biegelinie berechnet. Also nur ein Querschnitt der Membran.

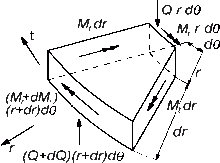
Mit dem tangentialen und radialen Biegemoment M_t und M_r und unter Vernachlässigung von Differentialen höherer Ordnung ergibt sich die Momentgleichung

$M_r + \frac{\mathrm d M_r}{\mathrm dr}\cdot r - M_t + Q \cdot r = 0.$

Die Biegemomente lassen sich über die Poissonzahl μ angeben zu:

$M_r = -D \left( \frac{\mathrm d^2w}{\mathrm dr^2} + \frac{\mu}{r}\frac{\mathrm dw}{\mathrm dr} \right)$

$M_t = -D \left( \mu \frac{\mathrm d^2w}{\mathrm dr^2} + \frac{1}{r}\frac{\mathrm dw}{\mathrm dr} \right)$

D ist hierbei das Widerstandsmoment, das sich über den Elastizitätsmodul E_M der Membran mit Dicke d wie folgt beschreiben lässt:

$D = \frac{E_M\cdot d^3}{12\cdot (1 - \mu^2)}$

Die Biegelinie einer Kreismembran lautet dann in Differentialform, unter Vernachlässigung von kleinen Termen höherer Ordnung sowie von Zugspannungen (nur zulässig für geringe Dehnungen):

$\frac{\mathrm d^3w}{\mathrm dr^3} + \frac{1}{r}\frac{\mathrm d^2w}{\mathrm dr^2} - \frac{1}{r^2}\frac{\mathrm dw}{\mathrm dr} = \frac{Q}{D}$

Nachweise

1. ↑ Otto Lueger, Lexikon der gesamten Technik 1904

Weblinks

•  Wikibooks: Physik des Schlagens/ Biegung des Rohrstocks – Lern- und Lehrmaterialien
• Die Biegelinie
• Zur Biegelinie