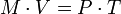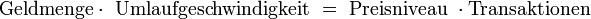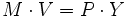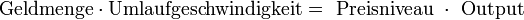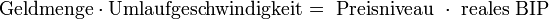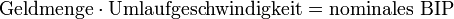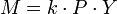Cambridge-Gleichung

Die Quantitätsgleichung ( auch Transaktionsgleichung, Verkehrsgleichung oder Tauschgleichung) liefert Anhaltspunkte über die Beziehung zwischen Geld und Gütertransaktionen innerhalb einer Volkswirtschaft und wird untermauert durch die Quantitätstheorie des Geldes. Neben verschiedenen Formen der Quantitätstheorie gibt es auch verschiedene Formen der Quantitätsgleichung.^[1]

Einordnung

Die Quantitätsgleichung gibt den Sachverhalt wieder, dass in einer Volkswirtschaft bestimmte Transaktionen durchgeführt werden. Sie liegt der Annahme zugrunde, dass alle Transaktionen mittels Geld abgewickelt werden. Anbieter überlassen Eigentumsrechte an Gütern und/ oder Dienstleistungen den Nachfragern, welche im Gegenzug Geld zahlen. Das heißt, mit der Quantitätsgleichung können die wesentlichen Zusammenhänge und Veränderungen der Geld- und Güterseite innerhalb einer Volkswirtschaft dargestellt werden. ^[2]

Geschichte

Die Grundideen der späteren Quantitätstheorie wurden bereits von Jean Bodin erkannt. Aufbauend auf Bodin führte John Locke (englischer Philosoph) den Begriff der Umlaufgeschwindigkeit sowie die Funktion des Geldes als Tauschmittel ein. Locke formulierte somit erstmalig die wesentlichen Elemente der Quantitätstheorie. Diese Idee wurde später von dem schottischen Ökonom David Hume vereinfacht dargestellt und schließlich durch John Stuart Mill erweitert und bekannt gegeben. Die Quantitätsgleichung geht auf Simon Newcomb (1885) zurück und wurde 1911 durch den Ökonomen Irving Fisher präzisiert. Für die Neoquantitätstheorie besonders bedeutend war der Nobelpreisträger Milton Friedman. ^[3]

Die gebräuchlichsten Versionen der Quantitätsgleichung

Transaktionen und Quantitätsgleichung (Transaktionsversion)

Die Quantitätsgleichung stellt eine Identitätsgleichung dar. Sie wird wie folgt definiert:

$M \cdot V =P \cdot T$

$\text{Geldmenge} \cdot \text{ Umlaufgeschwindigkeit } = \text{ Preisniveau } \cdot \text{Transaktionen }$

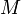$M\,$:Geldmenge

Durchschnittlich umlaufende Menge an Geld innerhalb einer Periode.

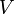$V\,$:Umlaufgeschwindigkeit

gibt an, wie häufig eine Geldeinheit in einer Betrachtungsperiode durchschnittlich verwendet wurde.

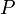$P\,$:Preisniveau

stellt den Durchschnittspreis der Güter und Dienstleistungen dar.

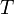$T\,$;Transaktionen

gibt die durchschnittliche Anzahl, der in einer Periode stattfindenden Transaktionen, an.

Während der rechte Teil der Gleichung (P*T) das Volumen der übertragenen Güter und Dienstleistungen (Verkäufe) wiedergibt, stellt die linke Seite (M*V) die Geldmenge dar, die für die Ausübung der Transaktionen nötig ist. Infolge der Tautologie müssen sich beide Seiten entsprechen, d.h. die Summe aller Verkäufe ist gleich der Summe aller Zahlungen.^[4]

Von Transaktionen zum Einkommen (Einkommensversion)

Die Transaktionsform der Quantitätsgleichung wirft jedoch Probleme auf. So ist zum einen die Anzahl der Transaktionen und zum anderen das zugehörige durchschnittliche Preisniveau nicht eindeutig bestimmbar. Aus diesem Grund wurden zur ursprünglichen Quantitätsgleichung Alternativen entwickelt, wie zum Beispiel die Einkommensform der Quantitätsgleichung. In dieser abgewandelten Form wird das Transaktionsvolumen (T) durch die Gesamtproduktion (Output, Y) ersetzt. Diese beiden Größen sind zwar nicht komplett identisch, jedoch sind sie sehr stark miteinander verbunden, da die Menge der ge- und verkauften Waren und Dienstleistungen mit Zunahme der Produktion steigt. Da in der VWL weitere empirische Maße für den Wert Y existieren, entspricht Y ebenso dem realen BIP als auch dem Gesamteinkommen.^[5]

$M \cdot V = P \cdot Y$

$\text{Geldmenge} \cdot \text{Umlaufgeschwindigkeit} = \text{ Preisniveau } \cdot \text{ Output }$

$\text{Geldmenge} \cdot \text{Umlaufgeschwindigkeit} = \text{ Preisniveau } \cdot \text{ reales BIP }$

$\text{Geldmenge} \cdot \text{Umlaufgeschwindigkeit} = \text{nominales BIP}$

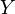$Y\,$: Output/ reales Bruttoinlandsprodukt/ Gesamteinkommen

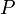$P\,$: Preisniveau

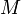$M\,$: Geldmenge

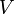$V\,$: Umlaufgeschwindigkeit/ Einkommenskreislaufgeschwindigkeit (Gibt an, wie oft eine Geldeinheit in einer Periode im Durchschnitt zur Zahlung des Einkommens verwendet wird.)

Während der rechte Teil der Gleichung (P*Y) den Wert der produzierten Güter darstellt (nominales Bruttoinlandsprodukt), spiegelt die linke Seite (M*V) die Geldzahlungen wieder, die für den Kauf dieser Güter/ Dienstleistungen benötigt werden.^[6]

Cambridge-Version der Quantitätsgleichung

Eine weitere Version der Quantitätsgleichung beruht auf der Cambridge-Gleichung, welche besagt, dass das Geldangebot dem Produkt aus Nominaleinkommen (P*Y) und durchschnittlicher Kassenhaltungsdauer (k) entspricht.

$M = k \cdot P\cdot Y$

Die uns bereits bekannte Umlaufgeschwindigkeit (V) entspricht nun dem Kehrwert der hier verwendeten durchschnittlichen Kassenhaltungsdauer (k):

$V= \frac{1}{k}$

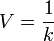
Während V die Umschlagshäufigkeit einer Geldeinheit innerhalb einer Periode darstellt, gibt k die Dauer an, die eine Geldeinheit von einem Wirtschaftssubjekt gehalten wird. Ersetzt man nun in der Cambridge- Gleichung die Kassenhaltungsdauer durch die Umlaufgeschwindigkeit, erhält man nach Umstellen die Quantitätsgleichung. Man kann also sagen, dass die Cambridge- und Quantitätsgleichung prinzipiell identisch sind. Der einzige Unterschied liegt in der Verwendung von Kassenhaltungsdauer und Umlaufgeschwindigkeit.^[7]

Von der Gleichung zur Theorie

Die Quantitätsgleichung stellt noch keine Theorie dar, sie ist jedoch leicht umwandelbar. Dafür sind zwei Annahmen nötig. Zum einen wird T (Transaktionen) bzw. Y(Einkommen) konstant gestellt, da angenommen wird, dass die Menschen einen konstanten Teil ihres Einkommens halten. Zum anderen wird auch V (Umlaufgeschwindigkeit) konstant gesetzt, da diese Variable von einer Vielzahl festgelegter Zahlungsgewohnheiten abhängt (z.B. Löhne, Gehälter, Steuern). Diese ändern sich nur langsam und unterliegen somit keinen kurzfristigen Veränderungen.^{[8] [9]}

Die Quantitätstheorie des Geldes besagt, dass eine Veränderung des Geldangebots (M) eine proportionale Veränderung des Preises zur Folge hat. Es kann darauf geschlossen werden, dass eine Verdopplung der Geldmenge eine Verdopplung des Preises nach sich zieht. Weiterhin beeinflusst die Geldmenge das nominale Einkommen (P*Y).^[10]

Auswirkung einer Geldmengenänderung

Wenn die Geldmenge bei konstanter Umlaufgeschwindigkeit steigt, hat dies zwei mögliche Reaktionen zur Folge. Zum einen kann sich bei noch nicht ausgelasteten Kapazitäten, durch die erhöhte Nachfrage, die Menge der produzierten Güter (reales BIP) erhöhen. Zum anderen bewirkt eine Geldmengensteigerung bei ausgelasteten Kapazitäten eine Preissteigerung, da die hohe Nachfrage auf ein konstantes Güterangebot stößt. Eine Geldmengeninflation tritt auf.

Sinkt die Geldmenge bei konstanter Umlaufgeschwindigkeit, hat dies einen Nachfragerückgang zur Folge, was für die Unternehmen Umsatzrückgänge und Lagerbildung bedeutet und schließlich zu Preissenkungen führen kann.^[11]

Literatur

• N. Gregory Mankiew: Makroökonomie, 4. Auflage, Schäffer Poeschel, Stuttgart, 2000
• Felderer, Homburg: Makroökonomik und neue Makroökonomik, 8. Auflage, Springer Verlag, Berlin2003
• Berlemann: Makroökonomie, „Modellierung, Paradigmen und Politik“, Springer Verlag, Berlin Heidelberg, 2005
• Klatt: Einführung in die Makroökonomie, 2.Auflage,Oldenbourg, München, 1989
• Dornbusch Fischer, Makroökonomik, 6. Auflage, Oldenbourg, Wien, 1995
• R. Clement, W. Terlau: Grundlagen der angewandten Makroökonomie, Verlag Vahlen, München,1998
• Wachtel: Makroökonomie, von der Theorie zur Praxis, Oldenbourg, München 1994
• Gordon: Makroökonomie, 4. Auflage, Oldenbourg Verlag, München1989
• Blanchard/ Illig: Makroökonomie, 4. Auflage, Pearson, München, 2006
• Führmann: Makroökonomie, 3. Auflage, Oldenbourg, München, 1991
• A. Wagner: Makroökonomie, 2. Auflage, Lucius& Lucius, Stuttgart, 1998

Belege

1. ↑ Vgl.: N. Gregory Mankiew, Makroökonomie 4. Auflage, Schäffer Poeschel, Stuttgart,2000, Seite 185
2. ↑ Vgl.: Berlemann, Makroökonomie, „Modellierung, Paradigmen und Politik“, Springer Verlag, Berlin Heidelberg, 2005, Seite 269
3. ↑ Vgl.: http://de.wikipedia.org/wiki/Quantitätstheorie
4. ↑ Vgl.: N. Gregory Mankiew, Makroökonomie 4. Auflage, Schäffer Poeschel, Stuttgart,2000, Seite 185
5. ↑ Vgl.: N. Gregory Mankiew, Makroökonomie 4. Auflage, Schäffer Poeschel, Stuttgart,2000, Seite 185
6. ↑ Vgl.: N. Gregory Mankiew, Makroökonomie 4. Auflage, Schäffer Poeschel, Stuttgart,2000, Seite 185
7. ↑ Vgl.: Felderer, Homburg, Makroökonomik und neue Makroökonomik, 8. Auflage, Springer Verlag, Berlin2003, Seite 80.
8. ↑ Vgl.: Gordon, Makroökonomie 4. Auflage, Oldenbourg Verlag, München1989, Seite 466 f
9. ↑ Vgl.: Felderer, Homburg, Makroökonomik und neue Makroökonomik, 8. Auflage, Springer Verlag, Berlin2003, Seite 81.
10. ↑ Vgl.: R. Clement, W. Terlau, Grundlagen der angewandten Makroökonomie, Verlag Vahlen, München 1998, Seite111.
11. ↑ Vgl.: R. Clement, W. Terlau, Grundlagen der angewandten Makroökonomie, Verlag Vahlen, München,1998, Seite 110