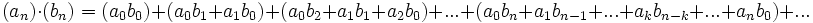- Cauchy-Produkt
-
Die Cauchy-Produktformel, auch Cauchy-Produkt oder Cauchy-Faltung, benannt nach dem französischen Mathematiker Augustin Louis Cauchy gestattet die Multiplikation und Division unendlicher Reihen.
Sind
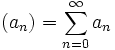 und
und 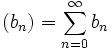 zwei absolut konvergente Reihen, so ist deren Produkt
zwei absolut konvergente Reihen, so ist deren Produkt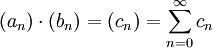 , mit
, mit 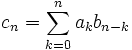
wiederum eine absolut konvergente Reihe.
Nach dem Satz von Mertens ist es schon ausreichend zu fordern, dass mindestens eine der konvergenten Reihen (an) und (bn) absolut konvergiert, damit das Cauchyprodukt (cn) konvergiert (nicht notwendigerweise absolut) und mit
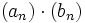 übereinstimmt.
übereinstimmt.Konvergieren die Reihen (an) und (bn) nur bedingt, so kann es sein, dass das Cauchyprodukt (cn) nicht konvergiert.
Beispiel
Es soll das Produkt
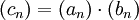 der beiden Reihen
der beiden Reihengebildet werden.
Es gilt
Die cn konvergieren für
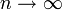 mit der Substitution
mit der Substitution 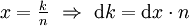 betragsmäßig gegen das Integral
betragsmäßig gegen das IntegralNach Trivialkriterium divergiert daher (cn).
Wenn jedoch (an) und (bn) beide bedingt konvergieren und das Cauchyprodukt (cn) konvergiert, dann stimmt es nach einem Satz von Abel mit
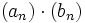 überein.
überein.Schreibt man diese Formel aus, so erhält man:
Bricht man diese Reihe bei einem gewissen Wert von n ab, so erhält man eine Näherung für das gesuchte Produkt.
Werden insbesondere Potenzreihen multipliziert, d.h., sind
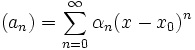 und
und 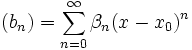 , so gilt für ihr Produkt
, so gilt für ihr Produkt 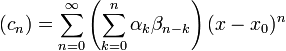 , womit die Produktreihe nach Potenzen von x geordnet werden kann.
, womit die Produktreihe nach Potenzen von x geordnet werden kann.Um dagegen die Reihe
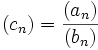 aufzufinden, bildet man
aufzufinden, bildet man 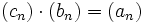 für unbekannte cn und ermittelt diese mit Hilfe eines Koeffizientenvergleichs.
für unbekannte cn und ermittelt diese mit Hilfe eines Koeffizientenvergleichs.Zahlenbeispiel
1/81 = 1/9 * 1/9 = 0,11111... * 0,11111... = 0,0 (1) * (1+1) * (1+1+1) * (1+1+1+1) * (1+1+1+1+1)...
0,11111... * 0,11111...0 011111... 011111... 011111... 011111...
0,012345... = 0,0123456789(10)(11)(12)(13)...
1/81 liefert als Ergebnis somit alle fortlaufenden Zahlen. Diese ungewöhnliche Darstellung ist im Dezimalsystem allerdings so nicht darstellbar, da es nur 10 Zahlen (0-9) umfasst. Die (10) vergrößert die vorstehende 9 zu einer 10, sodass die 8 zu einer 9 aufgerundet wird.
Wikimedia Foundation.

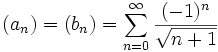
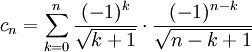
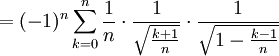
![\int_0^1 \frac{1}{\sqrt{x}\,\sqrt{1-x}}\, dx =\int_0^1 \frac{2\, dz}{\sqrt{1-z^2}}=2 \left[\arcsin z\right]_0^1=\pi>0](/pictures/dewiki/51/3360f94e65f8ac2e86b7fa38b06164a3.png)