Abstraktion (Geoinformatik)

Das Wort Abstraktion (lat. abstractus – „abgezogen“, Partizip Perfekt Passiv von abs-trahere – „abziehen, entfernen, trennen“) bezeichnet meist den induktiven Denkprozess des Weglassens von Einzelheiten und des Überführens auf etwas Allgemeineres oder Einfacheres. Daneben gibt es spezifische Verwendungen von Abstraktion in bestimmten Einzelwissenschaften und einzelnen Theorien.

Philosophie

In der Philosophie bezeichnet Abstraktion oft eine Operation des Denkens, welche von konkreten Objekten der Wirklichkeit (etwa dieser Baum hier, jener Baum dort usw.) allgemeine Eigenschaften „abzieht“ und daraus beispielsweise allgemeine Begriffe formt (etwa: die Gattung Baum). Dazu muss offenbar von bestimmten individuellen Eigenschaften der konkreten Objekte abgesehen werden, sodass die abstrahierten Merkmale auf mehrere andere Objekte auch zutreffen. Solchen allgemeinen Begriffen sprechen einige Philosophen (sogenannte Universalienrealisten) unabhängige Realität zu (es gibt den Begriff Baum auch dann, wenn es keine Bäume in der wirklichen Welt gibt oder keine Worte in irgendeiner natürlichen Sprache gibt, welche den Gehalt des Baum-Begriffs ausdrücken). Solche Begriffe haben, meinen einige Theoretiker, eben weil sie Abstraktionen sind, einen spezifischen Eigenstatus, wie er informationellen Gehalten überhaupt zukommt: nämlich seien diese Gehalte nicht raumzeitlich lokalisiert und seien nur solchen Bewusstseinen zugänglich, welche Abstraktionsleistungen des entsprechenden Typs überhaupt vollziehen können. Letzteres nähert sich sogenannten idealistischen oder konstruktivistischen Positionen bezüglich abstrakter Begriffe. Dies sind Gegenpositionen zum Universalienrealismus, welche behaupten, dass Allgemeinbegriffe und dergleichen bloße Konstrukte sind und kein Sein unabhängig von Denk- bzw. genauer Abstraktionsoperationen haben. (Außerdem nennt man diejenigen extremen Positionen, welche lehren, dass es überhaupt nur einen Typ von Seiendem gebe, nämlich eben mentales, als Gedachtes, meist ebenfalls idealistisch.) Debatten über derartige ontologische und erkenntnistheoretische Themen werden seit Jahrhunderten geführt und haben in den letzten Jahrzehnten an Komplexität nochmals zugenommen. So wurden beispielsweise unterschiedliche realistische Theorien bezüglich natürlicher Arten (Objekten wie Wasserstoff, Bäume etc.) ausgearbeitet; es gibt sog. trope-Theorien, welche Universalien als nur, aber vollständig in Individuen existent beschreiben. Erstere Art von Theorien verneint, dass über korrekte Abstraktionleistungen gewonnene Artbegriffe bloße Abstraktionen sind. Auch um die intuitiv plausible, aber schwer exakt zu explizierende Unterscheidung von abstrakten und konkreten Objekten einzufangen, wurden komplizierte Theorien ausgearbeitet, etwa von Crispin Wright und Bob Hale oder von Edward Zalta. Während Theoretiker wie George Bealer die notwendige Existenz abstrakter Objekte a priori und Hilary Putnam auf wissenschaftstheoretischer Basis zu zeigen versuchen, will etwa Hartry Field das Gegenteil beweisen, insbesondere für die Philosophie der Mathematik.

Ausgewählte Positionen der Philosophiegeschichte

Schon die Vorsokratiker suchten nach einem Urstoff oder mehreren, um die Realität durch Rückführung auf abstrakte Objekte oder Prinzipien zu erklären. Heraklit beispielsweise hat in allem Seienden nach dem Gemeinsamen gesucht.

Platon legt jedem Ding eine vollkommene Idee des Gegenstandes zugrunde: dieser Baum ist deswegen ein Baum, weil er teilhat an der Idee des Baumes, welche selbst nicht raumzeitlich lokalisiert ist und auch nicht einfach nur durch Abstraktion, sondern durch Wiedererinnerung an die Idee des Baumes erkannt wird. Die mit einem solchen Ideenrealismus verbundenen Probleme wurden teilweise auch von Platon selbst schon diskutiert.

Aristoteles diskutiert die platonische Ideenlehre wesentlich kritischer. Er selbst arbeitet mit dem Begriff eidos. Dabei handelt es sich um eine Art Strukturprinzip von Objekten eines je bestimmten Typs. Dieses aber ist selbst im Seienden lokalisiert und metaphysisch nicht von ihm separierbar (es gibt keine Röte, wenn es keine roten Objekte gibt). Aristoteles lehrt allerdings auch eine Vierheit von Ursachen. Besonders die Form-Ursache ist hier einschlägig. Durch Rückführung auf basalere, abstraktere Ursachen werden ebenfalls Objekte und ihre So-Beschaffenheit erklärt. Da diese Rückführung nicht unenendlich weitergehen soll, setzt Aristoteles einen selbst „unbewegten Beweger“ an. Alle „Bewegung“, was insbesondere jede Veränderung in Lage und Beschaffenheit meint, hat in ihm ihre erste Ursache.

Von dem spätantiken Philosophen Boëthius stammt die Gegenüberstellung von abstrakt und konkret.

Der sogenannte Universalienstreit darüber, ob die abstrakten Begriffe „vor“ oder „nach den Dingen“ vorhanden seien bzw. gebildet würden, hielt die Denker des Mittelalters in Atem.

Johannes Duns Scotus beispielsweise ging bei seiner „abstraktiven“ Erkenntnislehre davon aus, dass ein Gegenstand nur durch die Sinne erfahrbar ist und im Verstand ein Bild erzeugt. Durch die unabhängige, aktive Tätigkeit des Verstandes wird diese noch ungeordnete Vorstellung als das Universelle im Abbild bestimmt. Das heißt, das im Bild enthaltene Allgemeine wird von den speziellen und stofflichen Bedingungen des individuellen Gegenstandes abstrahiert. Es entsteht die deutlich abgegrenzte Erkenntnis, die den Gegenstand begrifflich in allen seinen Facetten erfasst. Die Erkenntnis wird erst abgeschlossen, wenn sie im Gedächtnis verankert ist. Erst durch die (passive) Verinnerlichung wird ein Gegenstand intelligibel und kann als Möglichkeit in der Vergegenwärtigung aufleuchten, das heißt wieder in das Bewusstsein gerufen werden. Der einmal gewonnene Begriff eines Gegenstandes kann durch einen anderen Begriff ersetzt werden, wie auch Vorstellungen durch Kombination verändert oder neu erzeugt werden können.

Auch einige englische Philosophen der frühen Neuzeit, z. B. Locke und Berkeley (letzterer trieb die Abstraktion bis zum nicht mehr hintergehbaren „something“) sowie Leibniz, Spinoza und Descartes waren mit der Thematik befasst und stritten u. a. darum, ob unsere Begriffe von Essentien (das, was etwa Wasser als solches ausmacht bzw.zu Wasser macht) angeboren oder erworben sind.

An diesem Streit beteiligte sich auch Hume, der einen empiristischen Ansatz vertrat; Ursache und Wirkung beispielsweise wären lediglich aus der Erfahrung einer Folge von etwas auf etwas gebildet, jedoch wüssten wir niemals mit Sicherheit, ob morgen die Sonne wieder aufgehen werde. Hume wurde wiederum von Kant kritisiert, der das Gegenkonzept der (vorauszusetzenden) „Bedingungen einer jeden Erfahrung“ entwickelte: die reinen Formen der Anschauung, die Kategorien des Verstandes, die Regulative der Vernunft.

Die philosophische Bewegung des sogenannten deutschen Idealismus um die Wende vom 18. zum 19. Jahrhundert (z. B. Hegel, Schelling) bestimmte als Gegenbegriff zur Abstraktion den sehr voraussetzungsreichen Begriff der Konkretion. Diese Theorien sind sehr kompliziert. Die Idealisten verstanden unter Konkretion nicht den Vorgang, das (landläufige) Konkrete zu denken oder einen (landläufigen) Allgemeinbegriff auf etwas Konkretes anzuwenden, sondern die „dialektische Aufhebung“ des Unterschiedes von Abstraktem und Konkretem in einer höheren Einheit, die nach ihren Angaben erst ermöglichen sollte, die Wirklichkeit angemessen zu erfassen.

Heidegger, der in Sein und Zeit (1927) der gesamten Denktradition und insbesondere den Idealisten vorwarf, die „Alltäglichkeit“ übersprungen zu haben, bildete ein anderes Gegensatzpaar, das Abstraktion und Konkretion der „Alltäglichkeit“ fassen sollte: „Zuhandenheit“ und „Vorhandenheit“.

Im „Philosophischen Wörterbuch“ (Apel/Ludz, 1958) wird Abstraktion als Gegensatz zur Determination gesehen, also ganz anders als z. B. bei den Idealisten, und eine Reihe verschiedener Abstraktionsmethoden aufgezählt: isolierende oder generalisierende (verallgemeinernde), quantitative oder qualitative, negative oder positive Abstraktion.

Die verschiedenen Auffassungen der Erkenntnistheorie ergeben unterschiedliche Definitionsansätze von Abstraktion. Auch die Vertreter moderner Wissenschaftstheorie und analytischer Philosophie beteiligten sich an diesem Disput.

Auch der Terminus Konkretisierung wird der Abstraktion gegenüber gestellt.

Einmütigkeit der Auffassungen ist nicht erreicht worden. Lediglich darüber herrscht seit alters Einigkeit, auch unter den Philosophen, dass Mathematik und Logik rein abstrakte Wissenschaften seien. Heute gilt auch die Systemtheorie der Informatik als rein abstrakte Wissenschaft.

Andere Wissenschaften lassen sich unter anderem aus abstrakter Sicht betrachten. In der Kunst bezeichnet man Werke als abstrakt, die sich von der gegenständlichen Sichtweise entfernen.

Kunst

In der Bildenden Kunst bezeichnet Abstraktion einerseits die mehr oder weniger ausgeprägte stilistische Reduzierung der dargestellten Dinge auf wesentliche oder bestimmte Aspekte. In diesem Fall spricht man davon, dass vom Allgemeinen auf das Wesentliche abstrahiert wird. Was als wesentlich gilt, bestimmt einerseits die Kreativität des Künstlers, andererseits die Wahrnehmung des Betrachters.

Die Abbildungen vergleichen realistischere und abstraktere Zeichnungen eines Hirschkäfers. Durch Abstraktion können Veränderungen zum Beispiel in Perspektive, Farbgebung, Struktur oder Stil entstehen. Besonders auffällig sind oft Merkmalsveränderungen, das heißt Dinge, die wie die gelbe Fläche im Beispiel F nicht zum Objekt gehören oder wie die zusätzlichen Beinglieder im Beispiel D ein Merkmal betonen.

A realistischere Zeichnung; Form, Perspektive und Merkmale sind erhalten aber Farbe verändert	B realistischere Zeichnung; aber Konturen betont, Merkmale sind erhalten	C realistischere Zeichnung; aber Farbe verändert, Merkmale sind erhalten
D abstraktere Zeichnung; Form und Farbe noch erhalten, aber Merkmal Beinglieder betont, Perspektive ansatzweise noch erhalten	E abstraktere Zeichnung; Form, Farbe und Perspektive sind verändert	F abstraktere Zeichnung; Form, Farbe und Merkmale sind verändert, Perspektive ist völlig aufgegeben

Andererseits bezeichnet der Begriff in der Kunst verschiedene Strömungen der Moderne oder der zeitgenössischen Kunst, deren Merkmal sogar die völlige Abwesenheit eines konkreten Gegenstandsbezuges ist. (Abstrakte Kunst, insbesondere Abstrakte Malerei) Hierbei muss der Betrachter seine individuelle Fähigkeit zur Abstraktion zunehmend erweitern, um die vom Künstler gemachten Veränderungen noch nachvollziehen zu können. Werke dieser Strömungen thematisieren beispielsweise die formalen Gestaltungsprinzipien selbst (Geometrische Abstraktion in der gestaltenden Kunst), die Gebärdensprache des Künstlers (Action Painting) oder auch die farblichen Veränderungen (Informel, Tachismus, Drip Painting). Auch in der darstellenden Kunst kann die Abstraktion so weit gehen, dass die ursprünglichen Merkmale (z. B. eines Gesprächs oder einer Handlung) vom Betrachter nur dann verstanden werden, wenn er das Wesentliche darin erkennt. Alle Strömungen der abstrakten Kunst erfordern Wahrnehmungs- und Interpretationsfähigkeiten.

Mathematik

In der Mathematik und der neueren Philosophie werden Abstrakta meist mit Äquivalenzklassen identifiziert. Ausgehend von einer gegebenen Menge K von Konkreta sowie einer auf ihr erklärten Äquivalenzrelation ~ (einer reflexiven, transitiven und symmetrischen zweistelligen Relation) wird ein Abstraktum einfach als die Menge derjenigen Konkreta aufgefasst, die zueinander in der Relation ~ stehen. Gemeinsam ist allen Varianten der modernen Abstraktionstheorie der Grundgedanke, dass von der zwischen den Konkreta bestehenden Äquivalenzrelation ~ (einer „generischen“ oder „qualitativen Gleichheit“) zur Identität („numerischen Gleichheit“) der jeweiligen Abstrakta übergegangen werden soll. Anhand einer Liste von Beispielen wird dies klarer:

• gleichschwere Körper haben dasselbe Gewicht;
• gleichmächtige Mengen haben dieselbe Kardinalzahl;
• parallele Geraden haben dieselbe Richtung;
• synonyme Prädikate drücken denselben Begriff aus.

Körper, Mengen, Gerade und Prädikate sind in dieser Liste die Konkreta K; Gewichte, Kardinalzahlen, Richtungen und Begriffe sind die aus ihnen gewonnenen Abstrakta; „gleichschwer“, „gleichmächtig“, „parallel“, „synonym“ drücken die Äquivalenzrelation ~ aus. Für den Fall der Anzahlen ist dies bereits von David Hume in seinem Treatise of Human Nature formuliert worden, man spricht deshalb auch von Hume’s principle.

Aus dieser Liste lässt sich ein allgemeines Schema gewinnen: 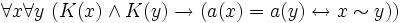$\forall x \forall y\ (K(x) \land K(y) \rightarrow (a(x) = a(y) \leftrightarrow x \thicksim y))$; lies: Für alle Konkreta x und y ist das Abstraktum a zu x identisch mit dem Abstraktum a zu y genau dann, wenn x in ~ zu y steht. Gottlob Frege hat dies in seinen Grundlagen der Arithmetik als eine Umverteilung beschrieben: Der Inhalt von z. B. „parallel“ wandert z. T. in das allgemeine „=“, z. T. in den abstraktiven Funktor a.^[1]

Dies taugt jedoch nicht als Definition des Funktors a. Freges origineller Vorschlag aus den Grundlagen der Arithmetik besteht deshalb darin, als das Abstraktum zu einer gegebenen Äquivalenzrelation einfach die zugehörige Äquivalenzklasse anzusehen. Für den Fall der Anzahlen gibt er die berühmte Definition:

Die Anzahl, welche dem Begriffe F zukommt, ist der Umfang des Begriffes „gleichzahlig dem Begriffe F“.^[2]

Verallgemeinert und in moderne Notation überführt, lässt sich einfach festhalten: 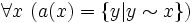$\forall x \ (a(x) = \{y | y \thicksim x\})$. In Worten: Das Abstraktum zu x unter einer gegebenen Äquivalenzrelation ~ ist die Menge derjenigen y, die in der Äquivalenzrelation ~ zu x stehen.

Psychologie

In der Psychologie bezeichnet man als Abstraktion jenen Prozess, der Informationen so weit auf ihre wesentlichen Eigenschaften herab setzt, dass sie psychisch überhaupt weiter verarbeitet werden können. So wird beispielsweise im Alltag jede Form von Stuhl in jeder Situation völlig anders wahrgenommen (Perspektive, Form), aber im Sprachverhalten auf ihre dem Menschen dienliche Eigenschaft reduziert. (Sitzgegenstand mit nur locker umrissener Formgebung) So kann beispielsweise die Aufforderung „Gib mir bitte einen Stuhl!“ überhaupt verstanden werden, weil der Auffordernde und der Empfänger eine gemeinsame, abstrakte Vorstellung darüber haben, was für den jeweiligen Zweck benötigt wird.

Abstraktionsfähigkeit ist in der Psychologie die Voraussetzung für die Bildung von Begriffen und Regeln und damit die Voraussetzung für kognitive Fähigkeiten wie Denken, Lernen, Perzeption oder Gedächtnis. Zur Vereinfachung werden deshalb Begriffe oft in Enzyklopädien oder Wörterbüchern gesammelt und definiert. Die größere Menge aller Begriffe wird jedoch individuell erzeugt, sie sind nur situativ bedeutsam.

Die Begriffsbildung durch Abstraktion wird als wesentliche individuelle und kulturelle Fähigkeit beschrieben. Ein Mensch wie Borges fiktionaler Charakter Funes, der jede Sekunde seines Lebens als neu und einzigartig erlebt, wäre nicht überlebensfähig.^[3]

Die Abstraktionsstufe von Begriffen (im bildlichen Bereich icon genannt) kann unterschiedlich hoch sein. Das menschliche Gehirn arbeitet optimal mit Begriffen auf einer mittleren Abstraktionsstufe, die weder zu allgemein, also uninformativ (Beispiel: "Gib mir mal das Ding!"), noch zu speziell, also mit unwichtigen Details belastet ist.^[4] Vorteile dieser moderately abstract conceptual representations (Zeitz) sind:

1. sie sind im Langzeitgedächtnis stabil, werden also durch neue Detailinformationen nicht gleich ungültig
2. sie sind fruchtbar, weil sie weder von jedem, noch ausschließlich von ganz speziellen Hinweisreizen aktiviert werden
3. sie können leicht an die gegebene Situation angepasst werden.

Zahlreiche Studien zeigten, dass Menschen im allgemeinen mit drei Abstraktionsstufen pro Begriff auskommen: der mittleren Grundstufe (z. B. „Stuhl“), plus einem abstrakteren Oberbegriff (z. B. „Möbel“) und der konkreteren Stufe der Einzelbeispiele (z. B. „mein Küchenstuhl“).^[5] Die Begriffe der Grundstufe zeichnen sich durch charakteristische Eigenschaften aus:

1. Sie werden von Kindern als erste gelernt (z. B. erst „Uhr“, später „Messgerät“ und „Armbanduhr“).
2. Der Umgang mit ihnen erfordert oft spezielle Bewegungsabläufe (Das „Daraufsetzen“ ist bei allen Stühlen ähnlich).
3. Sie sehen ungefähr gleich aus, so kann die ganze Kategorie im Gedächtnis durch ein einziges Bild repräsentiert werden (vgl. die Bilderbücher für Kleinkinder).

Mit zunehmender Erfahrung ändert sich die Belegung der drei Abstraktionsstufen, so wird ein Möbelverkäufer sich nicht an jeden einzelnen Stuhl erinnern, jedoch die Preisklassen zur Unterscheidung heranziehen.

Abstraktionsfähigkeit ist außerdem eine wichtige Voraussetzung für effektives und effizientes Lernen. In der Lernpsychologie gibt es daher den Begriff der „progressiven Abstraktion“, d. h. die Fähigkeit, gleichartige Informationen mehr und mehr unter bestimmten Oberbegriffen zusammenfassen zu können und somit sein Wissen immer engmaschiger zu vernetzen.

Die Abstraktionsfähigkeit als psychische Leistung kann auch pathologisch gestört sein. So können Personen mit verschiedenen Formen der Schizophrenie, mit schweren Neurosen oder mit einer Intelligenzminderung Probleme haben, Begriffe zu verstehen oder auseinander zu halten. Sie haben oft in sozialen Interaktionen Defizite. Bei einer Intelligenzminderung können beispielsweise Begriffe wie „Leiter“ und „Treppe“ nicht mehr abstrakt von einander unterschieden werden. Personen mit Abstraktionsdefiziten beschreiben beispielsweise diese Gegenstände oft mit „da kann man hoch steigen“, statt Unterschiede in Transportabilität oder Steigungswinkel zu erkennen. Insbesondere typisch für eine mangelnde Abstraktionsfähigkeit ist das Unvermögen, einen konkreten Gegenstand, z.B. „Treppe in meinem Haus in der Musterstraße 3“ als funktionsgleich mit allen anderen „Treppen“ zu erkennen.

Abstraktion in der Tiefenpsychologie

C.G. Jung definiert Abstraktion als eine Geistestätigkeit, die einmalige, unvergleichliche oder individuelle Inhalte aus einer Verknüpfung wegzieht, differenziert. Wenn man zum Objekt abstrahierend eingestellt ist, wird versucht, sich des Objekts als einzigartigen Ganzen zu entledigen und das Interesse vom Objekt abzuziehen und auf das Subjekt zurückfließen zu lassen. Laut Jung ist Abstraktion eine Zurückziehung der Libido (=Energie) vom Objekt zum subjektiven abstrakten Inhalt, was einer Objektentwertung gleich kommt. Anders gesagt ist Abstraktion eine introvertierte Libidobewegung.

Sprachwissenschaft

Eine sprachliche Abstraktion ist die Bildung von Kategorien (Taxonomie), die nicht die Einzelobjekte beschreiben. Es wird dabei eine abstrakte Kategorie gebildet, die Eigenschaften der Einzelobjekte integriert, diese aber nicht genau benennt. Die Kategorie „Einrichtungsgegenstände“ ist eine Abstraktion der konkreten Begrifflichkeiten „Sofa“, „Tisch“, „Schrank“, „Lampe“ usw., die von der Kategorie „Einrichtungsgegenstände“ umfasst werden.

Siehe hierzu auch: Superierung

Die Abstraktion in grammatische Kategorien wie Adverbien, Adjektive, Substantive, Prädikat, Kopula, ist eine erweiterte Denkleistung, die Kleinkindern nicht zugänglich ist. Im Alltag vollzieht sich dieser Abstraktionsprozess unwillkürlich und unbemerkt. Die Menschwerdung hing entscheidend mit der Entwicklung der Fähigkeit zur gedanklichen Abstraktion zusammen. Darüber jedoch, was genau unter Abstraktion zu verstehen ist, waren und sind sich Denker und Wissenschaftler nicht immer einig.

Nachweise

1. ↑ Gottlob Frege: Die Grundlagen der Arithmetik. Breslau 1884, § 64. Vgl. Geo Siegwart: Abstraktion unter einer Gleichheit, in: Hans Jörg Sandkühler (Hrsg.): Enzyklopädie Philosophie. Hamburg: Meiner, 1999
2. ↑ Frege, Grundlagen der Arithmetik, S. 79f.
3. ↑ Jorge Luis Borges: Funes el memorioso (1942, dt. „Das unerbittliche Gedächtnis“)
4. ↑ C.M. Zeitz: Some concrete advantages of abstraction, in: P.J. Feltovich et. al. (Eds.): Expertise in context. MIT Press, Cambridge (Mass.), 1997
5. ↑ M. Eysenck, M. Keane: Cognitive Psychology. Psychology Press, Hove (UK), 2000

Siehe auch

• Holismus, Reduktionismus, Formalismus (Kunstgeschichte), Induktion, Deduktion, Synonymie, Universalienproblem

Im Computerbereich:

• Hardware Abstraction Layer, Objektorientierte Programmierung, Generalisierung (UML)

Literatur

• Frege, G.: Die Grundlagen der Arithmetik. Breslau 1884
• Siegwart, G.: Abstraktion unter einer Gleichheit, in: H. J. Sandkühler (Hrsg.): Enzyklopädie Philosophie, Hamburg 1999.
• Thiel, Chr.: Gottlob Frege: Die Abstraktion. In: J. Speck (Hg.): Grundprobleme der großen Philosophen. Philosophie der Gegenwart I. Göttingen 1972, 9–44.

Weblinks

• Eintrag in der Stanford Encyclopedia of Philosophy (englisch, inklusive Literaturangaben)Vorlage:SEP/Wartung/Parameter 1 und weder Parameter 2 noch Parameter 3
• Eintrag im Dictionary of the History of Ideas (englisch, inkl. Literaturangaben)