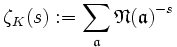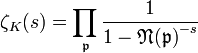Dedekindsche ψ-Funktion — Dieser Artikel wurde auf der Qualitätssicherungsseite des Portals Mathematik eingetragen. Dies geschieht, um die Qualität der Artikel aus dem Themengebiet Mathematik auf ein akzeptables Niveau zu bringen. Dabei werden Artikel gelöscht, die nicht… … Deutsch Wikipedia
Dedekindsche Eta-Funktion — Die Dedekindsche η Funktion in der komplexen Ebene Die nach dem deutschen Mathematiker Richard Dedekind benannte η Funktion ist eine auf der oberen Halbebene holomorphe Funktion. Sie spielt eine wichtige Rolle in der Theorie d … Deutsch Wikipedia
Dedekindsche Zeta-Funktion — Die Dedekindsche Zeta Funktion eines Zahlkörpers K ist definiert als wobei die ganzen Ideale des Zahlkörpers K durchläuft und deren Absolutnorm ist. Die Reihe ζK(s) ist absolut und gleichmäßig konvergent im Bereich … Deutsch Wikipedia
Dedekindsche Psi-Funktion — Die Dedekindsche ψ Funktion (nach Richard Dedekind) ist eine multiplikative zahlentheoretische Funktion. Sie ist nicht zu verwechseln mit anderen dedekindschen Funktionen und wird mit dem kleinen griechischen Buchstaben psi (ψ) bezeichnet. Für… … Deutsch Wikipedia
Dedekindsche η-Funktion — Die Dedekindsche η Funktion in der komplexen Ebene Die nach dem deutschen Mathematiker Richard Dedekind benannte η Funktion ist eine auf der oberen Halbebene holomorphe Funktion. Sie spielt eine wichtige Rolle in der Theor … Deutsch Wikipedia
Dedekindsche Funktion — In der Zahlentheorie werden mehrere Funktionen nach Richard Dedekind benannt: Dedekindsche Zeta Funktion Dedekindsche Eta Funktion Dedekindsche Psi Funktion Diese Seite ist eine Begriffsklärung z … Deutsch Wikipedia
Dedekind-Funktion — In der Zahlentheorie werden mehrere Funktionen nach Richard Dedekind benannt: Dedekindsche Zeta Funktion Dedekindsche Eta Funktion Dedekindsche Psi Funktion … Deutsch Wikipedia
Arithmetische Funktion — Eine zahlentheoretische oder auch arithmetische Funktion ist eine Funktion, die jeder positiven natürlichen Zahl einen Funktionswert aus den komplexen Zahlen zuordnet. Diese Funktionen dienen in der Zahlentheorie dazu, Eigenschaften von… … Deutsch Wikipedia
Multiplikative Funktion — Eine zahlentheoretische oder auch arithmetische Funktion ist eine Funktion, die jeder positiven natürlichen Zahl einen Funktionswert aus den komplexen Zahlen zuordnet. Diese Funktionen dienen in der Zahlentheorie dazu, Eigenschaften von… … Deutsch Wikipedia
Summatorische Funktion — Eine zahlentheoretische oder auch arithmetische Funktion ist eine Funktion, die jeder positiven natürlichen Zahl einen Funktionswert aus den komplexen Zahlen zuordnet. Diese Funktionen dienen in der Zahlentheorie dazu, Eigenschaften von… … Deutsch Wikipedia
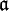 die ganzen Ideale des Zahlkörpers K durchläuft und
die ganzen Ideale des Zahlkörpers K durchläuft und 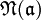 deren Absolutnorm ist. Die Reihe ζK(s) ist absolut und gleichmäßig konvergent im Bereich
deren Absolutnorm ist. Die Reihe ζK(s) ist absolut und gleichmäßig konvergent im Bereich 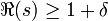 für alle δ > 0 und es gilt
für alle δ > 0 und es gilt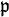 die Primideale von K durchläuft. Die Zetafunktion besitzt eine analytische Fortsetzung auf
die Primideale von K durchläuft. Die Zetafunktion besitzt eine analytische Fortsetzung auf 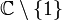 .
.