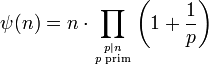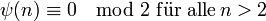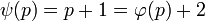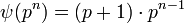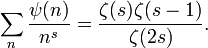Dedekindsche ψ-Funktion

Dieser Artikel wurde auf der Qualitätssicherungsseite des Portals Mathematik eingetragen. Dies geschieht, um die Qualität der Artikel aus dem Themengebiet Mathematik auf ein akzeptables Niveau zu bringen. Dabei werden Artikel gelöscht, die nicht signifikant verbessert werden können. Bitte hilf mit, die Mängel dieses Artikels zu beseitigen, und beteilige dich bitte an der Diskussion!

Die Dedekindsche ψ-Funktion (nach Richard Dedekind) ist eine mutiplikative zahlentheoretische Funktion. Sie ist nicht zu verwechseln mit anderen dedekindschen Funktionen und wird mit dem kleinen griechischen Buchstaben psi (ψ) bezeichnet. Für natürliche n ist sie definiert als

$\psi(n)=n\cdot\prod_{p|n \atop p\text{ prim}}\left(1+\frac1p\right)$

Das Produkt läuft über alle primen Teiler von n.

Werte

Nach Definition des leeren Produkts ist

ψ(1) = 1

Für die ersten natürlichen Zahlen ergeben sich die Werte 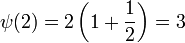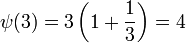$\psi(2) = 2\left(1+\frac12\right) =3$, $\psi(3) = 3\left(1+\frac13\right) =4$. Die Folge dieser Funktionswerte geht weiter mit 6, 6, 12, 24, 8, 12, 12, 18. Diese bilden die Folge A001615 in OEIS.

Eigenschaften

ψ(n) ist größer als n und gerade für alle hinreichend großen n:

$\psi(n)>n \qquad\qquad\mathrm{f\ddot ur\; alle}\, n>1$

$\psi(n)\equiv 0\mod 2\; \mathrm{f\ddot ur\; alle}\,n>2$

Für Primzahlen p gilt

$\psi(p)=p+1=\varphi(p)+2$

Dabei ist 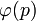$\varphi(p)$ die Eulersche Phi-Funktion, die die Anzahl der teilerfremden Zahlen angibt.

Die ψ-Funktion kann auch angegeben werden durch

$\psi(p^n) = (p+1)\cdot p^{n-1}$

für Potenzen für Primzahlen p; die Verallgemeinerung auf alle natülichen Zahlen ist dann durch die Primfaktorzerlegung und dadurch gegeben, dass 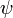$\ \psi$ eine Multiplikative Funktion ist. Mit der Riemannsche Zeta-Funktion ζ gilt dann

$\sum_n \frac{\psi(n)}{n^s} = \frac{\zeta(s) \zeta(s-1)}{\zeta(2s)}.$

Weblinks

• Eric W. Weisstein: Dedekind Function auf MathWorld (englisch)
• Die ersten 10.000 Werte der Dedekindschen psi-Funktion
• J. Chidambaraswamy: Generalized Dedekind psi functions with respect to a polynomial. II. In: Pacific J. Math. Vol. 65, Nr. 1(1976), S. 19-27.