Diedergruppen

Die n-te Diedergruppe [diˈeːdər] wird geschrieben als D_n oder D_2n.

Sie ist für 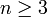$n\geq 3$ geometrisch erklärt als Symmetriegruppe der Drehungen und Spiegelungen eines regelmäßigen n-Ecks („Dieder“, d. h. „Zweiflach“). Die Gruppe D₁ besteht neben der Identität nur aus einer einzigen Spiegelung und hat somit zwei Elemente. Die Gruppe D₂ beschreibt die Symmetriegruppe eines nicht quadratischen Rechtecks oder einer Strecke (bei der zweiten Beschreibung der D₂, die geometrisch eher im Einklang mit den Fällen 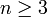$n\geq 3$ ist, lässt sich die Diedergruppe noch nicht durch ihre Wirkung auf die „beiden Ecken des Zweiecks“ treu darstellen).

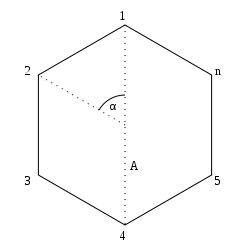
Nach Durchnummerierung der Ecken kann man die Diedergruppe für 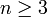$n\geq 3$ als Untergruppe der n-ten symmetrischen Gruppe S_n, also als Permutationsgruppe auffassen. Die Diedergruppe wird erzeugt von zwei Abbildungen, der Drehung um den Winkel α = 2π / n und der Spiegelung A an der Symmetrieachse durch den Punkt 1. Die einzelnen Erzeuger erzeugen je eine Untergruppe der Diedergruppe, die isomorph zu den zyklischen Gruppen C_n beziehungsweise C₂ sind. Die Ordnung der n-ten Diedergruppe ist 2n. Die Diedergruppe ist ein inneres semidirektes Produkt dieser Untergruppen.

Die durch die Permutation definierte Zahlenverknüpfung wird bei Prüfsummenverfahren als Alternative zu diversen modulo-basierten Verfahren angewendet. Die deutschen Banknoten besaßen Dieder-Prüfsummen.

Einzelnachweis

• c't 4/1997, Blütenrein. Prüfziffernverfahren auf der Basis von Diedergruppen, Seite 448, Jörg Michael [1]

Weblinks

• http://stephan-brumme.com/programming/Geldscheintester/