- Diesel-Kreisprozess
-
Der Diesel-Kreisprozess (auch Gleichdruckprozess) ist ein Vergleichsprozess für den Dieselmotor, der nach dem deutschen Ingenieur Rudolf Diesel benannt ist. Er hat gegenüber dem Ottomotor eine etwa doppelt so hohe Verdichtung und erreicht deshalb einen größeren Wirkungsgrad. Die Bezeichnung Gleichdruck beruht auf der idealisierten Annahme, dass die Wärmezufuhr bei gleichbleibendem Druck (isobar) stattfindet. Dazu im Gegensatz steht der idealisierte Otto-Prozess, bei dem die Wärmezufuhr bei konstantem Volumen erfolgt.
Inhaltsverzeichnis
Weitere Beschreibung
Um nach der hohen Verdichtung bei der Verbrennung zu hohe Temperaturen und Drücke zu vermeiden, wird durch zeitgesteuerte Einspritzung des Brennstoffes die Wärmezufuhr in den ersten Teil der Expansionsphase verlegt. Ursprünglich wurde eine Verbrennung bei konstantem Druck angestrebt, weshalb im Vergleichsprozess die Wärmezufuhr isobar verläuft. Die vier Prozessphasen sind:
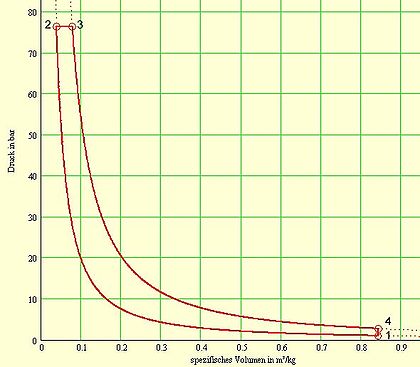
- isentrope Kompression (adiabat und reibungsfrei) (1 → 2)
- isobare Wärmezufuhr (2 → 3) (deshalb Gleichdruckprozess!)
- isentrope Expansion (3 → 4)
- isochore Wärmeabfuhr (4 → 1)
Zustandsdiagramme und Daten aus einem Berechnungsbeispiel Die vom Linienzug (1 → 2 → 3 → 4) umschlossene Fläche entspricht der spezifischen Arbeit.
Die Takte im Sinne der Bezeichnung "Viertaktmotor" stellen sich wie folgt dar:
- Ansaugen frischer Ladung: Linienzug 0 → 1
- Verdichten der Ladung: Linienzug 1 → 2
- Arbeiten (Verbrennung und Expansion): Linienzug 2 → 3 → 4
- Ausstoßen der verbrannten Ladung: Linienzug 4 → 1 → 0
Der im obigen p-v-Diagramm für den idealen Prozess (Vergleichsprozess) nicht eingezeichnete Punkt 0 befindet sich links von Punkt 1, unterhalb von Punkt 2, und entspricht dem oberen Totpunkt bei Umgebungsdruck. Beim Zweitaktmotor überlappen sich die Takte, der Punkt 0 entfällt.
Wirkungsgrad
Der Wirkungsgrad des Diesel-Prozesses ist abhängig vom geometrischen Verdichtungsverhältnis
 dem Volldruck- oder Einspritzverhältnis
dem Volldruck- oder Einspritzverhältnis  und dem Isentropenkoeffizienten
und dem Isentropenkoeffizienten 
Wir lesen aus der Abbildung die im Prozess zugeführte Wärme ab und nutzen als Arbeitsmedium Luft als ideales Gas.
-
-

- und wegen

-
-
Analog liest man für die abgeführte Wärme ab:
Für den Wirkungsgrad findet man unter Verwendung der Isentropengleichung pVκ = const:
also
Der erste Teil der Formel entspricht dem Wirkungsgrad des Gleichraumprozesses. Der zweite Teil ist der Effizienzverminderungsfaktor für den Gleichdruckprozess.
Der Gleichraumprozess hat theoretisch den besseren Wirkungsgrad als der Gleichdruckprozess!
Für die Berechnung des hier als Beispiel gezeigten Prozesses wurde üblicherweise als Arbeitsmedium Luft als ideales Gas mit konstanter spezifischer Wärmekapazität und konstantem Isentropenexponent κ gewählt. Dabei verursacht die Vernachlässigung der chemischen Umsetzung (Sauerstoff + Brennstoff → Kohlendioxid + Wasserdampf) den geringsten Fehler, weil Luft zu ca. 79 % aus Stickstoff besteht, der erhalten bleibt. Bei den auftretenden hohen Drücken verhält sich die Luft jedoch nicht mehr als ideales Gas (vergl. Realgasfaktor), und die spezifische Wärmekapazität ist bei 2000°C um ca. 30% höher als im Normzustand. Die Zustandsdiagramme und die Tabelle haben deshalb nur einen qualitativen Aussagewert.
Der reale Diesel-Motor
Die Abweichung des Gleichdruckprozesses vom realen Prozess im Diesel-Motor ist gross, weil die reale isochore Wärmezufuhr (Höchstdruck erreicht das mehrfache des Verdichtungsdruckes) nicht berücksichtigt wird. Erreichbare Wirkungsgrade im Bestpunkt liegen heute bei PKWs bei 45%, bei LKWs über 45% und bei Schiffen über 50%. Der Hauptverlust entsteht, wie beim Otto-Motor, durch die Abgaswärme und den nicht genutzten Abgasdruck. Die Kühlwasserwärme ist kleiner als die prozessbedingte Abgaswärme. Beide Wärmeströme lassen sich bei stationären Anlagen für Heizzwecke nutzen (Blockheizkraftwerk).
Literatur
- Literatur zur Technischen Thermodynamik
- Wolfgang Kalide: Kolben und Strömungsmaschinen. 1. Auflage, Carl Hanser Verlag, München Wien, 1974, ISBN 3-446-11752-0
- Jan Trommelmans: Das Auto und seine Technik. 1. Auflage, Motorbuchverlag, Stuttgart, 1992, ISBN 3-613-01288-X
- Karl-Heinz Dietsche, Thomas Jäger, Robert Bosch GmbH: Kraftfahrtechnisches Taschenbuch. 25. Auflage, Friedr. Vieweg & Sohn Verlag, Wiesbaden, 2003, ISBN 3-528-23876-3
Siehe auch
- Otto-Prozess
- Seiliger-Prozess
- Verbrennungsmotoren
- Joule-Prozess
- Clausius-Rankine-Prozess
- Carnot-Prozess
Weblinks
- TU Braunschweig - Vergleichsprozess (PDF-Datei; 42 kB)
- Universität Duisburg-Essen, Grundlagen der Technischen Thermodynamik mit Übungsaufgaben und Lösungen
Wikimedia Foundation.





![\begin{align}\eta_{Diesel}&=1+\frac{Q_{ab}}{Q_{zu}}=1+\frac{\frac{C_V}{Nk}V_1(p_1-p_4)}{\frac{C_p}{Nk}p_2V_2(\varphi-1)}\\
&=1+\frac{\varepsilon}{\kappa\cdot(\varphi-1)}\left(\frac{p_1}{p_2}-\frac{p_4}{p_3}\right)\\
&=1-\frac{\varepsilon}{\kappa\cdot(\varphi-1)}\left[\left(\frac{V_3}{V_1}\right)^{\kappa}-\left(\frac{V_2}{V_1}\right)^{\kappa}\right]\\
&=1-\frac{\varepsilon}{\kappa\cdot(\varphi-1)}\left[\left(\frac{\varphi}{\varepsilon}\right)^{\kappa}-\left(\frac{1}{\varepsilon}\right)^{\kappa}\right]\\
&=1 - \frac{1}{\kappa\cdot\varepsilon^{\kappa-1}}\cdot{\frac{{\varphi^{\kappa}-1}}{\varphi-1}}
\end{align}](0/140e004eb01dbe1e2d0a4936df9ee8e5.png)
