- Diffeomorph
-
In der Mathematik, insbesondere in den Gebieten Analysis, Differentialgeometrie und Differentialtopologie, ist ein Diffeomorphismus eine bijektive stetig differenzierbare Abbildung, deren Umkehrabbildung auch stetig differenzierbar ist.
Dabei können die Definitions- und Zielbereiche der Abbildung offene Mengen des endlichdimensionalen reellen Vektorraums
 sein oder allgemeiner differenzierbare Mannigfaltigkeiten. Je nach Differenzierbarkeitsklasse spricht man von Ck-Diffeomorphismen (
sein oder allgemeiner differenzierbare Mannigfaltigkeiten. Je nach Differenzierbarkeitsklasse spricht man von Ck-Diffeomorphismen (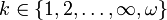 ).
).Inhaltsverzeichnis
Definition
Im Vektorraum
Eine Abbildung
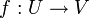 zwischen offenen Teilmengen U,V des reellen Vektorraums
zwischen offenen Teilmengen U,V des reellen Vektorraums  heißt Diffeomorphismus falls sie bijektiv ist und sowohl f als auch die Umkehrabbildung f − 1 überall stetig differenzierbar sind.
heißt Diffeomorphismus falls sie bijektiv ist und sowohl f als auch die Umkehrabbildung f − 1 überall stetig differenzierbar sind.
Sind f und f − 1 sogar k-mal stetig differenzierbar („von der Klasse Ck“,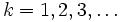 ) so nennt man f einen Ck-Diffeomorphismus. Sind f und f − 1 unendlich oft differenzierbar („von der Klasse
) so nennt man f einen Ck-Diffeomorphismus. Sind f und f − 1 unendlich oft differenzierbar („von der Klasse 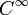 “), so bezeichnet man f als
“), so bezeichnet man f als 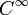 -Diffeomorphismus, sind f und f − 1 beide reell-analytisch („von der Klasse Cω“) so nennt man f einen Cω-Diffeomorphismus.
-Diffeomorphismus, sind f und f − 1 beide reell-analytisch („von der Klasse Cω“) so nennt man f einen Cω-Diffeomorphismus.Eine Abbildung
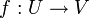 zwischen offenen Teilmengen
zwischen offenen Teilmengen 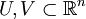 heißt lokaler Diffeomorphismus, falls jeder Punkt
heißt lokaler Diffeomorphismus, falls jeder Punkt 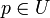 eine offene Umgebung
eine offene Umgebung 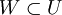 besitzt, so dass deren Bild
besitzt, so dass deren Bild 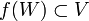 offen und die Einschränkung
offen und die Einschränkung 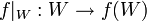 von f auf W ein Diffeomorphismus ist.
von f auf W ein Diffeomorphismus ist.Auf differenzierbaren Mannigfaltigkeiten
Auf differenzierbaren Mannigfaltigkeiten wird der Begriff genau analog definiert:
Eine Abbildung
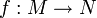 zwischen zwei differenzierbaren Mannigfaltigkeiten M und N heißt Diffeomorphismus falls sie bijektiv ist und sowohl f als auch die Umkehrabbildung stetig differenzierbar sind. Wie oben werden die Begriffe Ck-,
zwischen zwei differenzierbaren Mannigfaltigkeiten M und N heißt Diffeomorphismus falls sie bijektiv ist und sowohl f als auch die Umkehrabbildung stetig differenzierbar sind. Wie oben werden die Begriffe Ck-, 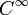 - und Cω-Diffeomorphismus und lokaler Diffeomorphismus definiert.
- und Cω-Diffeomorphismus und lokaler Diffeomorphismus definiert.Zwei Mannigfaltigkeiten M und N heißen diffeomorph, falls es einen Diffeomorphismus f von M nach N gibt. Mannigfaltigkeiten, die diffeomorph sind, unterscheiden sich bezüglich ihrer differenzierbaren Struktur nicht.
Eigenschaften
- Ein Diffeomorphismus ist immer auch ein Homöomorphismus, die Umkehrung gilt aber nicht.
- Aus der Differenzierbarkeit der Umkehrabbildung folgt, dass in jedem Punkt p die Ableitung von f (als lineare Abbildung von
 nach
nach  bzw. vom Tangentialraum TpM nach Tf(p)N) invertierbar (bijektiv, regulär, von maximalem Rang) ist.
bzw. vom Tangentialraum TpM nach Tf(p)N) invertierbar (bijektiv, regulär, von maximalem Rang) ist.
- Ist umgekehrt die Abbildung f bijektiv und (k-mal) stetig differenzierbar und ist ihre Ableitung an jeder Stelle invertierbar, so ist f ein (Ck)-Diffeomorphismus.
Eine stärkere Aussage enthält der Satz über die Umkehrabbildung:
Satz über die Umkehrabbildung
Eine differenzierbare Abbildung mit invertierbarem Differential ist lokal ein Diffeomorphismus.
Genauere Formulierung:
Sei
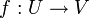 stetig differenzierbar und die Ableitung von f sei an der Stelle
stetig differenzierbar und die Ableitung von f sei an der Stelle 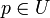 invertierbar. Dann existiert eine offene Umgebung W von p in U, so dass f(W) offen und die Einschränkung
invertierbar. Dann existiert eine offene Umgebung W von p in U, so dass f(W) offen und die Einschränkung 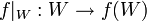 ein Diffeomorphismus ist.
ein Diffeomorphismus ist.Die Aussage gilt sowohl für Abbildungen zwischen offenen Mengen des
 als auch für Abbildungen zwischen Mannigfaltigkeiten.
als auch für Abbildungen zwischen Mannigfaltigkeiten.Beispiele
- Die Abbildung
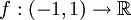 , wobei
, wobei 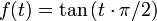 , ist ein Diffeomorphismus zwischen der offenen Menge (-1,1) und der Menge der reellen Zahlen
, ist ein Diffeomorphismus zwischen der offenen Menge (-1,1) und der Menge der reellen Zahlen  . Damit ist das offene Intervall (-1,1) diffeomorph zu
. Damit ist das offene Intervall (-1,1) diffeomorph zu  .
. - Die Abbildung
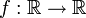 , f(x) = x3, ist bijektiv und differenzierbar. Sie ist aber kein Diffeomorphismus, denn f − 1 ist an der Stelle 0 nicht differenzierbar.
, f(x) = x3, ist bijektiv und differenzierbar. Sie ist aber kein Diffeomorphismus, denn f − 1 ist an der Stelle 0 nicht differenzierbar.
Diffeomorphie und Homöomorphie
Bei differenzierbaren Mannigfaltigkeiten in Dimension kleiner 4 impliziert Homöomorphie immer Diffeomorphie: Zwei differenzierbare Mannigfaltigkeiten der Dimension kleiner oder gleich 3, die homöomorph sind, sind auch diffeomorph. D. h., wenn es einen Homöomorphismus gibt, dann gibt es auch einen Diffeomorphismus. Dies bedeutet nicht, dass jeder Homöomorphismus ein Diffeomorphismus wäre.
In höheren Dimensionen ist dies nicht mehr unbedingt der Fall.
Ein prominentes Beispiel ist die Milnor-Sphäre, nach John Willard Milnor: Sie ist homöomorph zur normalen 7-dimensionalen Sphäre, aber nicht diffeomorph.
Literatur
- K. Jänich: Vektoranalysis, Springer Verlag, 5. Aufl., 2005, ISBN 3-5402-3741-0
- D.K. Arrowsmith, C.M. Place: An Introduction to Dynamical Systems, Cambridge University Press.
Wikimedia Foundation.

