- Dilogarithmus
-
Der Polylogarithmus ist eine spezielle Funktion, die durch die Reihe
definiert ist. Für s = 1 geht der Polylogarithmus in den gewöhnlichen Logarithmus über:
- Li1(z) = − ln(1 − z).
Im Fall s = 2 oder s = 3 spricht man entsprechend von Dilogarithmus oder Trilogarithmus. Die Definition gilt für komplexe s und z mit | z | < 1. Durch analytische Fortsetzung lässt sich diese Definition auf weitere z ausdehnen.
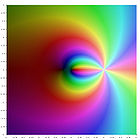
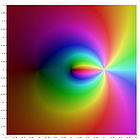
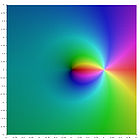
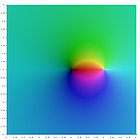
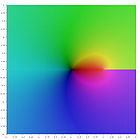
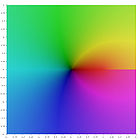
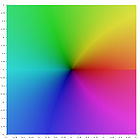
Verschiedene Polylogarithmus Funktionen in der komplexen Ebene 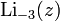
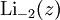
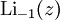
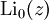
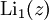
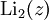
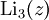
In den wichtigsten Anwendungsfällen ist s = n eine natürliche Zahl. Für diese Fälle kann man den Polylogarithmus durch die Rekursion
definieren, wonach der Dilogarithmus ein Integral des Logarithmus ist, der Trilogarithmus ein Integral des Dilogarithmus, und so fort. Für negative ganzzahlige Werte von s lässt sich der Polylogarithmus mit Hilfe rationaler Funktionen ausdrücken.
Der Polylogarithmus taucht beispielsweise im Zusammenhang mit der Fermi-Dirac-Verteilung und der Bose-Einstein-Verteilung auf.
Inhaltsverzeichnis
Funktionswerte und Rekursionen
Für ganzzahlige Werte von s gelten die folgenden expliziten Ausdrücke:
Für alle negativen ganzzahligen Werte von s kann der Polylogarithmus als Verhältnis von Polynomen in z geschrieben werden. In diesen Fällen ist er also eine rationale Funktion. Einige spezielle Ausdrücke für halbzahliges z sind im Folgenden gegeben:
ζ ist dabei die Riemannsche Zetafunktion. Für höhere Ordnungen sind keine derartigen Formeln bekannt.
Es gilt
und
mit der dirichletschen η-Funktion[1].
Ableitung
Die Ableitung der Polylogarithmen sind wieder Polylogarithmen:
Mehrdimensionale Polylogarithmen
Die mehrdimensionalen Polylogarithmen sind folgendermaßen defininert[2]:
Nielsens verallgemeinerte Polylogarithmen
Nielsen fand folgende Verallgemeinerung für den Polylogarithmus[3]:
Es gilt:
- Sn − 1,1(z) = Lin(z)
Weblinks
- Eric W. Weisstein: Dilogatrithm, Trilogarithm und Polylogarithm auf MathWorld (englisch)
- Milton Abramowitz und Irene Stegun, Handbook of Mathematical Functions, (1964) Dover Publications, New York. ISBN 978-0-486-61272-0. Abs. 27.7
- David H. Baileyb und David J. Broadhurst: A seventeenth-order polylogarithm laddera; vgl. in arxiv
Einzelnachweise
- ↑ Eric W. Weisstein: Dirichlet Eta Function auf MathWorld (englisch)
- ↑ Eric W. Weisstein: Multidimensional Polylogarithms auf MathWorld (englisch)
- ↑ Eric W. Weisstein: Nielsen Generalized Polylogarithm auf MathWorld (englisch)
Wikimedia Foundation.

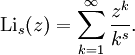
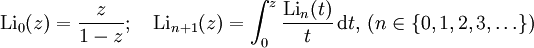
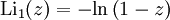
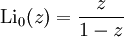
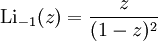
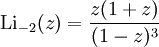
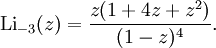
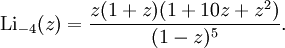
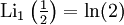
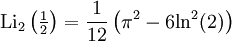
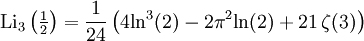
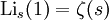
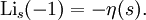
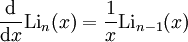
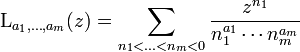
![S_{n,p}(z)=\frac{(-1)^{n+p-1}}{(n-1)!p!} \int\limits_0^1 \frac{\ln(t)^{-1}\left[\ln(1-zp)^t\right]}t \mathrm dt](/pictures/dewiki/51/304250cd30c44876784394bcf0f3cd27.png)