Dirichletsche Eta-Funktion
- Dirichletsche Eta-Funktion
-
In der Zahlentheorie ist die dirichletsche η-Funktion eine spezielle Funktion, die nach dem deutschen Mathematiker Dirichlet (1805−1859) benannt ist. Sie ist verwandt mit der riemannschen ζ-Funktion.
Sie wird mit dem kleinen griechischen Buchstaben eta (η) notiert; die dedekindsche η-Funktion, eine Modulform, wird aber ebenfalls so bezeichnet.
Definition und weitere Darstellungen
Die dirichletsche η-Funktion wird üblicherweise definiert als
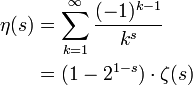
Eine Integraldarstellung enthält die Gammafunktion Γ(s) und lautet
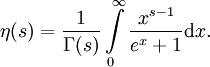
Ihre Funktionalgleichung ist
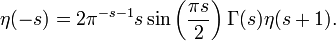
Eine Reihendarstellung ist gegeben durch
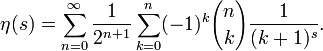
Werte
Es gilt
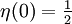
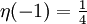
Für natürliche k gilt mit den Bernoulli-Zahlen Bk
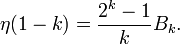
Die Werte für gerade Argumente
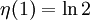 (die alternierende harmonische Reihe)
(die alternierende harmonische Reihe)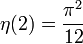
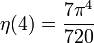
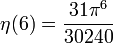
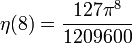
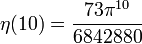
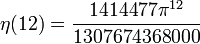
ergeben sich aus der allgemeinen Formel
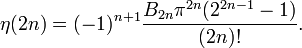
Die ersten Werte für ungerade Argumente sind
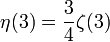
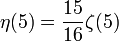
Weiteres
Die Verwandschaften von η zu der dirichletschen λ-Funktion[1] und der riemannschen ζ-Funktion werden durch folgende Formel zum Ausdruck gebracht[2]:
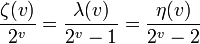
bzw.
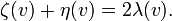
Die dirichletsche eta-Funktion ist ein Spezialfall des Polylogarithmus, denn es gilt:
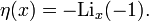
Die Ableitung ist gegeben durch
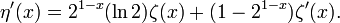
Außerdem gilt
![\int\limits_0^1\int\limits_0^1 \frac{[-\ln(x,y)]^s}{1+xy}\;\mathrm dx\,\mathrm dy=\Gamma(s+2)\eta(s+2).](/pictures/dewiki/102/fb7ce978837aae91df2c35166730c23e.png)
Literatur
Einzelnachweise
- ↑ Eric W. Weisstein: Dirichlet Lambda Function auf MathWorld (englisch)
- ↑ J. Spanier, K.B.Oldham: The Zeta Numbers and Related Functions. In: An Atlas of Functions. Washington, DC: Hemisphere, S. 25-33, 1987.
Wikimedia Foundation.
Schlagen Sie auch in anderen Wörterbüchern nach:
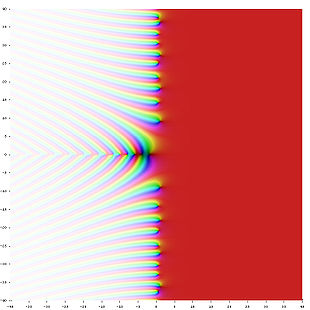
Dirichletsche η-Funktion — Die dirichletsche η Funktion in der komplexen Zahlenebene. In der analytischen Zahlentheorie ist die dirichletsche η Funktion eine spezielle Funktion, die nach dem deutschen Mathematiker Dirichlet (1805–1859) benannt ist. Sie ist verwandt mit der … Deutsch Wikipedia
Eta-Funktion — Als Eta Funktion oder η Funktion werden in der Mathematik folgende Funktionen bezeichnet: Dedekindsche η Funktion, nach dem Mathematiker Dedekind Dirichletsche Eta Funktion, nach dem Mathematiker Dirichlet Diese Seite ist eine … Deutsch Wikipedia
Dirichlet'sche Eta-Funktion — Die dirichletsche η Funktion in der komplexen Zahlenebene. In der Zahlentheorie ist die dirichletsche η Funktion eine spezielle Funktion, die nach dem deutschen Mathematiker Dirichlet (1805−1859) benannt ist. Sie ist verwandt mit der … Deutsch Wikipedia
ETA — ist: ein weiblicher Vorname Eta (Majuskel Η, Minuskel η) der 7. Buchstabe des griechischen Alphabets eine alte Bezeichnung für einen bestimmten Teil der Buraku, einer japanische Minderheitengruppe ein griechischer Buchstabe, der in der Technik… … Deutsch Wikipedia
Eta — Aussprache antik [ɛː] modern [i] Entsprechungen lateinisch H kyrillisch И h … Deutsch Wikipedia
Dirichlet'sche η-Funktion — Die dirichletsche η Funktion in der komplexen Zahlenebene. In der Zahlentheorie ist die dirichletsche η Funktion eine spezielle Funktion, die nach dem deutschen Mathematiker Dirichlet (1805−1859) benannt ist. Sie ist verwandt mit der … Deutsch Wikipedia
Heta/eta — Eta Aussprache antik [ɛː] modern [i] Entsprechungen lateinisch H … Deutsch Wikipedia
Spezielle Funktion — In der Analysis, einem Teilgebiet der Mathematik, bezeichnet man gewisse Funktionen als spezielle Funktionen, weil sie sowohl in der Mathematik selbst als auch in ihren Anwendungen (z. B. in der mathematischen Physik) eine tragende Rolle… … Deutsch Wikipedia
Zeta-Funktion — Ursprünglich war mit Zeta Funktion oder ζ Funktion in der Mathematik die komplexe Funktion gemeint. Heute heißt diese genauer Riemannsche Zeta Funktion, zu Ehren von Bernhard Riemann, der um 1850 bedeutende Arbeiten zur Untersuchung dieser… … Deutsch Wikipedia
Riemannsche ζ-Funktion — Die riemannsche Zeta Funktion in der komplexen Ebene Die in obigem Bild verwendete Kolo … Deutsch Wikipedia
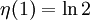 (die alternierende harmonische Reihe)
(die alternierende harmonische Reihe)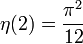
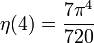
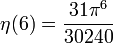
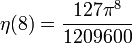
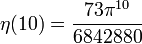
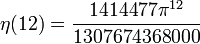

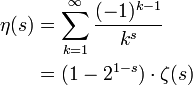
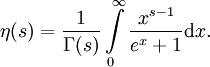
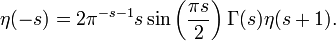
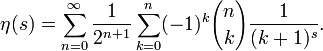
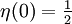
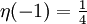
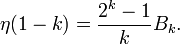
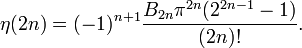
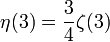
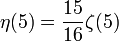
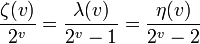
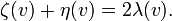
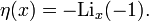
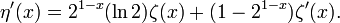
![\int\limits_0^1\int\limits_0^1 \frac{[-\ln(x,y)]^s}{1+xy}\;\mathrm dx\,\mathrm dy=\Gamma(s+2)\eta(s+2).](/pictures/dewiki/102/fb7ce978837aae91df2c35166730c23e.png)