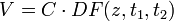Diskontfaktor

Die Artikel Diskontierungsfaktor und Abzinsung überschneiden sich thematisch. Hilf mit, die Artikel besser voneinander abzugrenzen oder zu vereinigen. Beteilige dich dazu an der Diskussion über diese Überschneidungen. Bitte entferne diesen Baustein erst nach vollständiger Abarbeitung der Redundanz. Marinebanker 22:45, 3. Mai 2009 (CEST)

Abzinsung zur Ermittlung des Kapitalwerts (Beispielhafte Übersicht)

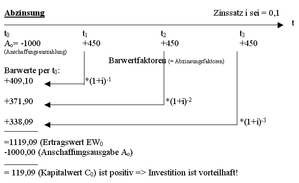
Die Abzinsung (auch Diskontierung, engl. discounting; oft fälschlich auch Abdiskontierung genannt) ist eine Rechenoperation aus der Finanzmathematik, bei der Wert einer zukünftigen Zahlung für einen Zeitpunkt, der vor dem der Zahlung liegt, berechnet wird. Häufig, aber nicht notwendigerweise wird mittels Diskontierung der gegenwärtige Wert (Barwert) einer zukünftigen Zahlung ermittelt.

Auf Grund der Existenz von Zinsen hat derselbe Geldbetrag einen um so höheren Wert, je früher man ihn erhält. Dieser Zusammenhang wird durch die Rechenoperation der Abzinsung wiedergegeben.

Der Wert V, den eine zum Zeitpunkt t₂ fließende Zahlung der Höhe C zum Zeitpunkt t₁ hat, berechnet sich als Produkt von C und dem Diskontierungsfaktor oder Abzinsfaktor DF, der eine Funktion der Zeitpunkte t₁ und t₂ sowie des maßgeblichen Zinssatzes z ist.

$V = C \cdot DF(z,t_1,t_2)$

Da es sich um eine Abzinsung handelt, liegt der Zeitpunkt t₁ vor dem Zeitpunkt t₂ (t₁ < t₂). Positive Zinssätze vorausgesetzt, ist der Diskontierungsfaktor DF immer kleiner als 1 und größer als 0. Die genaue Form des Diskontierungsfaktors hängt von der gewählten Zinskonvention ab.

Bei den Zinsen kann es sich sowohl um tatsächliche Zinsen (Marktzinsen) als auch um fiktive, etwa kalkulatorische oder Alternativzinsen handeln (wie zum Beispiel bei der Unternehmensbewertung).

Bestimmung des Diskontierungsfaktors

Im Folgenden wird die Form des Diskontierungsfaktors zunächst für eine Abzinsung auf die Gegenwart (d. h. t₁ = 0) angegeben. Der Diskontierungsfaktor hängt dann nur noch vom Zeitpunkt der künftigen Zahlung t₂ = t und dem verwendeten Zinssatz z ab.

Lineare Verzinsung

Die lineare Verzinsung wird normalerweise für Zeiträume angewendet, die kleiner als ein Jahr sind. Der Diskontierungsfaktor DF berechnet sich zu

$DF = \frac{1}{1 + \frac{n}{m}z}$,

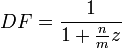wobei n die Anzahl der Zinstage bis t₂ und M die Anzahl der Zinstage pro Jahr nach der gewählten day count convention sind.

• Beispiel

Beträgt der Zinssatz 5% und t₂ liegt 3 Monate in der Zukunft, dann beträgt der Diskontierungsfaktor bei einer Zinsberechnungsmethode von 30/360 (d. h. 30 Zinstage pro Monat und 360 Zinstage pro Jahr, sog, deutsche Methode)

$DF = \frac{1}{(1 + \frac{3 \cdot 30}{360}\cdot0,05)} = \frac{1}{(1,0125)} = 0,98765$.

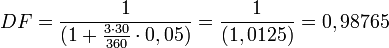Das heißt, dass eine Zahlung von 100 EUR, die man in 3 Monaten erhält, abgezinst einen gegenwärtigen Wert von 98,77 EUR hätte.

Exponentielle Verzinsung

Die exponentielle Verzinsung wird normalerweise für Zeiträume verwendet, die länger als ein Jahr sind. Sie berücksichtigt implizit Zinseszinseffekte. Liegt der Zinssatz bei z und erfolgt die Zahlung in t₂ Jahren, so ist der Diskontierungsfaktor

$DF = \frac{1}{(1 + z)^{t_2}}$.

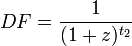• Beispiel

Beträgt der Zinssatz wiederum 5% und t₂ liegt 4 Jahre in der Zukunft, dann beträgt der Diskontierungsfaktor

$DF = \frac{1}{(1 + 0,05)^4} = 0,82270$.

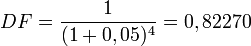Stetige Verzinsung

Die stetige Verzinsung ist ein Sonderfall der exponentiellen Verzinsung und wird häufig bei theoretischen finanzmathematischen Fragestellungen verwendet. Auch sie berücksichtigt implizit Zinseszinseffekte. Der Diskontierungsfaktor für eine Zahlung in t₂ Jahren lautet hier

$DF = e^{-z \cdot t_2}$.

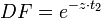e ist hier bei die Eulersche Konstante

• Beispiel

Bei Verwendung derselben Parameter wie bei dem Beispiel zur exponentiellen Verzinsung beträgt der Diskontierungsfaktor

$DF = e^{-0,05 \cdot 4} = 2,71818^{-0,2} = 0,81873$,

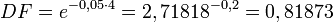liegt also nahe bei dem für die exponentielle Verzinsung

Abzinsung auf einen zukünftigen Zeitpunkt

Liegt der Zeitpunkt, auf den abgezinst werden soll, in der Zukunft, erfolgt die Berechnung analog. Der zu verwendende Zinssatz ist dann ein Zinssatz für einen Zeitraum, der in der Zukunft startet und entspricht damit einem Forward-Zins. Wird ein Zinssatz von z angenommen, der Zeitpunkt der Zahlung t₂ liegt in 9 Monaten und es soll auf einen Zeitpunkt t₁ in 3 Monaten abgezinst werden, so lautet der Diskontfaktor

$DF = \frac{1}{1 + \frac{(9-3)\cdot30}{360}z}$,

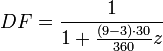wenn eine lineare Verzinsung und wiederum die deutsche Zinsmethode angenommen wird. Es wird über 9-3 = 6 Monate abgezinst, weil der Zeitpunkt, auf den abgezinst wird, 6 Monate vor dem Zeitpunkt der Zahlung liegt.

Siehe auch

• Zinseszinsrechnung
• Investitionsrechnung