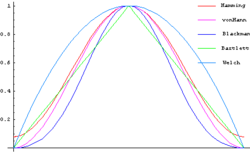
- Dreieck-Fenster
-
Der Begriff Fensterfunktion stammt aus der digitalen Signalverarbeitung. Die Fensterfunktion legt fest, mit welcher Gewichtung die bei der Abtastung eines Signals gewonnenen Abtastwerte innerhalb eines Ausschnittes (Fenster) in nachfolgende Berechnungen eingehen. Fensterfunktionen kommen bei der Frequenzanalyse (z. B. mittels diskreter Fouriertransformation), beim Filterdesign, beim Beamforming und anderen Signalverarbeitungsanwendungen zum Einsatz.
Inhaltsverzeichnis
Anwendungen
Frequenzanalyse
Ein andauerndes Signal wird in der Regel in Blöcken verarbeitet. Da Blocklängen in der Praxis endlich sind, kommt es zum sogenannten Leck-Effekt (Leakage Effect), wenn die Blocklänge nicht gerade ein Vielfaches der Periode des Signals ist. Das errechnete Frequenzspektrum wird zu breit, es ist bildlich gesprochen „verschmiert“. Dieser Effekt resultiert aus den Eigenschaften der Fourier-Transformation (Multiplikation von Signalen führt zu Faltung im Frequenzraum).
Durch die Verwendung einer geeigneten Fensterfunktion lässt sich der Effekt vermindern, aber nicht ganz vermeiden. Das Signal wird hierbei meistens am Fensterbeginn „eingeblendet“ und am Fensterende „ausgeblendet“, was zu einer künstlichen Periodisierung des Signals innerhalb der Zeitfensterlänge führt.
Die Fensterfunktion beeinflusst neben der spektralen Verbreiterung außerdem die Frequenzselektivität und den maximal möglichen spektralen Fehler. Es gibt verschiedene Fensterfunktionen unterschiedlicher Komplexität. Die Auswahl einer passenden Fensterfunktion ist daher stets ein Kompromiss, der den speziellen Anforderungen des jeweiligen Anwendungsfalls Rechnung trägt.
Filterdesign
Eine häufig angewandte Methode für das Design von digitalen Filtern mit endlicher Impulsantwort (FIR-Filter) ist die Fenstermethode (Window method).
Dabei wird der gewünschte Frequenzgang des Filters definiert und mit der inversen Fouriertransformation die ideale Impulsantwort ermittelt. Das Resultat der inversen Fouriertransformation ist in der Regel unendlich lang. Um eine endlich lange Impulsantwort mit der gewünschten Filterlänge N zu erhalten, wird durch eine Fensterfunktion ein Ausschnitt der unendlichen Impulsantwort ausgewählt. Der tatsächliche Frequenzgang des Filters entspricht somit der Faltung des gewünschten Frequenzgangs mit der Fouriertransformierten der Fensterfunktion.
Im Filterdesign führen breite (selektive) Fensterfunktionen zu steilen Übergängen zwischen Durchlass- und Sperrbereich, aber zu geringer Sperrdämpfung. Schmale (nicht selektive) Fensterfunktionen führen zu flachen Übergängen zwischen Durchlass- und Sperrbereich, dafür aber zu großer Sperrdämpfung.
Beispiele von Fensterfunktionen
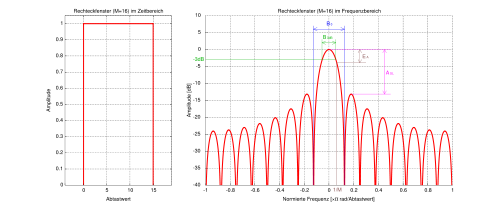
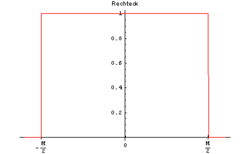
Rechteck-Fenster
Die Rechteck-Fensterfunktion ist im gesamten Fensterbereich 1 und außerhalb 0. Die naive Verarbeitung des Eingangssignals in Blöcken entspricht der Anwendung dieser Fensterfunktion.
Auswirkung
Für eine Kosinus-Funktion f(x) = cos(2πf0x) würde man im durch Fouriertransformtion berechneten Spektrum erwarten, dass lediglich bei der Frequenz f0 bzw. − f0 die Amplitude
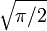 aufgetragen ist.
aufgetragen ist.Allgemein entspricht aber eine Multiplikation im Ausgangsraum einer Faltung der Transformierten im Fourierraum (Spektrum). Die Transformierte des Rechteckfensters ist die sinc-Funktion
Das tatsächlich resultierende Spektrum entspricht also einer Faltung der sinc-Funktion mit dem erwarteten Spektrum.
Nur für eine Fensterbreite
erhält man das erwartete Spektrum, denn in diesem Fall entspricht eine Blocklänge genau einer Periode des Eingangssignals; eine periodische Fortsetzung der mit dem Rechteckfenster multiplizierten Funktion führt wieder zur Ursprungsfunktion.
Siehe auch: Leckeffekt
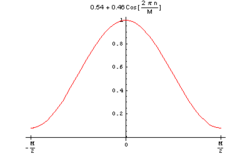
Hamming-Fenster
Funktion:
dabei ist M die Fensterbreite und n der aktuelle Index des Eingangssignals. (Wie auch im Folgenden wird M als gerade angenommen.) Diese Fensterfunktion ist benannt nach Richard Hamming.
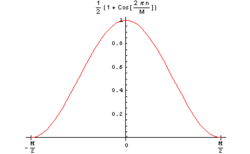
von-Hann-Fenster (auch bekannt als „Raised-Cosinus-Fenster“)
Funktion:
dabei ist M die Fensterbreite und n der aktuelle Index des Eingangssignals.
Die Bezeichnung Hann-Fenster stammt aus der Publikation „Particular Pairs of Windows.“ von R. B. Blackman und John W. Tukey (veröffentlicht in „The Measurement of Power Spectra, From the Point of View of Communications Engineering“, New York: Dover, 1959, pp. 98-99), die dieses nach Julius von Hann benannt haben. Aus diesem Artikel stammt auch die weit verbreitete Bezeichnung Hanning-Fenster, wobei dort jedoch lediglich die Anwendung des Hann-Fensters als „hanning“ (abgeleitet von „to hann“) bezeichnet wird.
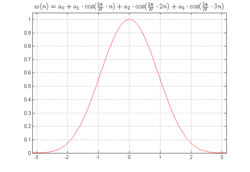
Blackman-Fenster (3-Term)
dabei ist M die Fensterbreite und n der aktuelle Wert des Eingangssignals.
Blackman-Harris Fenster (4-Term)
Funktion:
mit den Koeffizienten a0 = 0,35875, a1 = 0,48829, a2 = 0,14128 und a3 = 0,01168. Die Fensterlänge beträgt M.
F. J. Harris veröffentlichte diese Funktion als Abwandlung der Blackman-Fensterfunktion.[1]
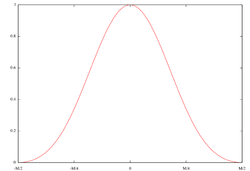
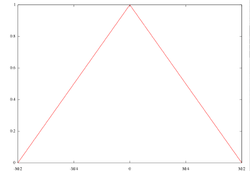
Bartlett-Fenster
Die Dreieckfunktion:
dabei ist M die Fensterbreite und n der aktuelle Wert des Eingangssignals.
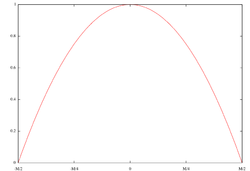
Welch-Fenster
Funktion:
dabei ist M die Fensterbreite und n der aktuelle Wert des Eingangssignals.
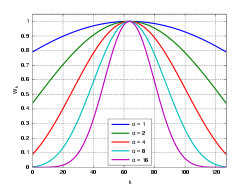
Kaiser-Fenster
Das Fenster ist definiert durch die Funktion[2]:
Dabei ist I0 die modifizierte Besselfunktion nullter Ordnung. Die Fensterbreite beträgt M und α ist ein reeller Faktor, welcher die Form des Fensters bestimmt. Je größer α, desto schmaler wird das Fenster und α = 0 entspricht einem Rechteckfenster.
Die Fouriertransformierte des Fensters w(n) ist definiert durch die
Funktion
für die normierte Frequenz
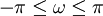 .
.Mit der Funktion WK(ω) lässt sich die Breite des Hauptmaximums
und die relative Dämpfung des Nebenmaximums
berechnen. Daraus ergibt sich: Wenn α größer wird, nimmt die Breite des Hauptmaximums zu und die relative Amplitude des Nebenmaximums ab.
Weitere
Dolph-Chebyshev[3], Rife-Vincent[4], Slepian (DPSS), Poisson
Vergleich der Fensterfunktionen
Bewertungskriterien für Fensterfunktionen
Alle gängigen Bewertungskriterien beziehen sich auf die Übertragungsfunktion (Fouriertransformation der Fensterfunktion) im Frequenzbereich. Zum Vergleich und zur Auswahl der richtigen Fensterfunktion werden die folgenden Bewertungskriterien verwendet:
Breite des Hauptmaximums (Hauptzipfels)
Eine Verbreiterung des Hauptmaximums führt zu einem schnelleren Abfall der Nebenmaxima (Nebenzipfel), erhöht die Dynamik der Fensterfunktion und verringert den Leck-Effekt. Allerdings wird dabei die Frequenzselektivität verringert. Fensterfunktionen mit breitem Hauptmaximum werden deshalb auch als nichtselektive, dynamische Fenster bezeichnet, und solche mit schmalem Hauptmaximum als selektive, nichtdynamische Fenster.
Die Breite des Hauptmaximums wird meistens als 3-dB-Grenzfrequenz angegeben. Dies ist die Frequenz, bei der die Amplitude des Hauptmaximums um 3 dB abgefallen ist. Selten wird auch die gesamte Breite des Maximums bis zu den Nullstellen angegeben.
Relative Amplitude des Nebenmaximums
Starke Nebenmaxima einer Fensterfunktion erhöhen den Leck-Effekt bei der Frequenzanalyse und deuten auf eine geringe Dynamik der Fensterfunktion hin.
Als Bewertungskriterium wird das Verhältnis zwischen der Amplitude des Hauptmaximums und der Amplitude des höchsten Nebenmaximums verwendet.
Leck-Faktor (Leakage Factor)
Der Leck-Effekt wird durch tiefe Nebenmaxima verringert. Der Leck-Faktor ist definiert als das Verhältnis der Leistung unter allen Nebenmaxima zur Leistung der gesamten Funktion.
Maximaler Abtastfehler
Der maximale Abtastfehler ist definiert als das Verhältnis der Amplitude des Hauptmaximums zur Amplitude bei der Frequenz π/Fensterlänge.
Vergleich nach oben genannten Bewertungskriterien
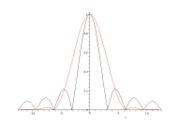
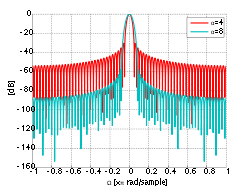
Verbreiterung des Hauptmaximums führt zu schnellerem Abfall der Nebenmaxima. Exemplarisch ist dies in nebenstehender Abbildung an Rechteck- und Hamming-Fenster gezeigt.
Fensterbezeichnung rel. Amplitude des Nebenmaximums Breite des Hauptmaximums max. Abtastfehler Rechteck - 13 dB 4 π / (M+1) 3,92 dB Dreieck (Bartlett) - 25 dB 8 π / M 1,82 dB von Hann - 31 dB 8 π / M 1,42 dB Hamming - 41 dB 8 π / M 1,78 dB Kaiser-Bessel (α=2) - 46 dB 1,46 dB Kaiser-Bessel (α=3,5) - 82 dB 0,89 dB Blackman - 57 dB 12 π / M 1,10 dB Siehe auch
Einzelnachweise
- ↑ Frederic J. Harris, On the use of Windows for Harmonic Analysis with the Discrete Fourier Transform, Proceedings of the IEEE, Vol. 66, No. 1, January 1978, pp 51-83.
- ↑ James F. Kaiser and Ronald W. Schafer, On the Use of the Io-Sinh Window for Spectrum Analysis, IEEE Transactions on Acoustics, Speech and Signal Processing, Vol. ASSP-28, No. 1, February 1980, pp 105-107.
- ↑ F. J. Harris, ``On the use of windows for harmonic analysis with the discrete Fourier transform, Proceedings of the IEEE, vol. 66, pp. 51-83, Jan 1978.
- ↑ D. C. Rife and G. A. Vincent, "Use of the Discrete Fourier Transform in the Measurement of Frequencies and Levels of Tones," Bell Sys. Tech. J., pp. 197ff (1970 Feb.).
Literatur
- Karl-Dirk Kammeyer, Kristian Kroschel: Digitale Signalverarbeitung. 6 Auflage. Teubner, 2006, ISBN 3-8351-0072-6.
Wikimedia Foundation.

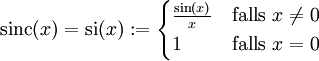
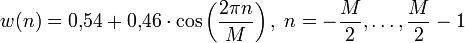
![w(n) = \frac{1}{2}\left[1 + \cos\left(\frac{2\pi n}{M}\right)\right],](/pictures/dewiki/55/76b65e3abfa6ef82f4f2b293f314b96b.png)
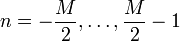
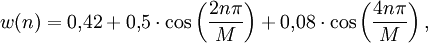
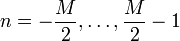
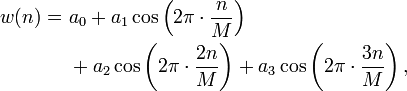
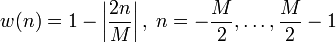
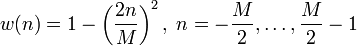
![w(n) = \frac{I_0\left(\alpha\left[1 - \left(\frac{2n}{M}\right)^2\right]^\frac{1}{2}\right)}{I_0\left(\alpha\right)}, \; n = -\frac{M}{2}, \ldots, \frac{M}{2} - 1](/pictures/dewiki/56/81f04b486a7f8d0ad7a0c352428f4419.png)
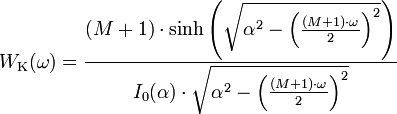
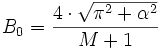
![A_\mathrm{SL} = 20\cdot\log_{10}\left[\frac{\sinh\alpha}{0{,}217234\alpha}\right]](/pictures/dewiki/54/60be6c2ff58514a397ea681b87b994dd.png)