Leck-Effekt

Der Leck-Effekt, Lattenzaun-Effekt oder Leakage-Effekt ist ein Phänomen der Signalanalyse. Er bewirkt durch den endlich langen Beobachtungszeitraum im Rahmen von Spektralanalysen, wie der Fourieranalyse, dass sich in den daraus berechneten Frequenzspektrum auch Frequenzanteile finden, welche bei einem theoretisch unendlich langen Beobachtungszeitraum des Ursprungsignals nicht vorkommen. Dieser Effekt des „Lecken“ oder „Verschmieren“ im Frequenzspektrum wird im Englischen als leakage bezeichnet.

Allgemeines

Spektrale Darstellung des Leck-Effektes durch die in zweiter Zeile erfolgte zeitliche Limitierung der Sinusschwingung

Der Leck-Effekt lässt sich bei der zeitkontinuierlichen Signalanalyse grundsätzlich nicht vermeiden, da in Realität jedes Signal einen zeitlichen Beginn und Ende aufweisen muss und zeitlich nicht unendlich lange periodisch fortgesetzt werden kann. Es lassen sich durch geeignete Methoden wie entsprechend lang gewählte Beobachtungszeiträume oder die Verwendung spezieller Filter basierend auf Fensterfunktionen, die Auswirkungen des Leck-Effektes minimieren. Auch bei zeitdiskreten Signalen und deren Analyse, wie beispielsweise im Rahmen der diskreten Fourier-Transformation, tritt der Leck-Effekt auf, kann aber in diesem Fall in ganz bestimmten Situationen zufolge der periodischen Fortsetzung im diskreten Spektrum als Sonderfall gänzlich vermieden werden.

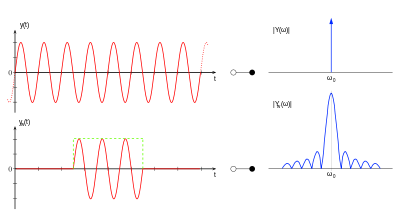
Ohne zeitlicher Limitierung, dieser theoretische Fall einer unendlich lang dauernden Sinusschwingung wie in der Abbildung im oberen Fall angedeutet, resultiert bei der Berechnung des Betragsspektrum im Rahmen der Fouriertransformation im Bereich positiver Frequenzen zu einem Dirac-Impuls bei der Kreisfrequenz ω₀. Die unendlich lange Sinusschwingung stellt ein sogenanntes Leistungssignal dar. Wird die Sinusschwingung wie in der Abbildung darunter dargestellt zu einem bestimmten Zeitpunkt eingeschalten und danach ausgeschalten, dieser Zeitbereich wird auch als „Beobachtungsintervall“ bezeichnet, kommt es zu einem „Verschmieren“ des Dirac-Impuls im Spektrum welcher als Leck-Effekt bezeichnet wird. Die endlich lange Sinusschwingung geht durch die Anwendung einer Rechteckfunktion als Fensterfunktion in ein Energiesignal über. Die rechteckförmige Fensterfunktion ist in der Abbildung bei y_w(t) als grün-strichlicherte Linie dargestellt.

Mathematisch stellt diese zeitliche Limitierung mit der Fensterfunktion von Zeitsignalen eine Multiplikation dar, welche bis zu Beginn des Zeitfensters 0, während der Zeitfensterdauer 1 und ab dem Ende des Zeitfensters wieder 0 ist. Dies führt im Frequenzbereich zu einer Faltung des Signalspektrums mit dem Spektrum der Rechteckfunktion welche durch die si-Funktion beschrieben wird. Das Betragsspektrum ist symmetrisch um die Kreisfrequenz ω₀.

Durch von der Rechteckfunktion abweichende Fensterfunktionen mit denen das Zeitsignal im Zeitbereich multipliziert wird, können diese Auswirkungen vermindert, jedoch nicht gänzlich vermieden werden. Dabei wird das Ansteigen bzw. Abfallen der Amplitude langsamer als wie bei der Rechteckfunktion vergenommen, so dass das Spektrum der Fensterfunktion möglichst um ω₀ konzentriert ist und an den Rändern der Fensterfunktion möglichst viele Ableitungen gegen 0 gehen. Eine gebräuchliche Fensterfunktionen mit geringen Leckeffekt ist das Hanning-Fenster. Zu Beachten ist, dass zur Reduzierung des Leck-Effektes die Filterfunktion im Zeitbereich, und nicht wie sonst bei Filtern üblich im Spektralbereich, angewendet wird.

Zeitdiskrete Systeme

Leck-Effekt bei zeitdiskreten Systemen

In zeitdiskreten Systemen, wie im Rahmen der digitalen Signalverarbeitung, tritt, bis auf einen Sonderfall, bei der Diskreten Fourier-Transformation (DFT) und den darauf aufgebauten optimierten Varianten der Schnellen Fourier-Transformation (FFT) ein Leck-Effekt zufolge der Blockbildung und damit verbundenen zyklischen Faltung auf. Dabei werden im Zeitbereich eine bestimmte, endliche Anzahl von diskreten Abtastwerten genommen und aufgrund dieser Werte das diskrete Spektrum berechnet. Aufgrund des diskreten Spektrums kommt es im Zeitbereich zu einer periodischen Fortsetzung der zeitlich beschränkten Abtastwerte.

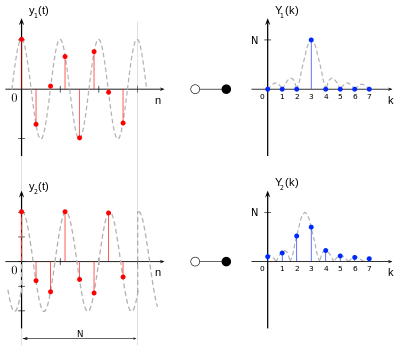
Dieser Umstand kann in dem Sonderfall einer harmonischen Schwingung, deren Periodendauer ein ganzzahliges Vielfaches des Beobachtungsfensters beträgt, d.h. die periodische Fortsetzung entspricht genau dem Signalverlauf ausserhalb des Beobachtungsintervalls, ausgenutzt werden da es in diesem Fall zu keinem Leck-Effekt kommt. Dieser Fall ist in nebenstehender Abbildung im oberen Bereich dargestellt. Das Beobachtungsintervall umfasst dabei exakt drei Perioden der harmonischen Signalfrequenz, grau-strichliert hinterlegt dargestellt, welche mit N = 8 Abtastwerten (rote Punkte) abgetastet wird. Der rechts dargestellte Betragsverlauf des diskreten Spektrums mit der Kreiswellenzahl k der DFT liefert nur eine Spektralkomponente mit einem Wert ungleich 0 bei k = 3 mit dem Wert N = 8. Die einzelnen Spektralkomponenten werden in diesem Zusammenhang auch als Bins bezeichnet. Durch die zeitlich beschränkte Abtastung zufolge der Blockbildung, dies entspricht einer überlagerten Rechteckfunktion im Zeitbereich, tritt im Spektrum die grau-strichlierte und hinterlegte si-Funktion auf. An den Nullstellen dieser si-Funktion liegen alle restlichen Bins ausserhalb der Signalfrequenz. Dieser Sonderfall ist nur dann stabil zu erreichen und zu halten, wenn die Abtastfrequenz mit der Signalfrequenz synchronisiert ist.

Beträgt die Periodendauer kein ganzzahliges Vielfaches des Beobachtungsfensters, dieser Fall ist darunter abgebildet, kommt es zu einem Leck-Effekt: Das diskrete Spektrum wird über mehrere Bins gespreitzt. Das Maximum ist im diskreten Spektrum in diesem Fall nicht direkt darstellbar, die Anteile werden quasi auf benachbarte Bins „verteilt“. Dieser Fall tritt auch bei allgemeinen Signalverläufen auf, welche beispielsweise aus einer beliebigen Summe verschiedener harmonischer Schwingungen gebildet werden.

Zur Reduzierung des Leck-Effektes werden bei zeitdiskreten Systemen zeitdiskrete Fensterfunktionen eingesetzt und die abgetastete Signalfolge im Zeitbereich zunächst der Folge der Fensterfunktion unterworfen, wie beispielsweise einer diskreten Hanning-Fensterfunktion, und anschliessend die Diskrete Fourier-Transformation ausgeführt.

Literatur

• Fernando Puente León, Uwe Kiencke, Holger Jäkel: Signale und Systeme. 5. Auflage. Oldenbourg, 2011, ISBN 978-3-486-59748-6.