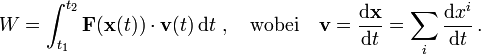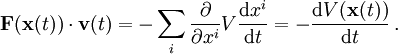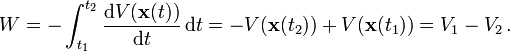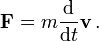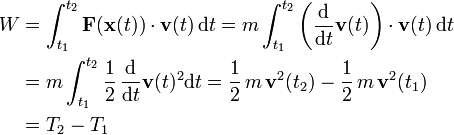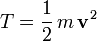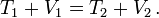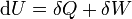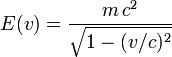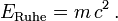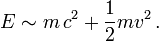Energiesatz

Der Energieerhaltungssatz sagt aus, dass die Gesamtenergie eines abgeschlossenen Systems sich nicht mit der Zeit ändert. Zwar kann Energie zwischen verschiedenen Energieformen umgewandelt werden, beispielsweise von Bewegungsenergie in Wärme. Es ist jedoch nicht möglich, innerhalb eines abgeschlossenen Systems Energie zu erzeugen oder zu vernichten: Die Energie ist eine Erhaltungsgröße.

Die Gesamtenergie in einem abgeschlossenen System bleibt konstant.

Unter einem abgeschlossenen System versteht man ein System ohne Energie-, Informations- oder Stoffaustausch und ohne Wechselwirkung mit der Umgebung.

Der Energieerhaltungssatz lässt mit Hilfe des Noethertheorems daraus ableiten, dass die für das System gültigen Gesetze der Physik nicht von der Zeit abhängen.

Umgangssprachliche Aspekte

Oftmals wird irrtümlich die Umwandlung von Energieformen mit dem Verlust von Energie identifiziert. Man spricht in diesem Zusammenhang beispielsweise von Energieverbrauch, Energieverschwendung, Energiesparen und Energieverlust. Meist meint man damit den Verlust von technisch leicht nutzbaren Energieformen und damit Phänomene und Probleme, die durch die Entropie bedingt sind. Jene Energiebegriffe sind im physikalischen Sinn aber nicht richtig, da beispielsweise ein Kraftfahrzeug keine Energie verbraucht beziehungsweise vernichtet, sondern lediglich chemische Energie in kinetische Energie und thermische Energie umwandelt. Energie kann nicht aus dem Nichts entstehen und auch nicht in dieses verschwinden. Verschiedene Energieformen, also beispielsweise kinetische Energie, thermische Energie, Strahlungsenergie, Bindungsenergie usw. wandeln sich lediglich ineinander um, sind anschließend allerdings technisch meist deutlich schwieriger weiterzunutzen (siehe hierzu auch Wirkungsgrad).

Geschichte

Als erster hat der Arzt Julius Robert von Mayer (1814-1878) den Energieerhaltungssatz formuliert. Er hat 1842 durch Versuche den Wert des mechanischen Wärmeäquivalents festgestellt und so nachgewiesen, dass sich Bewegungsenergie vollständig in Wärme umwandeln lässt. Unabhängig von Mayer tat dies auch 1843 James Prescott Joule, dessen Arbeiten damals weit bekannter waren. Endgültig ausformuliert wurde der Energieerhaltungssatz 1847 von Hermann von Helmholtz.

Auch der Energieerhaltungssatz ist in der Geschichte der Physik nicht immer unumstritten gewesen. Das berühmteste Beispiel ist Niels Bohr, der bei mehreren Gelegenheiten nur eine statistische (gemittelte) Erhaltung der Energie bei Quantenprozessen befürwortete. Zuerst 1924 in der sogenannten BKS-Theorie mit John C. Slater und Hendrik Anthony Kramers^[1], bei der es darum ging die ältere Quantentheorie in Wechselwirkung mit einem klassischen elektromagnetischen Feld in Einklang zu bringen, wobei Bohr insbesondere gegen die Idee des Teilchencharakters der Strahlung (Photon-Konzept von Albert Einstein, damals kurz zuvor im Compton-Effekt experimentell bestätigt) opponierte. Nur wenig später wurde diese Theorie durch Experimente von Arthur Holly Compton selbst, aber auch Hans Geiger und Walther Bothe widerlegt und die Gültigkeit des Energieerhaltungssatzes auch auf Quantenebene bestätigt. Auch bei späterer Gelegenheit versuchte Bohr eine nur statistische Gültigkeit des Energieerhaltungssatzes zur Erklärung zunächst rätselhafter quantenmechanischer Phänomene zu verwenden, so beim Betazerfall, wo die fehlende Energie der Zerfallsprodukte aber kurz darauf durch das Postulat eines neuen, nur schwach wechselwirkenden Teilchens, des Neutrinos, durch Wolfgang Pauli erklärt wurde.

Heute gilt der Energieerhaltungssatz bei der überwiegenden Mehrzahl der Physiker als etabliert und wird sogar häufig zur Definition der Energie herangezogen.

Energieerhaltungssatz in der Newtonschen Mechanik

Zwei beliebige Wege in einem konservativen Kraftfeld.

Bei Bewegung von Teilchen in einem konservativen Kraftfeld ist die Summe von kinetischer Energie T und potentieller Energie V, die Gesamtenergie E = T + V, erhalten. Dabei ist die Kraft der negative Gradient des Potentials

$\mathbf{F} = - \nabla V$.

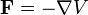Bewegt sich ein Teilchen mit der Zeit t in solch einem Kraftfeld auf beliebigen Wegen 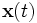$\mathbf x(t)$ von einem Startpunkt zu einem Ziel, so ist für die Arbeit, die dabei am Teilchen verrichtet wird, der Weg unerheblich. Unabhängig vom Weg ist die geleistete Arbeit die Differenz der potentiellen Energien an Start und Ziel.

Die Arbeit W ist definiert als das Zeitintegral über die Kraft F mal der Geschwindigkeit v

$W = \int_{t_1}^{t_2} \mathbf F(\mathbf x(t)) \cdot \mathbf v(t) \, \mathrm dt\ ,\quad \text{wobei} \quad \mathbf v = \frac{\mathrm d \mathbf x}{\mathrm d t}=\sum_i \frac{\mathrm d x^i}{\mathrm d t}\,.$

Der Integrand ist die negative Zeitableitung der potentiellen Energie 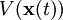$V(\mathbf{x}(t))$, denn

$\mathbf F(\mathbf x(t)) \cdot \mathbf v(t) = -\sum_i \frac{\partial}{\partial x^i}V \frac{\mathrm d x^i}{\mathrm d t}= - \frac{\mathrm dV(\mathbf x(t))}{\mathrm dt}\,.$

Also ist die Arbeit nach dem Hauptsatz der Integralrechnung

$W = -\int_{t_1}^{t_2} \frac{\mathrm dV(\mathbf x(t))}{\mathrm dt}\, \mathrm dt= -V(\mathbf x(t_2))+V(\mathbf x(t_1)) = V_1 - V_2\,.$

Dies gilt für alle (stückweise stetig differenzierbare) Bahnen.

Für die Bahnen, die tatsächlich durchlaufen werden, gelten die Newtonschen Bewegungsgleichungen

$\mathbf F=m \frac{\mathrm d}{\mathrm dt}\mathbf v\,.$

Da die Masse m konstant ist, gilt für physikalische Bahnen

$\begin{align} W &= \int_{t_1}^{t_2} \mathbf F(\mathbf x(t)) \cdot \mathbf v(t) \, \mathrm dt = m \int_{t_1}^{t_2} \left(\frac{\mathrm d}{\mathrm dt} \mathbf v(t)\right) \cdot \mathbf v(t) \, \mathrm dt \\ &= m \int_{t_1}^{t_2} \frac{1}{2}\,\frac{\mathrm d}{\mathrm dt} \mathbf v(t)^2 \mathrm dt = \frac{1}{2}\,m\,\mathbf{v}^2(t_2)-\frac{1}{2}\,m\,\mathbf{v}^2(t_1) \\ &= T_2 - T_1 \end{align}$

dass die am Teilchen verrichtete Arbeit seine kinetische Energie

$T = \frac{1}{2}\,m\,\mathbf v^2$

erhöht. Ordnen wir in

V₁ − V₂ = T₂ − T₁

die Terme um, so erhalten wir

$T_1 + V_1 = T_2 + V_2\,.$

Die Summe aus kinetischer und potentieller Energie ist nach der Verschiebung des Körpers noch dieselbe. Dies ist der Energieerhaltungssatz.

Kann, beispielsweise bei einem Pendel, die Reibung vernachlässigt werden, so ändert sich die Summe von potentieller und kinetischer Energie nicht mit der Zeit. Lenkt man das Pendel aus, so schwingt es zwischen zwei Umkehrpunkten und erreicht seine höchste Geschwindigkeit am Ort des Potentialminimums. An den Umkehrpunkten ist die kinetische Energie Null und die potentielle Energie maximal. Unabhängig von der Position des Pendels hat die Summe aus kinetischer und potentieller Energie den durch die anfängliche Auslenkung vorgegebenen Wert.

Energieerhaltungssatz in der Thermodynamik

Jedes thermodynamische System verfügt über einen bestimmten „Vorrat“ an Energie. Dieser setzt sich aus einem äußeren Anteil E_a und einen inneren Anteil E_i (innere Energie) zusammen. Die Summe aus beiden Anteilen ergibt die Gesamtenergie eines thermodynamischen Systems, wobei man in der chemischen Thermodynamik die Änderung des äußeren Anteils gleich Null setzt (dE_a=0). Unter dieser Voraussetzung gelangt man zum ersten Hauptsatz der Thermodynamik:

„Die innere Energie ist eine Eigenschaft der stofflichen Bestandteile eines Systems und kann nicht erzeugt oder vernichtet werden. Die innere Energie ist eine Zustandsgröße.“

Für abgeschlossene Systeme gilt daher, dass die innere Energie konstant und demzufolge ihre Änderung gleich Null ist. Für geschlossene Systeme lautet der erste Hauptsatz der Thermodynamik:

$\qquad \mathrm dU= \delta Q + \delta W$

• U – innere Energie
• Q – Wärme
• W – Arbeit

Energieerhaltungssatz in der Elektrodynamik

Der Satz von Poynting beschreibt die Energieerhaltung in der Elektrodynamik.

Energieerhaltungssatz in der Relativitätstheorie

Ein relativistisches Teilchen der Masse m, das sich mit der Geschwindigkeit v bewegt, hat die Energie

$E(v) = \frac{m\, c^2}{\sqrt{1 - (v/c)^2}}$

wobei c die Lichtgeschwindigkeit ist. In Ruhe beträgt die Energie

$E_{\text{Ruhe}} = m\, c^2\,.$

Für kleine Geschwindigkeiten (Taylorentwicklung in (v / c)²) kommt zur Ruheenergie die Newtonsche kinetische Energie hinzu

$E \sim m\, c^2 +\frac{1}{2}m v^2\,.$

Bei hochenergetischen Teilchen ist diese Näherung messbar falsch. Nur die Summe der relativistischen Energien ist in Teilchenreaktionen erhalten.

Energieerhaltungssatz in der Quantenmechanik

Die Energie quantenmechanischer Zustände ist erhalten, wenn der Hamiltonoperator nicht von der Zeit abhängt. Allerdings sind viele quantenmechanische Zustände, nämliche alle, die sich mit der Zeit messbar ändern, keine Energieeigenzustände. Ihnen kommt nur eine unscharfe Energie zu.

Energieaustausch

Kann ein System Energie mit einem anderen System austauschen, beispielsweise durch Strahlung oder Wärmeleitung, dann spricht man von einem energetisch offenen System. Der Energieerhaltungssatz besagt dabei: Die Energie, die in ein System hineinfließt, minus der Energie, die es verlässt, ist die Änderung der Energie des Systems. Durch Betrachtung der Energieströme des Systems kann man auf Abläufe innerhalb des Systems schließen, auch wenn sie selbst nicht beobachtet werden können.

Die Energie eines Systems lässt sich nicht direkt messen: wenn man von der gravitativen Auswirkung von Energie absieht, so wirken sich nur Energieunterschiede messbar aus.

Noether-Theorem

In der Lagrangeschen Mechanik ergibt sich Energieerhaltung aus dem Noether-Theorem, wenn die Wirkung unter zeitlichen Verschiebungen invariant ist.

Siehe auch

• Konservative Kraft
• Entropie
• Wirkungsgrad

Einzelnachweise

1. ↑ Bohr, Kramers, Slater The quantum theory of radiation, Philosophical Magazine, Bd. 47, 1924, S.785-802, deutsch in Zeitschr. für Physik, Bd. 24, 1924, S.69-87