Euklid'scher Ring

Euklidischer Ring ist ein Fachbegriff aus der Mathematik und bezeichnet einen Ring, in dem eine (verallgemeinerte) Division mit Rest vorhanden ist, wie man sie von den ganzen Zahlen kennt. Die Möglichkeit der Division mit Rest wird dabei durch die Existenz einer geeigneten Bewertungsfunktion gesichert.

Definitionen

Es gibt in der Literatur und in der akademischen und wissenschaftlichen Praxis eine ganze Reihe verschiedener, aber ähnlicher Definitionen eines euklidischen Ringes. Oft sind darin bereits speziellere Eigenschaften enthalten, was z. B. Erleichterungen in der Formulierung der im Weiteren aufgespannten Theorie bringen kann. All diesen Definitionsvarianten ist jedoch gemeinsam, dass ein euklidischer Ring eine Division mit Rest und dadurch einen euklidischen Algorithmus zur Bestimmung des größten gemeinsamen Teilers (ggT) zweier Ringelemente liefert. Von dieser Eigenschaft ist der Name abgeleitet.

Variante 1

Ein Integritätsbereich R (= Integritätsring, also ein kommutativer, nullteilerfreier Ring mit 1) heißt euklidischer Ring, falls eine Bewertungsfunktion 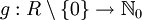$g:R\setminus\{0\}\to \N_0$ existiert mit folgenden Eigenschaften:

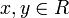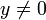• für alle $x,y \in R$ mit $y \neq 0$ existieren Elemente 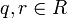$q,r \in R$ mit x = qy + r (Division mit Rest), wobei entweder r = 0 oder g(r) < g(y) ist, und
• für 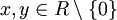$x,y \in R\setminus\{0\}$ gilt stets $g(xy)\ge g(x)$.

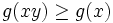Die Abbildung g heißt dabei euklidische Normfunktion (euklidischer Betrag) des Ringes.

Variante 2

Die obenstehende Definition ist fast äquivalent zu der folgenden, ebenfalls häufig verwendeten, in der jedoch zusätzlich eine Bewertung für die Null vorgegeben wird.

Definition:
Ein Integritätsbereich R heißt euklidischer Ring, falls eine Bewertungsfunktion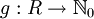 $g:R\to\N_0$ existiert mit folgenden Eigenschaften:

• g(0) = 0,
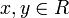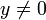• für alle $x,y \in R$ mit $y \neq 0$ existieren Elemente 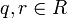$q,r \in R$ mit x = qy + r (Division mit Rest), wobei g(r) < g(y) ist, und
• für 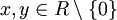$x,y \in R\setminus\{0\}$ gilt stets $g(xy)\ge g(x)$.

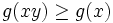Variante 3

Es gibt auch noch eine weitere wesentlich allgemeinere, aber seltener verwendete Variante, in der die Bewertungsfunktion reellwertig ist.

Definition^[1]:
Ein Integritätsbereich R heißt euklidischer Ring, falls eine Wertefunktion (bzw. Bewertungsfunktion)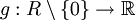 $g:R\setminus\{0\}\to \R$ existiert mit folgenden Eigenschaften:

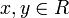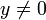• für alle $x,y \in R$ mit $y \neq 0$ existieren Elemente 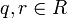$q,r \in R$ mit x = qy + r (Division mit Rest), wobei entweder r = 0 oder g(r) < g(y) ist, und
• zu gegebenen 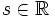$s \in \R$ gibt es höchstens endlich viele reelle Zahlen w_i aus dem Wertebereich 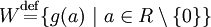$W\stackrel{\mathrm{def}}=\{ g(a) \ | \ a \in R\setminus\{0\} \}$ von g, die kleiner sind als s. In Formeln: 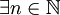$\exists n \in \N$ mit $\operatorname{card}\{w_i \in W | w_i &amp;lt; s\}=n$.

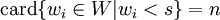Variante 4

Ein besonders schwache Variante liefert die folgende

Definition^[2]:
Ein Integritätsring R (hier nur: ein kommutativer, nullteilerfreier Ring mit wenigstens einem von Null verschiedenem Element) heißt euklidischer Ring, falls eine Gradfunktion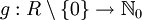 $g:R\setminus\{0\}\to \N_0$ existiert mit folgenden Eigenschaften:

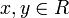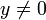• für alle $x,y \in R$ mit $y \neq 0$ existieren Elemente 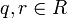$q,r \in R$ mit x = qy + r (Division mit Rest), wobei entweder r = 0 oder g(r) < g(y) ist.

Eigenschaften

• Assoziierte Elemente werden identisch bewertet, insbesondere sind die Einheiten die minimal bewerteten Elemente des Rings.
• Es lässt sich zeigen, dass jeder euklidische Ring eine minimale euklidische Norm besitzt; weiter existiert ein Algorithmus zur iterativen Bestimmung des minimalen euklidischen Betrages in einem euklidischen Ring. Das Finden einer geschlossenen Form für den minimalen euklidischen Betrag ist jedoch im allgemeinen sehr aufwändig.
• Jeder euklidische Ring ist ein Hauptidealring, denn wenn a ein minimal bewertetes Element eines Ideals I ist, so ist I = (a), also ein Hauptideal. Insbesondere ist jeder euklidische Ring faktoriell.

Beispiele für euklidische und nicht euklidische Ringe

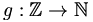• Der Ring $\mathbb{Z}$ der ganzen Zahlen ist ein euklidischer Ring. Die natürlichste Wahl für einen euklidischen Betrag ist $g:\mathbb{Z}\to\mathbb{N}$, $x \mapsto |x|$. Der minimale euklidische Betrag einer ganzen Zahl ist gegeben durch die Länge der Binärdarstellung ihres Absolutbetrages.
• Jeder Körper K ist ein euklidischer Ring mit dem euklidischen Betrag 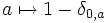$a\mapsto 1 - \delta_{0,a}$, wobei δ das Kronecker-Delta bezeichnet. Dieser Betrag ist auch minimal.
• Der Polynomring K[X] über einem Körper K in einer Variablen X ist ein euklidischer Ring, wobei die euklidische Norm durch den Grad eines Polynoms gegeben ist; dies ist bereits die minimale euklidische Norm.
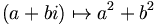• Der Ring $\mathbb{Z}[i]$ der gaußschen Zahlen mit $g:\mathbb{Z}[i]\to \mathbb{N}$ erklärt durch $(a+bi)\mapsto a^{2}+b^{2}$ ist ein euklidischer Ring.
• Dagegen ist z. B. der Polynomring $\mathbb{Z}[X]$ kein euklidischer Ring, da das Ideal (X,2) kein Hauptideal ist.
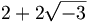• Auch der Ring $\mathbb{Z}[\sqrt{-3}]$ ist nicht euklidisch, da $2+2\sqrt{-3}$ und 4 keinen ggT haben (zwei "maximale gemeinsame Teiler" sind 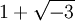$1+\sqrt{-3}$ und 2, die aber teilerfremd sind).

Einzelnachweise

1. ↑ Bernhard Hornfeck: Algebra. S. 142 3.Auflage deGruyter 1976. ISBN 3110067846
2. ↑ Kurt Meyberg: „Algebra – Teil 1“, Carl Hanser Verlag München, Wien.

Literatur

• Bosch: Algebra. 5. Auflage. Springer 2003. ISBN 3-540-40388-4
• Jantzen und Schwermer: Algebra. Springer 2005. ISBN 3-540-21380-5
• Bernhard Hornfeck: Algebra. 3. Auflage. deGruyter 1976. ISBN 3-11-006784-6