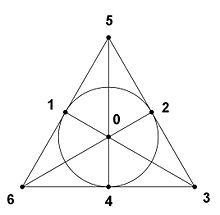
Fano-Ebene

Die Fano-Ebene mit 7 Punkten und 7 Geraden

Die Fano-Ebene ist eine Inzidenzstruktur, die sich sowohl als linearer Raum wie als projektive Ebene oder auch als Blockplan auffassen lässt. Sie ist nach dem italienischen Mathematiker Gino Fano benannt. In der synthetischen Geometrie ist sie das Minimalmodell einer projektiven Ebene. Ihr affiner Ausschnitt, der durch Ausschneiden einer projektiven Geraden entsteht, ist das Minimalmodell einer affinen Ebene.

Daneben werden im Sprachgebrauch der synthetischen Geometrie diejenigen projektiven oder (seltener) affinen Ebenen als Fano-Ebenen bezeichnet, in denen das Fano-Axiom gilt. Die Fano-Ebene, wie sie dieser Artikel beschreibt, ist in diesem axiomatischen Sinn keine Fano-Ebene, denn sie erfüllt das projektive Fano-Axiom nicht.

Definition

Die folgende (symmetrische) Inzidenzstruktur L = (P,G,I) wird als Fano-Ebene bezeichnet:

P = {0,1,2,3,4,5,6}

G = {{1,5,6},{2,3,5},{3,4,6},{0,2,6},{0,1,3},{0,4,5},{1,2,4}}

$I: p\,\text{I}\,g \Leftrightarrow p\in g\quad \text{und} \quad g\,\text{I} \,p \Leftrightarrow p\in g \quad \text{mit} \quad p\in P, g\in G$

Die Fano-Ebene lässt sich durch die Zeichnung eines gleichseitigen Dreiecks mit Höhen und Inkreis visualisieren. Die Elemente von P, auch Punkte genannt, sind dann die drei Eckpunkte, die drei Höhenfußpunkte und der Mittelpunkt des Inkreises. Die Elemente von G, auch Geraden genannt, sind dann die Dreieckseiten, Höhen und der Inkreis (siehe Zeichnung).

Fano-Ebene als projektive Ebene

Die Fano-Ebene ist eine endliche projektive Ebene der Ordnung 2 mit 7 Geraden und 7 Punkten (PG(2,2)). Bei der axiomatischen Beschreibung projektiver Ebenen ergibt sich dies, indem man direkt anhand der gegebenen Inzidenzstruktur die Gültigkeit der Axiome überprüft. Bei der kanonischen Konstruktion einer projektiven Ebene aus einen Vektorraum ($P(\mathbb{Z}_2^3)$) betrachtet man den Vektorraum $\mathbb{Z}_2^3$, dessen 1-dim Unterräume sind dann die Punkte der projektiven Ebene, seine 2-dim Unterräume die Geraden und die Inzidenzrelation ist das mengentheoretische Enthaltensein. Somit erhält man:

Punkte:

$\begin{matrix} \underbrace{\left \{ \begin{pmatrix}1\\1\\0\end{pmatrix},\begin{pmatrix}0\\0\\0\end{pmatrix} \right \}}_{0},& \underbrace{\left \{ \begin{pmatrix}0\\1\\0\end{pmatrix},\begin{pmatrix}0\\0\\0\end{pmatrix} \right \}}_{1},& \underbrace{\left \{ \begin{pmatrix}1\\0\\1\end{pmatrix},\begin{pmatrix}0\\0\\0\end{pmatrix} \right \}}_{2},& \underbrace{\left \{ \begin{pmatrix}1\\0\\0\end{pmatrix},\begin{pmatrix}0\\0\\0\end{pmatrix} \right \}}_{3},& \underbrace{\left \{ \begin{pmatrix}1\\1\\1\end{pmatrix},\begin{pmatrix}0\\0\\0\end{pmatrix} \right \}}_{4},& \underbrace{\left \{ \begin{pmatrix}0\\0\\1\end{pmatrix},\begin{pmatrix}0\\0\\0\end{pmatrix} \right \}}_{5},& \underbrace{\left \{ \begin{pmatrix}0\\1\\1\end{pmatrix},\begin{pmatrix}0\\0\\0\end{pmatrix} \right \}}_{6} \end{matrix}$

Geraden:

$\begin{matrix} \underbrace{\left \{ \begin{pmatrix}0\\0\\1\end{pmatrix},\begin{pmatrix}0\\1\\0\end{pmatrix}, \begin{pmatrix}0\\1\\1\end{pmatrix}, \begin{pmatrix}0\\0\\0\end{pmatrix} \right \}}_{\{1,5,6\}},& \underbrace{\left \{ \begin{pmatrix}1\\0\\0\end{pmatrix},\begin{pmatrix}0\\0\\1\end{pmatrix}, \begin{pmatrix}1\\0\\1\end{pmatrix}, \begin{pmatrix}0\\0\\0\end{pmatrix} \right \}}_{\{2,3,5\}},& \underbrace{\left \{ \begin{pmatrix}1\\0\\0\end{pmatrix},\begin{pmatrix}0\\1\\0\end{pmatrix}, \begin{pmatrix}1\\1\\0\end{pmatrix}, \begin{pmatrix}0\\0\\0\end{pmatrix} \right \}}_{\{0,3,1\}},& \underbrace{\left \{ \begin{pmatrix}1\\0\\1\end{pmatrix},\begin{pmatrix}0\\1\\0\end{pmatrix}, \begin{pmatrix}1\\1\\1\end{pmatrix}, \begin{pmatrix}0\\0\\0\end{pmatrix} \right \}}_{\{1,2,4\}},\\ \underbrace{\left \{ \begin{pmatrix}1\\0\\0\end{pmatrix},\begin{pmatrix}0\\1\\1\end{pmatrix}, \begin{pmatrix}1\\1\\1\end{pmatrix}, \begin{pmatrix}0\\0\\0\end{pmatrix} \right \}}_{\{3,4,6\}},& \underbrace{\left \{ \begin{pmatrix}1\\1\\0\end{pmatrix},\begin{pmatrix}0\\0\\1\end{pmatrix}, \begin{pmatrix}1\\1\\1\end{pmatrix}, \begin{pmatrix}0\\0\\0\end{pmatrix} \right \}}_{\{0,4,5\}},& \underbrace{\left \{ \begin{pmatrix}1\\1\\0\end{pmatrix},\begin{pmatrix}0\\1\\1\end{pmatrix}, \begin{pmatrix}1\\0\\1\end{pmatrix}, \begin{pmatrix}0\\0\\0\end{pmatrix} \right \}}_{\{0,2,6\}} \end{matrix}$

Die so konstruierte Inzidenzstruktur ist zur obigen Definition isomorph. Als projektive Ebene (2-dimensionaler projektiver Raum) der Ordnung 2 ist die Fano-Ebene auch ein linearer Raum, da dessen Axiome in den Axiomen eines projektiven Raums enthalten sind, sowie ein symmetrischer 2-(7,3,1) Blockplan.

Die Automorphismengruppe der Fano-Ebene ist transitiv auf den geordneten nichtkollinearen Tripeln und hat daher die Ordnung 7*6*4 = 168. Sie ist nichtabelsch und einfach (d. h. sie hat nur die trivialen Normalteiler).

Literatur

• J.H. van Lint, R.M. Wilson: A Course in Combinatorics. Cambridge University Press, 1992, ISBN 0-521-42260-4, S. 197

Weblinks

• Eric W. Weisstein: Fano Plane. In: MathWorld. (englisch)
• Endliche Ebene und Fano-Ebene bei PlanetMath (engl.)