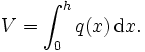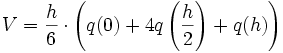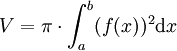- Fassregel
-
Die Keplersche Fassregel (nach Johannes Kepler) ist eine Methode zur näherungsweisen Berechnung von Integralen.
Nachdem 1611 Keplers erste Frau in Prag gestorben war, heiratete er – nun in Linz arbeitend – 1613 wieder. Er kaufte für die Hochzeit einige Fässer Wein. Als der Wein eingekellert war, kam der Verkäufer mit einer Messrute und bestimmte den Inhalt für alle Fässer ohne Überlegung oder Rechnung nach der gleichen Methode. Die Messrute wurde mit ihrer metallenen Spitze durch das Spundloch quer bis zu den Rändern der beiden Böden eingeführt und die Marke am Spundloch ergab den Rauminhalt. Kepler wunderte sich, dass eine Diagonale durch die Fasshälfte ein Maß für den Rauminhalt abgeben sollte und bezweifelte die Richtigkeit dieser Methode, da ein sehr niedriges Fass mit etwas breiteren Böden und daher sehr viel kleinerem Rauminhalt die gleiche Visierlänge besitzen könnte.
Kepler verfasste daraufhin die Schrift Nova Stereometria doliorum vinariorum 1615 (Neue Inhaltsberechnung von Weinfässern), in der er nach überprüfbaren Methoden zur Inhaltsberechnung von Weinfässern suchte. Eine dieser Methoden bestand darin, die Krümmung des Fasses durch eine Parabel anzunähern, da Inhaltsberechnungen mit Hilfe von Parabeln seit Archimedes exakt durchgeführt werden konnten.
Unter anderem beschrieb er darin eine Formel zur Berechnung der Kapazität (genauer des Volumens) von Weinfässern mit unregelmäßigen Formen. Diese Formel liefert exakte Werte für den Pyramidenstumpf (einschließlich Pyramide), Kugel, elliptisches Paraboloid, einschaliges Hyperboloid und alle anderen Körperschichten, die sich durch ebene Körperschnitte senkrecht zu den Körperachsen erzeugen lassen. Da die Keplersche Fassregel für das Volumen von Pyramide und Tetraeder präzise Resultate ergibt, ist sie auch für Prismoide fehlerfrei anwendbar. Gute Näherungswerte liefert sie für Fässer und tonnenförmige Körper und nicht zu lange Baumstämme. Eine größere Genauigkeit kann in kritischen Fällen durch einen größeren Messaufwand erreicht werden, indem man die Messhöhe h in n = 2k gleiche Teile zerlegt und für die entstandenen k Schichtenpaare je einmal die Keplersche Fassregel anwendet. (siehe Simpsonsche Formel)
Flächenberechnung
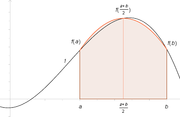
Wenn man die Funktion f(x) durch eine Parabel g(x), bestimmt durch die drei Punkte
annähert, so gilt:
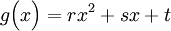 ,
,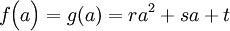 ,
,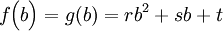 und
und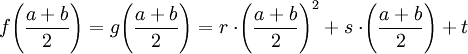
Damit wird
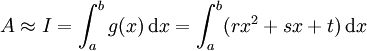
![=[\frac{1}{3} rx^3+ \frac{1}{2} sx^2+tx ]_a^b](/pictures/dewiki/99/cd8b1d3f41491943ae1da5137972e6ce.png)
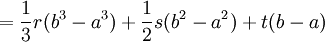
Wegen (b3 − a3) = (b − a)(b2 + ab + a2) kann b-a ausgeklammert werden. Dies ergibt
![=\frac{1}{6} (b-a)[2r(a^2 + ab + b^2) + 3s(a+b)+6t]](/pictures/dewiki/102/fd0ed59404033de7f4852ae1449ac328.png)
![=\frac{1}{6} (b-a)[(ra^2+sa+t)+(rb^2+sb+t)+r(a^2+2ab+b^2)+2s(a+b)+4t]](/pictures/dewiki/56/82f99e67c6d6d671a5ab8dadeb2f503d.png)
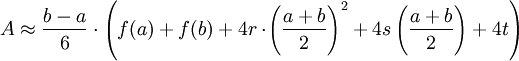
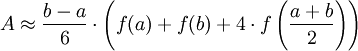
Ist f ein Polynom höchstens dritten Grades, so ist die Fläche sogar gleich A.
Volumenberechnung
Der Name Fassregel lässt sich durch die folgende Anwendung begründen: Zur Berechnung des Volumens eines Weinfasses sei q(x) die Querschnittsfläche quer zur Längsachse in der Entfernung x vom Boden des Fasses; sie lässt sich durch Bestimmung des Umfanges leicht ausrechnen. Ist h die Höhe des Fasses, so ist das Volumen gleich
Die Keplersche Fassregel gibt nun
als Näherungswert für das Volumen eines Körpers, dessen Querschnitt an drei Stellen bekannt ist. Ist der Körper ein Rotationskörper, so gilt bei Rotation um die x-Achse:
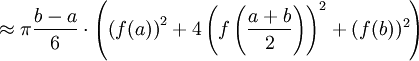
Für bestimmte Rotationskörper wie Kegel und Kegelstumpf, Zylinder und Rotationsparaboloid gibt diese Formel das genaue Volumen an.
Ist u der Umfang von Boden und Deckel und U der Umfang in der Mitte des Fasses, so ergibt sich daraus die Näherungsformel:
![\frac{h}{6}\cdot \left[ 2\pi \left( {\frac{u}{2\pi}} \right)^2 + 4 \left( {\frac{U}{2\pi}} \right)^2 \pi \right] \
= \ \frac{h}{6}\cdot \left[ 2\pi \left( \frac{u^2}{4\pi^2} \right) + 4 \left( \frac{U^2}{4\pi^2} \right) \pi \right]](/pictures/dewiki/48/00d51b1bf76e6b332ca72af164b7fc6d.png)
![=\frac h{12\pi}\cdot \left[u^2 + 2U^2\right].](/pictures/dewiki/53/58ea1c424bce4ef468eba83b485cfef0.png)
Der genaue Wert für eine parabolische Krümmung der Fassdauben ist
![\frac{h}{60\pi}\cdot \left[3u^2 + 4Uu + 8 U^2 \right].](/pictures/dewiki/53/55cee940437b321ddaaa04fb314c6af4.png)
Siehe auch
Wikimedia Foundation.