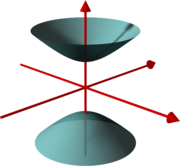
- Einschaliges Hyperboloid
-
Ein Hyperboloid ist eine Fläche zweiter Ordnung, die durch Ebenen in Hyperbeln, Ellipsen, Parabeln geschnitten werden kann.
Es wird zwischen ein- und zweischaligen Hyperboloiden unterschieden.
Das einschalige Hyperboloid gleicht einem Kühlturm, auf der Oberfläche liegen zwei Scharen von Geraden. Daher ist das einschalige Hyperboloid eine Regelfläche. Jede Tangentialebene T schneidet das Hyperboloid in zwei Geraden, deren Schnittpunkt der Berührpunkt von T ist.
Das zweischalige Hyperboloid besteht aus zwei nicht miteinander verbundenen Teilflächen, es enthält keine reellen Geraden.
Die Formel für ein Hyperboloid ist:
- einschalig:
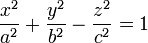
- zweischalig:
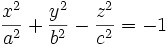
Der Grenzfall zwischen ein- und zweischaligen Hyperboloiden, wenn sich die beiden Schalen in einem Punkt berühren, ist der Doppelkegel:
- Doppelkegel:
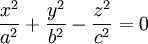
Ein Hyperboloid mit a = b wird auch als Rotationshyperboloid bezeichnet.
Parametrisierung
Es gibt verschiedene Möglichkeiten ein Hyperboloid mit einer Funktion
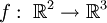 zu parametrisieren. Eine einfache Möglichkeit ist die Folgende, wobei d = 1 ein einschaliges, d = − 1 ein zweischaliges Hyperboloid und d = 0 einen Doppelkegel liefert:
zu parametrisieren. Eine einfache Möglichkeit ist die Folgende, wobei d = 1 ein einschaliges, d = − 1 ein zweischaliges Hyperboloid und d = 0 einen Doppelkegel liefert: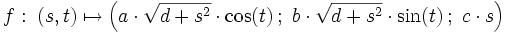
Die erste hyperboloide Struktur in der Welt hat Wladimir Schuchow 1896 gebaut.
Weblinks
- einschalig:
Wikimedia Foundation.