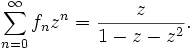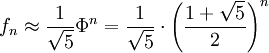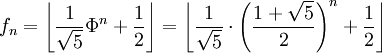- Formel von Binet
-
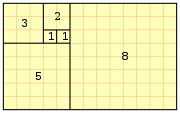
Die Fibonacci-Folge ist eine unendliche Folge von Zahlen (den Fibonacci-Zahlen), bei der sich die jeweils folgende Zahl durch Addition der beiden vorherigen Zahlen ergibt: 0, 1, 1, 2, 3, 5, 8, 13, … Benannt ist sie nach Leonardo Fibonacci, der damit 1202 das Wachstum einer Kaninchenpopulation beschrieb. Die Reihe war aber schon in der indischen und westlichen Antike bekannt.
Inhaltsverzeichnis
Definition der Fibonacci-Folge
Die Fibonacci-Folge
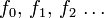 , benannt nach Leonardo Fibonacci, ist durch das rekursive Bildungsgesetz
, benannt nach Leonardo Fibonacci, ist durch das rekursive Bildungsgesetz für
für 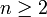
mit den Anfangswerten
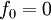 und
und 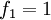
definiert. Das bedeutet in Worten:
- Für die beiden ersten Zahlen werden die Werte null und eins vorgegeben.
- Jede weitere Zahl ist die Summe ihrer beiden Vorgänger.
Daraus ergibt sich die Folge zu
- 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1.597, 2.584, 4.181, 6.765, 10.946, 17.711, 28.657, … (Folge A000045 in OEIS)
Oft wird auch f0 = 0 ausgelassen und die Fibonacci-Folge mit f1 = 1 und f2 = 1 beginnend definiert, insbesondere bei der Anwendung auf Situationen, in denen ein Anfangswert Null keinen Sinn hat.
Eigenschaften
Beziehungen zwischen den Folgegliedern
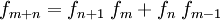
 mit der Lucas-Folge
mit der Lucas-Folge 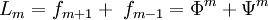 , insbesondere:
, insbesondere: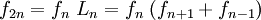
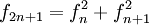
 (Identität von Catalan)
(Identität von Catalan)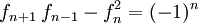 (Identität von Cassini, Spezialfall der Catalan-Identität)
(Identität von Cassini, Spezialfall der Catalan-Identität)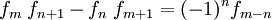 (Identität von d’Ocagne)
(Identität von d’Ocagne)

- Je zwei benachbarte Fibonaccizahlen sind teilerfremd, d.h.
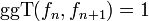 .
. 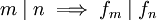 ; falls m > 2 ist, gilt auch die Umkehrung. Insbesondere kann fn für n > 4 nur dann eine Primzahl sein, wenn n eine Primzahl ist.
; falls m > 2 ist, gilt auch die Umkehrung. Insbesondere kann fn für n > 4 nur dann eine Primzahl sein, wenn n eine Primzahl ist.
Es gibt noch zahlreiche weitere derartige Formeln.
Verwandtschaft mit dem Goldenen Schnitt
Wie von Johannes Kepler festgestellt wurde, nähert sich der Quotient zweier aufeinander folgender Fibonacci-Zahlen dem Goldenen Schnitt Φ an. Dies folgt unmittelbar aus der Näherungsformel für große n:
Diese Quotienten zweier aufeinander folgender Fibonacci-Zahlen haben eine bemerkenswerte Kettenbruchdarstellung
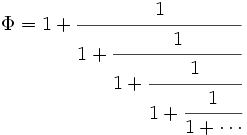
Da diese Quotienten im Grenzwert gegen den goldenen Schnitt konvergieren, lässt sich dieser als der unendliche Kettenbruch
darstellen.
Φ ist eine irrationale Zahl. Es zeigt sich, dass sie in einem bestimmten Sinne die irrationalste aller Zahlen ist. Das bedeutet, dass sie sich nur schlecht durch ein Verhältnis zweier ganzer Zahlen annähern lässt, ein Umstand, der wesentlich zu ihrer Bedeutung in Kunst und Natur beiträgt. Am besten lässt sich Φ durch Quotienten zweier aufeinander folgender Fibonacci-Zahlen darstellen. Dies gilt auch für entartete Fibonaccifolgen, bei denen f0 und fn beliebige natürliche Zahlen annehmen.
Zeckendorf-Theorem
Das Zeckendorf-Theorem (nach Edouard Zeckendorf) besagt, dass jede natürliche Zahl n größer Null eindeutig als Summe voneinander verschiedener, nicht direkt aufeinanderfolgender Fibonacci-Zahlen geschrieben werden kann. Das heißt, es gibt für jedes
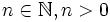 eine eindeutige Darstellung der Form
eine eindeutige Darstellung der FormDie entstehende Folge (c) von Nullen und Einsen wird Zeckendorf-Sequenz genannt. Da aufeinanderfolgende Fibonacci-Zahlen ausgeschlossen sind, können keine zwei Einsen in einer Zeckendorf-Sequenz unmittelbar hintereinander stehen.
Fibonacci-Folgen in der Natur
Viele Pflanzen weisen in ihrem Bauplan Spiralen auf, deren Anzahl durch Fibonacci-Zahlen gegeben sind, wie beispielsweise bei den Samen in Blütenständen. Das ist dann der Fall, wenn der Winkel zwischen architektonisch benachbarten Blättern oder Samen bezüglich der Pflanzenachse der Goldene Winkel ist. Hintergrund ist der Umstand, dass die rationalen Zahlen, die den zugrunde liegenden Goldenen Schnitt am besten approximieren, Brüche von aufeinanderfolgenden Fibonacci-Zahlen sind. Die Spiralen werden daher von Pflanzenelementen gebildet, deren Platznummern sich durch die Fibonacci-Zahl im Nenner unterscheiden und damit fast in die gleiche Richtung weisen.
Durch diese spiralförmige Anordnung der Blätter um die Sprossachse erzielt die Pflanze die beste Lichtausbeute. Der Versatz der Blätter um das irrationale Verhältnis des Goldenen Winkels sorgt dafür, dass nie Perioden auftauchen, wie es z. B. bei 1/4 der Fall wäre (0° 90° 180° 270° | 0° 90° …). Dadurch wird der denkbar ungünstigste Fall vermieden, dass ein Blatt genau senkrecht über dem anderen steht und sich so die jeweils übereinanderstehenden Blätter maximalen Schatten machen oder maximale ‚Lichtlücken‘ entstehen. Wissenschaftshistorisch ist hierfür das Buch On Growth and Form von D'Arcy Wentworth Thompson (1917) grundlegend.
Ein weiterer interessanter Aspekt ist, dass die Fibonacci-Folge die Ahnenmenge einer weiblichen Honigbiene (Apis mellifera) beschreibt. Das erklärt sich dadurch, dass Bienendrohnen sich aus unbefruchteten Eiern entwickeln, die in ihrem Genom dem Erbgut der Mutter entsprechen.
Berechnung
Formel von Moivre-Binet
Das explizite Bildungsgesetz für die Glieder der Fibonacci-Folge gelang unabhängig voneinander den französischen Mathematikern Abraham de Moivre im Jahr 1730 und Jacques Philippe Marie Binet im Jahr 1843. Das Ergebnis war aber auch schon den Mathematikern Leonhard Euler und Daniel Bernoulli bekannt.
Die Fibonacci-Zahlen lassen sich direkt mittels
berechnen, wobei
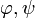 die beiden Lösungen der Gleichung x2 − x − 1 = 0 sind. Setzt man
die beiden Lösungen der Gleichung x2 − x − 1 = 0 sind. Setzt man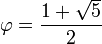 und
und 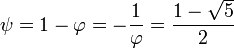
ein, erhält man die geschlossene Formel von Moivre-Binet
Bemerkenswert ist das Zusammenspiel zweier irrationaler Zahlen
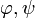 , das zu einem ganzzahligen Ergebnis führt.
, das zu einem ganzzahligen Ergebnis führt.Herleitung der Formel von Moivre-Binet
Die Formel von Binet kann mit Matrizenrechnung und dem Eigenwertproblem in der Linearen Algebra hergeleitet werden, folgender Ansatz:
Um das Problem zu lösen, transformiert man die Matrix
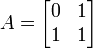 in eine Diagonalmatrix D durch Betrachtung als Eigenwertproblem.
in eine Diagonalmatrix D durch Betrachtung als Eigenwertproblem.Es gilt A = TDT − 1, wobei T die Matrix der Eigenvektoren und D die Diagonalmatrix mit den Eigenwerten ist. Das Problem kann nun wie folgt geschrieben werden und führt zur Lösung:
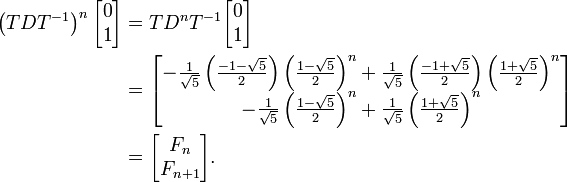
Eine zweite Herleitung
Eine andere Möglichkeit erhält man durch folgenden Ansatz:
Für die Potenzfunktion p(n) = xn gilt für alle
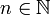
- p(n + 2) − p(n + 1) − p(n) = (x2 − x − 1)p(n)
durch Herausheben.
Wenn also x so gewählt wird, dass x2 − x − 1 = 0 ist, wird p(n + 2) = p(n + 1) + p(n), also die Rekursion der Fibonaccifolge. Das tritt ein, wenn x das reziproke Teilverhältnis Φ des goldenen Schnitts oder sein algebraisch Konjugiertes Ψ ist. Die Fibonaccische Rekursionsformel wird also auch erfüllt durch g(n) = aΦn + bΨn.
Nun bestimme man die Koeffizienten a und b so, dass wie bei der Fibonaccifolge g(0) = 0 und g(1) = 1 wird. Dazu sind zwei einfache lineare Gleichungen zu lösen. Dann kommt die Binet-Formel heraus.
Erzeugende Funktion
Die erzeugende Funktion der Fibonacci-Zahlen ist
Die auf der linken Seite stehende Potenzreihe konvergiert für | z | < 1 / Φ. Über die Partialbruchzerlegung erhält man wiederum die Formel von Moivre-Binet.
Schreibt man die obige erzeugende Funktion als Verknüpfung zweier Potenzreihen im Sinne der formalen Potenzreihen so erhält man
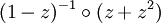 . Als Potenzreihe geschrieben ergibt das
. Als Potenzreihe geschrieben ergibt das 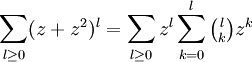 nach Umformungen dieser Summe zu einer Binomialreihe. Die letzte Summe kann mittels Umbenennung der Summationsindizes vereinfacht werden zu
nach Umformungen dieser Summe zu einer Binomialreihe. Die letzte Summe kann mittels Umbenennung der Summationsindizes vereinfacht werden zu  .
.Koeffizientenvergleich liefert für
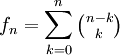 .
.Darstellung mit Matrizen
Die Fibonacci-Zahlen tauchen auch als Einträge der Potenzen der Matrix
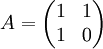 auf:
auf:Aus der Relation Am + n = AmAn ergibt sich beispielsweise die erste oben angegebene Formel für fm + n. A beschreibt zugleich die Summationsvorschrift der Fibonacci-Folge, denn ihr Produkt mit einem Paar aufeinanderfolgender Fibonacci-Zahlen (als Spaltenmatrix geschrieben) ergibt das nächste Paar; entsprechend erzeugt An das n-te Paar aus dem Startpaar (0,1). Dies und die Tatsache, dass die Eigenwerte von A gerade der Goldene Schnitt und dessen Kehrwert (Letzterer mit negativem Vorzeichen) sind, führen wieder auf die oben genannte Formel von Binet.
Näherungsformel für große Zahlen
Für große Werte von n wird der Ausdruck
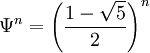 in der Formel von Binet immer kleiner, da der Ausdruck vom Betrag < 1 ist. Deshalb erhält man die Näherungsformel
in der Formel von Binet immer kleiner, da der Ausdruck vom Betrag < 1 ist. Deshalb erhält man die NäherungsformelIm Unterschied beispielsweise zur Stirling-Formel wird diese Formel für wachsende n immer genauer; bei der Stirling-Formel geht lediglich der relative Fehler gegen 0.
Der Absolutbetrag des Quotienten
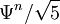 ist für alle n kleiner als 0,5. Demnach beschreibt die Näherungsformel das exakte Ergebnis mit einem Fehler von weniger als 0,5. Durch Runden kommt man daher wieder zu einer exakten Formel:
ist für alle n kleiner als 0,5. Demnach beschreibt die Näherungsformel das exakte Ergebnis mit einem Fehler von weniger als 0,5. Durch Runden kommt man daher wieder zu einer exakten Formel:mit der Gaußklammer
 .
.Geschichte
Ihre früheste Erwähnung findet sich unter dem Namen maatraameru („Berg der Kadenz“) in der Chhandah-shāstra („Kunst der Prosodie“) des Sanskrit-Grammatikers Pingala (um 450 v. Chr. oder nach anderer Datierung um 200 v. Chr.)[1]. In ausführlicherer Form behandelten später auch Virahanka (6. Jh.) und besonders dann Acharya Hemachandra (1089–1172) diese Zahlenfolge, um die rechnerische Möglichkeit der Bildung von Metren durch regelmäßige Verteilung kurzer und langer Silben zu beschreiben.
In der westlichen Welt war diese Reihe ebenfalls schon in der Antike Nikomachos von Gerasa (um 100 n. Chr.) bekannt.[2] Sie ist aber mit dem Namen des italienischen Mathematikers Leonardo da Pisa, genannt Fibonacci („figlio di Bonacci“, Sohn des Bonacci), verbunden, der in seinem Liber abbaci („Buch der Rechenkunst“, Erstfassung von 1202 nicht erhalten, zweite Fassung von ca. 1227) diese Zahlenfolge mit dem Beispiel eines Kaninchenzüchters beschrieb, der herausfinden will, wie viele Kaninchenpaare innerhalb eines Jahres aus einem einzigen Paar entstehen, wenn jedes Paar ab dem zweiten Lebensmonat ein weiteres Paar pro Monat zur Welt bringt[3]:
Modell einer Kaninchenpopulation
Fibonacci illustrierte diese Folge durch die einfache mathematischen Modellierung des Wachstums einer Kaninchenpopulation nach folgender Vorschrift:
- Zu Beginn gibt es ein Paar geschlechtsreifer Kaninchen.
- Jedes neugeborene Paar wird im zweiten Lebensmonat geschlechtsreif.
- Jedes geschlechtsreife Paar wirft pro Monat ein weiteres Paar.
- Die Tiere befinden sich in einem abgeschlossenen Raum („in quodam loco, qui erat undique pariete circundatus“), so dass kein Tier die Population verlassen und keines von außen hinzukommen kann.
Das erste Paar erzeugt seinen Nachwuchs bereits im ersten Monat. Jeden Folgemonat kommt dann zu der Anzahl der Paare, die im letzten Monat gelebt haben, eine Anzahl von neugeborenen Paaren hinzu, die gleich der Anzahl der Paare ist, die bereits im vorletzten Monat gelebt haben, da genau diese geschlechtsreif sind und sich nun vermehren. Fibonacci führte den Sachverhalt für die zwölf Monate eines Jahres vor (1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377) und weist auf die Bildung der Reihe durch Addition mit dem jeweils vorhergehenden Reihenglied hin (1+2=3, 2+3=5, 3+5=8, etc.). Er merkte außerdem an, dass die Folge sich − unter der Annahme unsterblicher Kaninchen − unendlich fortsetzen lässt: „et sic posses facere per ordinem de infinitis numeris mensibus.“ Weitere Beachtung hatte er dem Prinzip in seinen erhaltenen Werken nicht geschenkt.
Nachdem spätere Mathematiker wie Gabriel Lamé (1795–1870) die Entdeckung dieser Zahlenfolge für sich beansprucht hatten, brachten Édouard Lucas (1842–1891)[4] und andere wieder in Erinnerung, dass der zu dieser Zeit älteste bekannte Beleg von Leonardo da Pisa stammte, und unter dem Namen „Fibonacci-Folge“ („suite de Fibonacci“, „Fibonacci sequence“, „successione di Fibonacci“) ist sie seither in den meisten westlichen Sprachen geläufig geworden.
Rezeptionen in Kunst und Unterhaltung
- Das Systemgedicht alfabet (1981) der dänischen Schriftstellerin Inger Christensen basiert auf der Fibonacci-Folge.
- Die Rock-Band Tool bedient sich in ihrem Song Lateralus (vom gleichnamigen Album von 2001) der Fibonacci-Folge und lässt die Silben der Strophentexte im entsprechenden Rhythmus erklingen.
- Die Fibonacci-Folge findet Erwähnung in Dan Browns Roman Sakrileg und im Roman Der Kern des Bösen von Tiberius Maczek (2007). Außerdem in Katherine Nevilles Roman Das Montglane-Spiel (Originaltitel: The Eight, 1988).
- Des Weiteren ist diese Folge im Film Pi relevant und wird ebenfalls in der Serie Taken erwähnt.
- Der Künstler Mario Merz setzte sich in seinen Installationen mit der Fibonacci-Folge auseinander.
- In der Fernsehserie Fringe kommt der Fibonacci-Folge eine Schlüsselrolle zu.
Siehe auch
Literatur
- Hans Magnus Enzensberger, Der Zahlenteufel, ISBN 3-446-18900-9.
- John H. Conway und Richard K. Guy, The Book of Numbers, ISBN 0-387-97993-X.
- Paulo Ribenboim: The New Book of Prime Number Records, ISBN 0-387-94457-5.
Weblinks
- Fibonacci-Zahlen − sehr ausführliche Seite mit weiterführenden Themen
- Fibonacci Numbers and the Golden Section (englisch)
- Fibonacci und der Goldene Schnitt (PDF)
- Fibonacci-Zahlen bei Brettspielen
- Video: Die Fibonacci-Zahlen (aus der Fernsehsendung Mathematik zum Anfassen des Senders BR-alpha) von Albrecht Beutelspacher
Einzelnachweise
- ↑ Parmanand Singh: Acharya Hemachandra and the (so called) Fibonacci Numbers. In: Mathematics Education 20,1 (Siwan, 1986), S. 28–30, ISSN 0047-6269]
- ↑ Friedrich Gustav Lang: Schreiben nach Mass. Zur Stichometrie in der antiken Literatur. In: Novum Testamentum, Vol. 41, Fasc. 1, 1999, S. 40-57. Lang verweist S. 55, Fußnote 86, auf Nikomachos von Gerasa, der diese Reihe neben anderen Zahlenreihen aufgelistet habe.
- ↑ Baldassare Boncompagni (Hrsg.): Scritti di Leonardo Pisano matematico del secolo decimoterzo, Bd. I, Tipografia delle scienze matematiche e fisiche, Rom, 1857, S. 283–284 (Kap. XII, 7: „Quot paria coniculorum in uno anno ex uno pario germinentur“)
- ↑ Edouard Lucas: Recherches sur plusieurs ouvrages de Léonard de Pise et sur diverses questions d’arithmétique supérieure. In: Bulletino di bibliografia e di storia delle scienze matematiche e fisiche 10 (1877), S. 129–193, S. 239–293
Wikimedia Foundation.

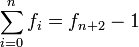
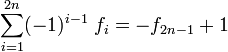

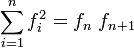
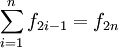
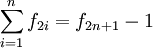
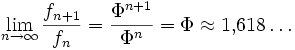
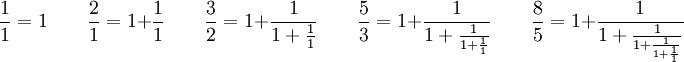
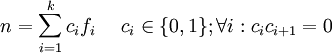


![f_n = \frac 1{\sqrt 5} \left[ \left(\frac{1+\sqrt 5}2\right)^n - \left(\frac{1-\sqrt 5}2\right)^n \right].](/pictures/dewiki/99/cf9e689b7872d81c0655a10eaf38aa32.png)