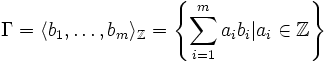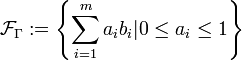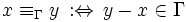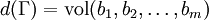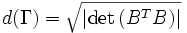Gittervektor

Ausschnitt eines Gitters. Die blauen Punkte gehören zum Gitter.

In der Mathematik sind Gitter in gewissem Sinne regelmäßige Mengen. Sie finden u. a. Anwendung in der Gruppentheorie und der Geometrie. Die einzelnen Elemente eines Gitters heißen Gitterpunkte oder Gittervektoren.

Gitter im euklidischen Raum

Es sei 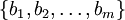$\{b_1, b_2, \ldots, b_m\}$ eine Familie linear unabhängiger Vektoren des euklidischen Raums $\mathbb{R}^n$. Dann heißt

$\Gamma = \langle b_1,\dots,b_m \rangle_\mathbb{Z} = \left\{\sum\limits_{i=1}^ma_ib_i | a_i\in\mathbb{Z}\right\}$

ein Gitter mit Basis 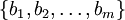$\{b_1, b_2, \ldots, b_m\}$ vom Rang m. Es heißt 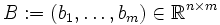$B:=(b_1,\dots,b_m)\in\mathbb{R}^{n\times m}$ eine Basismatrix von Γ. Der Rang eines Gitters ist von der Wahl der Basis unabhängig. Γ ist eine freie abelsche Gruppe vom Rang m.

Die kompakte Menge

$\mathcal{F}_\Gamma := \left\{\sum\limits_{i=1}^ma_ib_i | 0\leq a_i\leq 1\right\}$

heißt die Grundmasche oder Fundamentalmasche von Γ.

Man kann auf $\mathbb{R}^n$ mittels eines Gitters Γ eine Äquivalenzrelation wie folgt definieren:

$x\equiv_\Gamma y \,:\Leftrightarrow\, y-x\in\Gamma$

Demnach sind zwei Punkte äquivalent modulo Γ, wenn sie relativ zum Ursprung ihrer Masche die gleiche Position einnehmen.

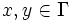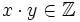Ein Gitter Γ heißt ganz, falls für alle $x, y \in \Gamma$ gilt: $x \cdot y \in \mathbb{Z}$, gilt zudem noch: 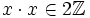$x \cdot x \in 2\mathbb{Z}$ spricht man von einem geradem Gitter.

Gitter in der komplexen Zahlenebene

Indem man die komplexe Zahlenebene $\mathbb C$ als reellen Vektorraum auffasst, kann man von Gittern in $\mathbb C$ sprechen; sie sind freie abelsche Gruppen vom Rang 2. Sie spielen eine zentrale Rolle in der Theorie der elliptischen Funktionen und elliptischen Kurven.

Ist allgemeiner g eine natürliche Zahl, so stehen Gitter im reell 2g-dimensionalen Raum 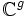$\mathbb C^g$ in Beziehung zu komplexen Tori und abelschen Varietäten.

Beispiele

• Sei Γ das zur Basismatrix 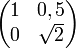$\begin{pmatrix}1 & 0,5 \\ 0 & \sqrt{2}\end{pmatrix}$ gehörige Gitter vom Rang 2. Dann ist $\det\Gamma = \sqrt{2}$.
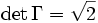• Sei 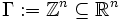$\Gamma:=\mathbb{Z}^n\subseteq\mathbb{R}^n$. Dann ist die Grundmasche von Γ der n-dimensionale Hyperwürfel $\mathcal{F}_\Gamma=[0,1]^n$, und es gilt z. B. $(1.5, 0, \dots, 0)\equiv_\Gamma (-3.5, 1, \dots, 1)$.
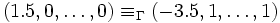• Der Ring der gaußschen Zahlen $\mathbb{Z}[\mathrm{i}]$ ist ein Gitter in $\mathbb{C}$.

Gitterdiskriminante

Eine Kenngröße zur Klassifikation von Gittern ist die Gitterdiskriminante. Sie berechnet sich als Volumen der Grundmasche.

$d(\Gamma) = \operatorname{vol}(b_1,b_2,\ldots,b_m)$

Bei Gittern im euklidischen Raum mit der Basismatrix B entspricht dies der Formel

$d(\Gamma) = \sqrt{\left|\det\left(B^TB\right)\right|}$

Als Invariante ist der Wert der Gitterdiskrimante unabhängig von der gewählten Basis.

Gitterreduktion

Die Gitterreduktion ist das Problem, aus einer gegebenen Gitterbasis eine Basis mit gewissen Eigenschaften zu berechnen, wie zum Beispiel eine Basis mit kurzen, nahezu orthogonalen Vektoren. Der LLL-Algorithmus (nach Lenstra, Lenstra und Lovász) berechnet in polynomieller Zeit eine sogenannte LLL-reduzierte Basis, mit deren Hilfe man sehr kurze Gittervektoren erhält. In der Tat liegt die Länge des ersten Vektors einer LLL-reduzierten Basis sehr nah an der Länge des kürzesten nichttrivialen Gittervektors.

Der LLL-Algorithmus hat zahlreiche Anwendungen in der Kryptoanalyse von asymmetrischen Verschlüsselungsverfahren, wie dem RSA-Kryptosystem und dem Merkle-Hellman-Kryptosystem, gefunden.

Literatur

• Oded Regev: Lattices in Computer Science. Tel-Aviv University, 2004

Siehe auch

• Raumgruppe
• Bravais-Gitter
• Spezielle Gitter werden nach Dedekind bei der Untersuchung algebraisch ganzer Zahlen verwendet. Siehe dazu Ordnung (algebraische Zahlentheorie)