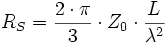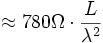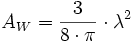HERTZscher Dipol

Richtcharakteristik eines hertzschen Dipols (rote Linie).

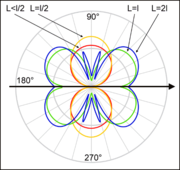
Der hertzsche Dipol (nach Heinrich Hertz), auch Elementardipol genannt, ist ein verlustarmer, angepasster elektrischer Strahler mit homogener Stromverteilung. Er ist ein Linearstrahler mit einer Länge L deutlich kleiner als die Wellenlänge λ, worin er sich von einem Dipolstrahler unterscheidet. Gegenüber einem Kugelstrahler hat er bereits eine Richtwirkung (rote Kurve in der Zeichnung) und eine Polarisation. Demgegenüber ist die Richtcharakteristik eines Dipolstrahlers mit
L = λ / 2 etwas ausgeprägter (gelbe Kurve).

Der hertzsche Dipol ist eine Bezugsantenne, wird aber zum Vergleich selten herangezogen. Gegenüber dem Kugelstrahler hat er wegen seiner Richtwirkung bereits einen Gewinn von 1,5 (oder 1,76 dB. Zum Vergleich: λ / 2-Dipol: 2,2 dB). Praktisch realisiert werden kann der hertzsche Dipol als verkürzter Halbwellendipol
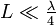($L\ll\tfrac{\lambda}{4}$ ) mit Dachkapazitäten, welcher über ein Anpassungsglied gespeist wird.

Der Herzsche Dipol entsteht aus dem Ansatz einer harmonisch oszillierenden Ladungs- und Stromverteilung

$\rho (\mathbf x, t)=\rho(\mathbf x)\mathrm e^{-\mathrm i\omega t}$

$\mathbf j(\mathbf x, t)=\mathbf j(\mathbf x)\mathrm e^{-\mathrm i\omega t}$

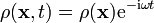
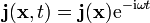
wobei bei der Berechnung des Vektorpotentials nur der erste Summand beachtet wird, und zudem 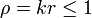$\rho=k r\leq 1$ angenommen wird.

Elektrisches und magnetisches Feld des Herzschen Dipol sind

$\mathbf H = \frac{ck^3}{4\pi}(\mathbf n \times \mathbf p)\frac{\mathrm{e}^{\mathrm{i} \rho}}{\rho} \left(1+\frac{\mathrm{i}}{\rho}\right)$

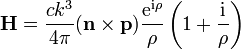
$\mathbf E = \frac{k^3}{4\pi \epsilon_0} \left[ (\mathbf n\times\mathbf p)\times\mathbf n\frac{\mathrm e^{\mathrm i \rho}}{\rho} +\left(3\mathbf n(\mathbf n\mathbf p)-\mathbf p\right) \mathrm e^{\mathrm i \rho}\left(\frac{1}{\rho^3}-\frac{\mathrm i}{\rho^2}\right)\right]$

Im Vakuum strahlt der hertzsche Dipol die mittlere (Strahlungs-)Leistung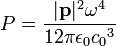

$P = \frac{|\mathbf p|^2 \omega^4}{12 \pi \epsilon_0 {c_0}^3}$

ab, mit:

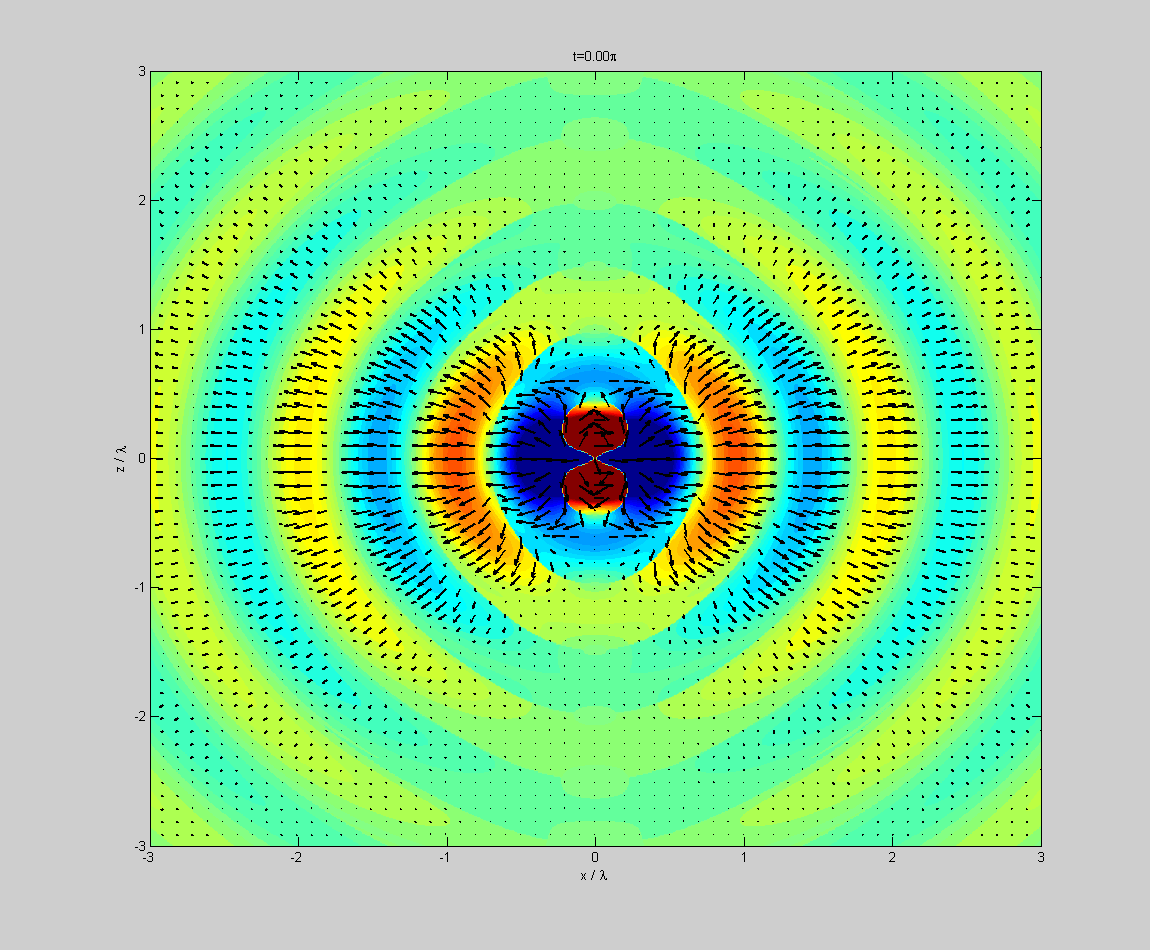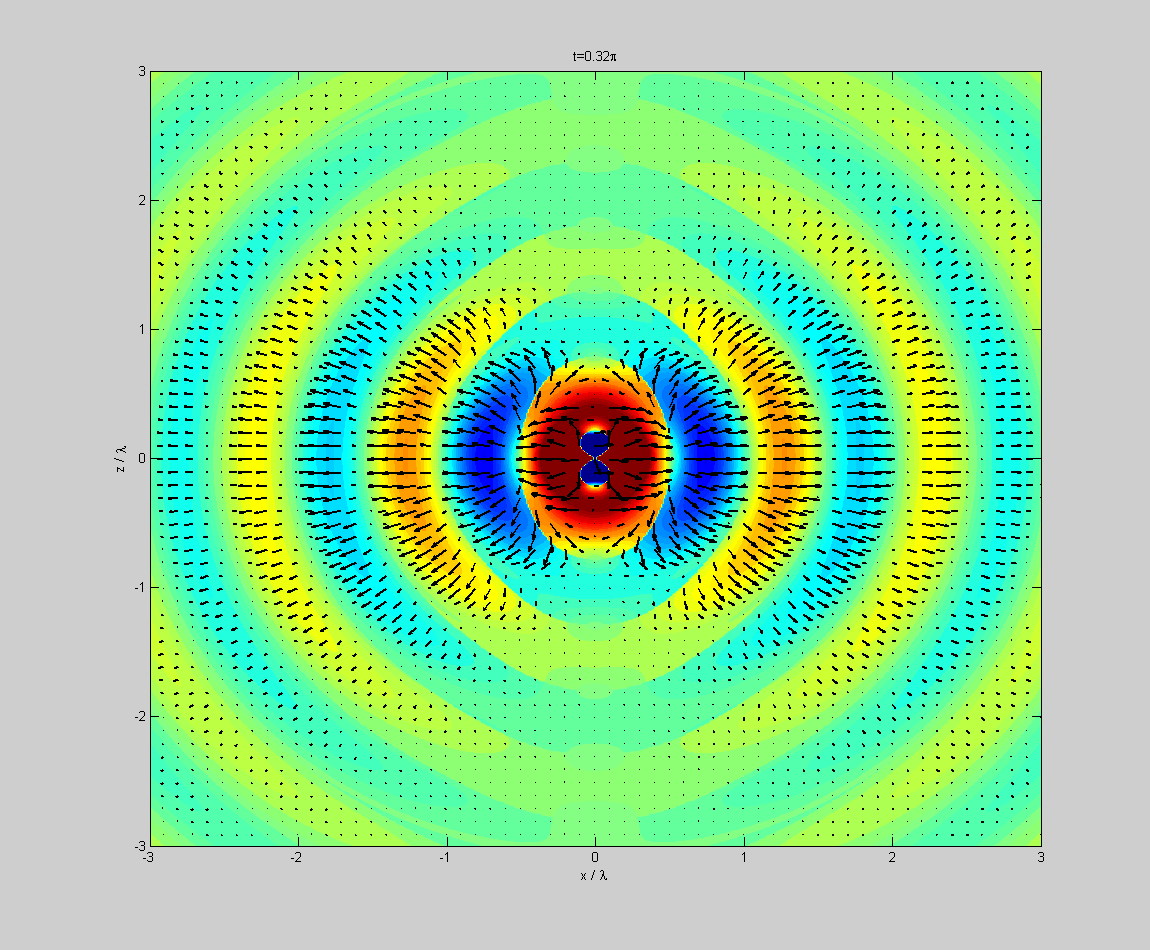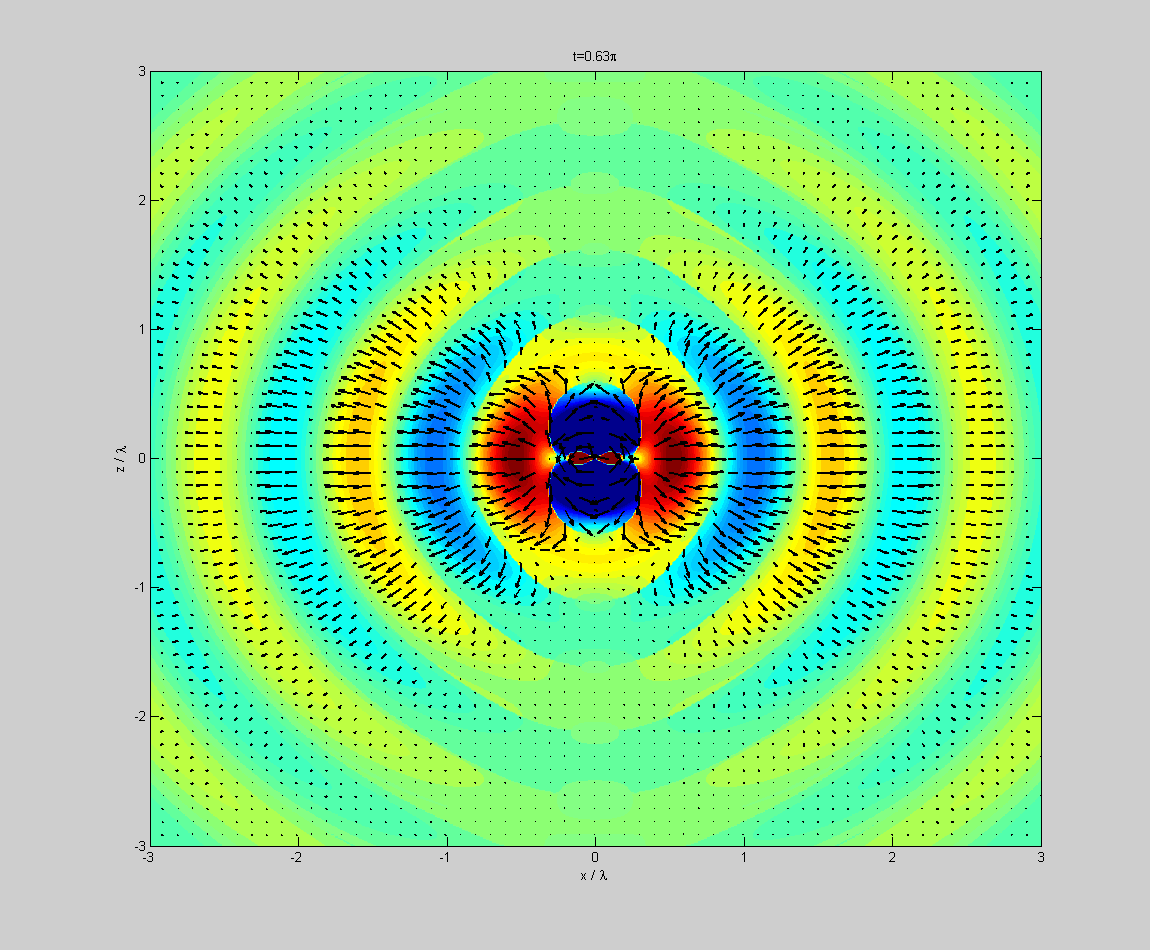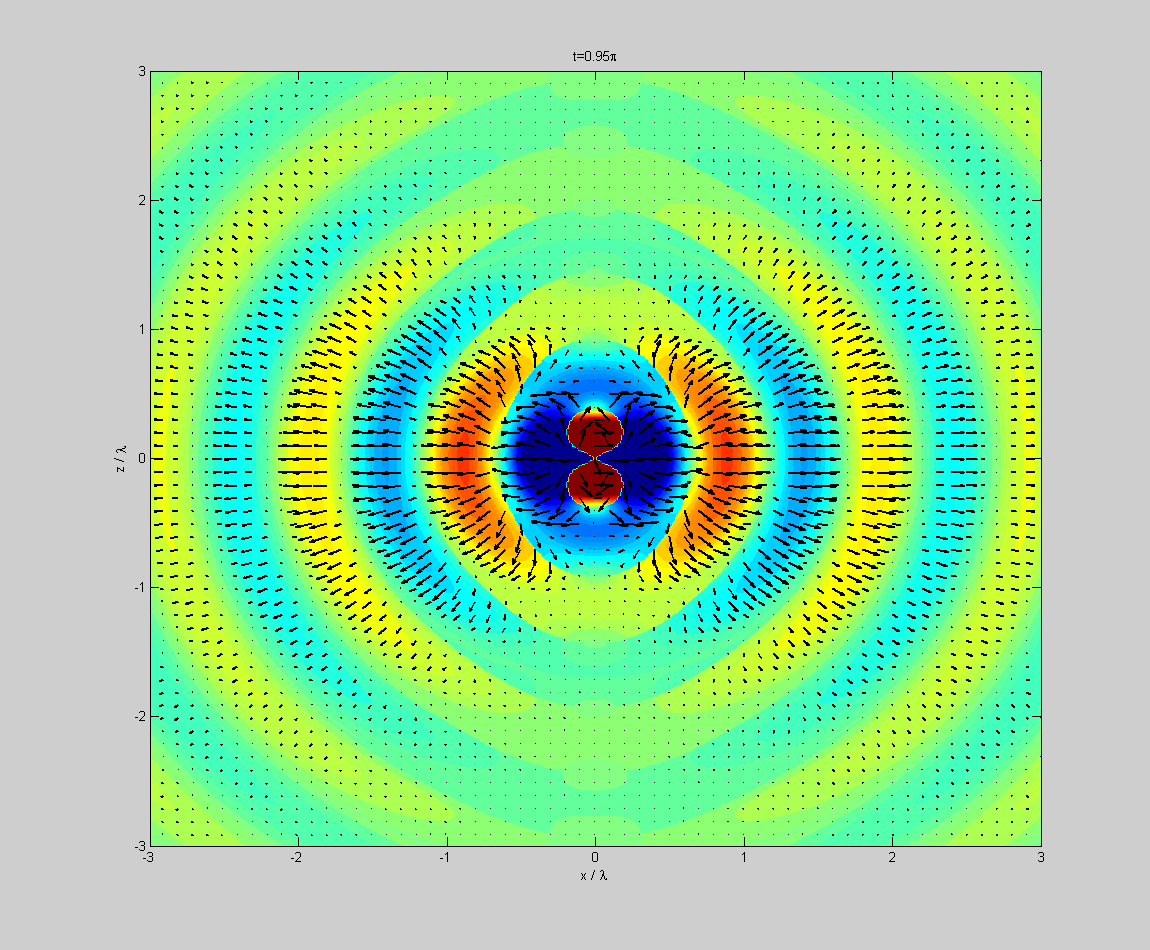Dipolstrahlung. Der Dipol ist parallel zur z-Achse, dargestellt ist die x-z-Ebene. Farbig ist der Betrag der elektrischen Feldstärke 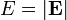$E=|\mathbf E|$, wobei blaue Farben ein nach unten orientiertes elektrisches Feld, und rote Farben ein nach oben orientiertes elektrisches Feld bedeuten. Die schwarzen Pfeile zeigen Richtung und Stärke des Poynting-Vektors an.

• P: mittlere abgestrahlte Leistung
• p: elektrisches Dipolmoment
• ω: Kreisfrequenz der Oszillation
• ε₀: Dielektrizitätskonstante des Vakuums
• c₀: Vakuumlichtgeschwindigkeit.
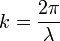• $k=\frac{2\pi}{\lambda}$: Wellenvektor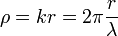
• $\rho=kr =2\pi\frac{r}{\lambda}$

Dabei ist das Internationale Einheitensystem (SI-System, mksA-System) benutzt worden.

Wellen-Ausbreitungsgeschwindigkeiten eines Hertzschen Dipols in Abhängigkeit vom Abstand zur Antenne.

Für den Strahlungswiderstand R_S gilt (Z₀: Freiraumwellenwiderstand, λ: Wellenlänge, L: Antennenlänge):

$R_S = \frac{2 \cdot \pi}{3} \cdot Z_0 \cdot \frac {L}{\lambda^2}$

$\approx 780 \Omega \cdot \frac {L}{\lambda^2}$

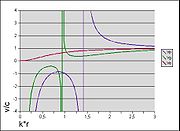
Die Wirkfläche A_W hat die Größe:

$A_W = \frac{3}{8 \cdot \pi} \cdot \lambda^2$

Die Ausbreitungsgeschwindigkeiten der Wellenfronten eines Hertzschen Dipols lassen sich, im Gegensatz zu allen anderen Antennentypen, analytisch berechnen. Das Diagramm rechts zeigt die Abhängigkeit der Phasengeschwindigkeit v_p, der Gruppengeschwindigkeit v_g und der Ausbreitungsgeschwindigkeit der Energie v_e in Einheiten der Lichtgeschwindigkeit c₀ von der Entfernung zur Antenne in Einheiten von 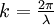$k=\tfrac{2\pi}{\lambda}$. Für große Abstände nähern sich v_g und v_e der Lichtgeschwindigkeit. Im Nahfeld gibt nur v_e die Geschwindigkeit der Signalausbreitung richtig wieder.

Siehe auch

• Dipolantenne

Literatur

• John D. Jackson: Klassische Elektrodynamik. Gruyter, 2002, ISBN 3110165023
• Klaus Kark: Antennen und Strahlungsfelder : elektromagnetische Wellen auf Leitungen, im Freiraum und ihre Abstrahlung mit 79 Tabellen und 125 Übungsaufgaben. Vieweg, Wiesbaden 2006, ISBN 9783834802163