- Hertzscher Dipol
-
Der Hertzsche Dipol (nach Heinrich Hertz), auch Elementardipol genannt, ist die Idealisierung eines elektrischen Strahlers, dient der Berechnung der Abstrahlung realer Antennen sowie als Bezugsantenne, um die Richtwirkung einer Antenne als Gewinn zahlenmäßig zu erfassen.
Inhaltsverzeichnis
Der Hertzsche Dipol als Modell
 Betrag der elektrischen Feldstärke
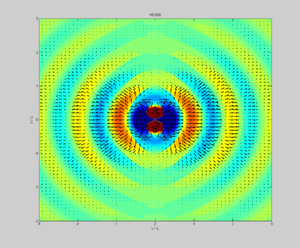
Betrag der elektrischen Feldstärke
 (farbig) und der Poynting-Vektor (schwarze Pfeile) im Nahfeld des vertikal in der Bildebene liegenden Dipols. Blaue/rote Farben bedeuten ein nach unten/oben orientiertes elektrisches Feld.
(farbig) und der Poynting-Vektor (schwarze Pfeile) im Nahfeld des vertikal in der Bildebene liegenden Dipols. Blaue/rote Farben bedeuten ein nach unten/oben orientiertes elektrisches Feld.Dem Hertzschen Dipol als Modell liegt ein sinusförmig (mit Kreisfrequenz ω) variierendes elektrisches Dipolmoment zugrunde, in komplexer Schreibweise
 .
.
Ein solches reines Dipolmoment ohne räumliche Ausdehnung entsteht im Grenzübergang oszillierender Ladungsträger mit verschwindender Schwingungsamplitude und divergierender Ladungsmenge.
Exakte Gleichungen
Für das magnetische und elektrische Feld am durch Abstand r und Richtung
 gegebenen Ort gilt:
gegebenen Ort gilt: (tangential zu Kreisen um die Dipolachse)
(tangential zu Kreisen um die Dipolachse)
![\mathbf E = \frac{\omega^3}{4\pi \epsilon c^3} \left[
(\mathbf n\times\mathbf p)\times\mathbf n\,\frac{1}{\rho}
+\left(3\mathbf n(\mathbf n\mathbf p)-\mathbf p\right)
\left(\frac{1}{\rho^3}-\frac{\mathrm i}{\rho^2}\right)\right]
\,\mathrm{e}^{\mathrm{i} (\rho-\omega t)}](8/b382c97903a5236760a0fa2d857a2226.png) (in Meridionalebenen)
(in Meridionalebenen)
Darin ist
- c die Lichtgeschwindigkeit

 die Permittivität
die Permittivität
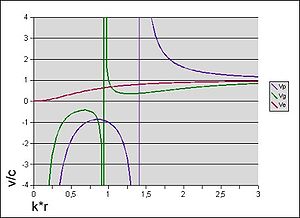
Aus diesen Gleichungen für den Hertzschen Dipol lassen sich, im Gegensatz zu allen anderen Antennentypen, die Ausbreitungsgeschwindigkeiten der Wellenfronten analytisch berechnen. Das Diagramm rechts zeigt die Phasengeschwindigkeit vp, die Gruppengeschwindigkeit vg und die Ausbreitungsgeschwindigkeit der Energie ve in Einheiten der Lichtgeschwindigkeit c als Funktion der Entfernung zur Quelle in Einheiten der Kreis-Wellenzahl
 . Für große Abstände nähern sich alle diese Geschwindigkeiten der Lichtgeschwindigkeit. Im Nahfeld gibt nur ve die Geschwindigkeit der Signalausbreitung richtig wieder.
. Für große Abstände nähern sich alle diese Geschwindigkeiten der Lichtgeschwindigkeit. Im Nahfeld gibt nur ve die Geschwindigkeit der Signalausbreitung richtig wieder.Von der Fernfeldnäherung zum Antennendiagramm
Im Fernfeld sind die Terme mit ρ − 2 und ρ − 3 vernachlässigbar und die Felder entsprechend einfacher:
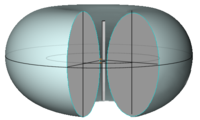 Betrag der Feldstärke im Fernfeld eines vertikalen Hertzschen Dipols in Kugelkoordinaten
Betrag der Feldstärke im Fernfeld eines vertikalen Hertzschen Dipols in Kugelkoordinaten
Der Betrag des gemeinsamen Faktors
 enthält die Richtungsabhängigkeit der Feldstärke. Sie variiert wie
enthält die Richtungsabhängigkeit der Feldstärke. Sie variiert wie  mit dem Winkel φ zur Äquatorebene und ist unabhängig vom Azimut (siehe nebenstehendes Antennendiagramm).
mit dem Winkel φ zur Äquatorebene und ist unabhängig vom Azimut (siehe nebenstehendes Antennendiagramm).
Der Poynting-Vektor gibt die Energieflussdichte an. Sein Betrag, zeitlich gemittelt, ist
gibt die Energieflussdichte an. Sein Betrag, zeitlich gemittelt, istund bis auf den r2-Faktor gleich der Strahlungsintensität
 .
.
Integriert über alle Richtungen ergibt sich die insgesamt abgestrahlte Leistung zu
 ,
,
die isotrop verteilt eine Strahlungsintensität von
ergäbe. Das als Antennengewinn bezeichnete Verhältnis
 beträgt damit also 1,5 (etwa 1,76 dBi).
beträgt damit also 1,5 (etwa 1,76 dBi).Literatur
- John D. Jackson: Klassische Elektrodynamik. Gruyter, 2002, ISBN 3-11-016502-3
- Klaus Kark: Antennen und Strahlungsfelder : elektromagnetische Wellen auf Leitungen, im Freiraum und ihre Abstrahlung mit 79 Tabellen und 125 Übungsaufgaben. Vieweg, Wiesbaden 2006, ISBN 978-3-8348-0216-3
Weblinks
- Berechnungen und Animationen zum Hertz'schen Dipol
Wikimedia Foundation.