- Hauptreihenstern
- Dieser Artikel behandelt den Begriff Hauptreihe im astronomischen Sinn; für Hauptreihe in der Chemie siehe Periodensystem.
- L = 4πσR2T4
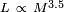
![\begin{smallmatrix} \tau_{ms}\ \sim \ 10^{10} \text{Jahre} \cdot \left[ \frac{M}{M_{\bigodot}} \right] \cdot \left[ \frac{L_{\bigodot}}{L} \right]\ =\ 10^{10} \text{Jahre} \cdot \left[ \frac{M_{\bigodot}}{M} \right]^{2.5} \end{smallmatrix}](/pictures/dewiki/99/cf1e707b281949d6d8cd14b84cb08f23.png)
- ↑ S. Ninkovic und V. Trajkovska: On the mass distribution of stars in the solar neighbourhood. In: Serb. Astron. J.. 172, 2006, S. 17–20 (doi:10.2298/SAJ0672017N).
- ↑ Malcolm S. Longair: The Cosmic Century: A History of Astrophysics and Cosmology (auf Englisch). Cambridge University Press 2006, ISBN 0-521-47436-1
- ↑ a b Laurie M. Brown, Pais, Abraham; Pippard, A. B.: Twentieth Century Physics (auf Englisch). CRC Press 1995, ISBN 0-7503-0310-7
- ↑ a b H. N. Russell: "Giant" and "dwarf" stars. In: The Observatory. 36, 1913, S. 324–329
- ↑ Bengt Strömgren: On the Interpretation of the Hertzsprung-Russell-Diagram. In: Zeitschrift für Astrophysik. 7, 1933, S. 222–248
- ↑ Evry L. Schatzman, Praderie, Francoise: The Stars (auf Englisch). Springer 1993, ISBN 3-540-54196-9
- ↑ W. W. Morgan, Keenan, P. C.; Kellman, E.: An atlas of stellar spectra, with an outline of spectral classification (auf Englisch). Chicago, Illinois: The University of Chicago press 1943
- ↑ a b c Albrecht Unsöld: The New Cosmos (auf Englisch), S. p. 268, Springer-Verlag New York Inc. 1969
- ↑ Origin of the Hertzsprung-Russell Diagram (Englisch). University of Nebraska. Abgerufen am 6. Dezember 2007.
- ↑ George Gloeckler, Geissc, Johannes: Composition of the local interstellar medium as diagnosed with pickup ions. In: Advances in Space Research. 34, Nr. 1, 2004, S. 53–60. doi:10.1016/j.asr.2003.02.054
- ↑ Govert Schilling: New Model Shows Sun Was a Hot Young Star. In: Science. 293, Nr. 5538, 2001, S. 2188–2189. doi:10.1126/science.293.5538.2188. PMID 11567116
- ↑ Zero Age Main Sequence (Englisch). The SAO Encyclopedia of Astronomy. Swinburne University. Abgerufen am 9. Dezember 2007.
- ↑ a b Donald D. Clayton: Principles of Stellar Evolution and Nucleosynthesis (auf Englisch). University of Chicago Press 1983, ISBN 0-226-10953-4
- ↑ Main Sequence Stars (Englisch). Australia Telescope Outreach and Education. Abgerufen am 4. Dezember 2007.
- ↑ Patrick Moore: The Amateur Astronomer (auf Englisch). Springer 2006, ISBN 1-85233-878-4
- ↑ White Dwarf (Englisch). COSMOS—The SAO Encyclopedia of Astronomy. Swinburne University. Abgerufen am 4. Dezember 2007.
- ↑ a b c d Brainerd, Jim (16. Februar, 2005). Main-Sequence Stars (Englisch). The Astrophysics Spectator. Abgerufen am 4. Dezember 2007.
- ↑ a b c Hannu Karttunen: Fundamental Astronomy (auf Englisch). Springer 2003, ISBN 3-540-00179-4
- ↑ M. S. Oey, Clarke, C. J.: Statistical Confirmation of a Stellar Upper Mass Limit. In: The Astrophysical Journal. 620, Nr. 1, 2005, S. L43–L46. doi:10.1086/428396
- ↑ Lawrence H. Aller: Atoms, Stars, and Nebulae (auf Englisch). Cambridge University Press 1991, ISBN 0-521-31040-7
- ↑ Lochner, Jim; Gibb, Meredith; Newman, Phil (6. September, 2006). Stars (Englisch). NASA. Abgerufen am 5. Dezember 2007.
- ↑ D. O. Gough: Solar interior structure and luminosity variations. In: Solar Physics. 74, 1981, S. 21–34. doi:10.1007/BF00151270
- ↑ Thanu Padmanabhan: Theoretical Astrophysics (auf Englisch). Cambridge University Press 2001, ISBN 0-521-56241-4
- ↑ J. T. Wright: Do We Know of Any Maunder Minimum Stars?. In: The Astronomical Journal. 128, Nr. 3, 2004, S. 1273–1278. doi:10.1086/423221
- ↑ Roger John Tayler: The Stars: Their Structure and Evolution (auf Englisch). Cambridge University Press 1994, ISBN 0-521-45885-4
- ↑ I. P. A. Sweet, Roy, A. E.: The structure of rotating stars. In: Monthly Notices of the Royal Astronomical Society. 113, 1953, S. 701–715
- ↑ Burgasser, Adam J.; Kirkpatrick, J. Davy; Lepine, Sebastien (5.-9. Juli, 2004). Spitzer Studies of Ultracool Subdwarfs: Metal-poor Late-type M, L and T Dwarfs (Englisch) S. p. 237. Dordrecht, D. Reidel Publishing Co.. Abgerufen am 6. Dezember 2007.
- ↑ S. F. Green, Jones, Mark Henry; Burnell, S. Jocelyn: An Introduction to the Sun and Stars. Cambridge University Press 2004, ISBN 0-521-54622-2
- ↑ Richmond, Michael (10. November, 2004). Stellar evolution on the main sequence (Englisch). Rochester Institute of Technology. Abgerufen am 3. Dezember 2007.
- ↑ David Arnett: Supernovae and Nucleosynthesis: An Investigation of the History of Matter, from the Big Bang to the Present (auf Englisch). Princeton University Press 1996, ISBN 0-691-01147-8—Hydrogen fusion produces 8×1018 erg/g while helium fusion produces 8×1017 erg/g.
- ↑ Für eine detaillierte historische Rekonstruktion der theoretischen Ableitung dieser Beziehung von Eddington von 1924, siehe:Stefano Lecchini: How Dwarfs Became Giants. The Discovery of the Mass-Luminosity Relation (auf Englisch). Bern Studies in the History and Philosophy of Science 2007, ISBN 3-9522882-6-8
- ↑ Richmond, Michael. Stellar evolution on the main sequence (Englisch). Abgerufen am 24. August 2006.
- ↑ Gregory Laughlin, Bodenheimer, Peter; Adams, Fred C.: The End of the Main Sequence. In: The Astrophysical Journal. 482, 1997, S. 420-432. doi:10.1086/304125
- ↑ Imamura, James N. (7. Februar, 1995). Mass-Luminosity Relationship (Englisch). University of Oregon. Abgerufen am 8. Januar 2007.
- ↑ Donald D. Clayton: Principles of Stellar Evolution and Nucleosynthesis (auf Englisch). University of Chicago Press 1983, ISBN 0-226-10953-4
- ↑ Dina Prialnik: An Introduction to the Theory of Stellar Structure and Evolution (auf Englisch). Cambridge UniversityPress 2000, ISBN 0-521-65937-X
- ↑ Claus E. Rolfs, Rodney, William S.: Cauldrons in the Cosmos: Nuclear Astrophysics (auf Englisch). University of Chicago Press 1988, ISBN 0-226-72457-3
- ↑ Pavel Kroupa: The Initial Mass Function of Stars: Evidence for Uniformity in Variable Systems. In: Science. 295, Nr. 5552, 2002, S. 82–91. doi:10.1126/science.1067524. PMID 11778039
- ↑ Fynbo, Hans O. U. et al: Revised rates for the stellar triple-α process from measurement of 12C nuclear resonances. In: Nature. 433, 2004, S. 136–139. doi:10.1038/nature03219
- ↑ Sitko, Michael L. (24. März, 2000). Stellar Structure and Evolution (Englisch). University of Cincinnati. Abgerufen am 5. Dezember 2007.
- ↑ Staff (12. Oktober, 2006). Post-Main Sequence Stars. Australia Telescope Outreach and Education. Abgerufen am 8. Januar 2008.
- ↑ Lawrence M. Krauss, Chaboyer, Brian: Age Estimates of Globular Clusters in the Milky Way: Constraints on Cosmology. In: Science. 299, Nr. 5603, 2003, S. 65–69. doi:10.1126/science.1075631. PMID 12511641
Der Hauptreihe (meist auch Nullalter-Hauptreihe) werden in der Astronomie die „normalen“ Sterne (Zwergsterne) während der längsten Zeit ihrer Entwicklung zugeordnet.
Inhaltsverzeichnis |
Details
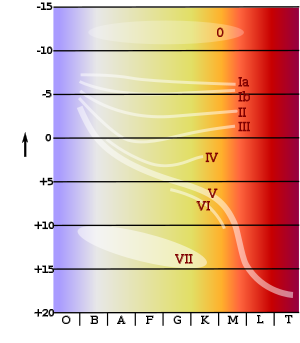
Die Hauptreihe ist ein Bereich im Hertzsprung-Russell-Diagramm, der sich von unten rechts (rot und leuchtkraftarm) nach oben links (blau und hell) erstreckt. Hauptreihensterne werden der Leuchtkraftklasse V zugeordnet. Die Sonne befindet sich im Diagramm nahe der Mitte (im unteren rechten Drittel der Hauptreihe), da sie ein relativ massearmer Stern ist. Ihre Masse wird traditionell auf ungefähr den Durchschnitt der Sterne geschätzt; nach neueren Forschungen liegt sie allerdings deutlich höher, und die Durchschnittsmasse der existierenden Sterne liegt bei ungefähr 0,6 Sonnenmassen.[1]
Diese Reihe ist als solche erkennbar, weil Sterne sich die längste Zeit ihres Lebens (während des Wasserstoffbrennens im Kern) dort aufhalten. Der physikalische Zustand entspricht einem stabilen Gleichgewicht. Durch die Umwandlung von Wasserstoff in Helium verändert sich der chemische Aufbau der Sterne und dadurch die Farbe und die Leuchtkraft, weshalb sie sich innerhalb der Hauptreihe nach oben links bewegen. Die Hauptreihe weist außerdem eine gewisse Dicke auf, da sich die Bahn im HR-Diagramm von zwei Sternen gleicher Masse aufgrund leicht unterschiedlicher Metallizitäten unterscheiden kann.
Erst beim Erlöschen des Wasserstoff-Kernbrennens und dem Einsetzen des Schalenbrennens verlassen die Sterne die Hauptreihe nach rechts und oben und werden zu roten Riesen. Sie können die Hauptreihe jedoch in späteren Stadien durchqueren, wobei sie dabei natürlich nicht mehr die Eigenschaften von typischen Hauptreihensternen annehmen.
Die Hauptreihe kann in einen unteren und einen oberen Bereich geteilt werden. Diese Unterteilung basiert auf den Prozessen, wie in Sternen Energie produziert wird. Sterne unterhalb 1,5 Sonnenmassen verschmelzen Wasserstoffatome zu Helium (Proton-Proton-Reaktion). Oberhalb dieser Masse (in der oberen Hauptreihe) werden in den Kernfusionsprozessen Atome wie Kohlenstoff, Stickstoff und Sauerstoff als Zwischenprodukte für die Produktion von Helium aus Wasserstoffatomen verwendet (Bethe-Weizsäcker-Zyklus).
Durch das Temperaturgefälle zwischen dem Kern des Sterns und seiner Oberfläche wird die erzeugte Energie kontinuierlich durch die dazwischen liegenden Schichten nach außen transportiert, bis sie schließlich in der Photosphäre abgestrahlt wird. Dieser Transport geschieht entweder durch Konvektion oder durch Strahlung und ist abhängig von den lokalen Bedingungen. Energietransport durch Konvektion tritt eher in Regionen mit einer hohen Temperaturdifferenz, einer hohen Opazität oder beiden auf. Wenn Konvektion im Kern auftritt, durchmischt diese dadurch die bisher erzeugte Helium-"Asche" mit frischem Wasserstoff-"Brennstoff", der für die Fusion benötigt wird.
Geschichte
Mit Beginn des zwanzigsten Jahrhunderts konnten mehr Informationen über die Typen und Entfernungen von Sternen erhalten werden. Die Spektren der Sterne zeigten unterschiedliche Eigenheiten, durch welche sie kategorisiert werden konnten. Annie Jump Cannon und Edward Charles Pickering vom Harvard College Observatory hatten eine Methode zur Kategorisierung entwickelt, die als Harvard-Klassifikation bekannt wurde. Dieses Schema wurde in den Harvard Annals 1901 publiziert.[2]
Der dänische Astronom Ejnar Hertzsprung entdeckte 1906 in Potsdam, dass die rötlichsten Sterne – klassifiziert als K und M Sterne im Harvard Schema – in zwei verschiedene Gruppen unterteilt werden können. Diese Sterne sind entweder sehr viel heller als die Sonne oder viel schwächer. Um diese Gruppen zu unterscheiden, nannte er sie „Riesen“ und „Zwerge“. Im folgenden Jahr begann er mit der Untersuchung von Sternhaufen, großen Gruppierungen von Sternen, die alle ungefähr in derselben Entfernung liegen. Er veröffentlichte erste Diagramme, die die Farbe mit der Leuchtkraft dieser Sterne verglichen. Diese Diagramme zeigten eine herausragende, kontinuierliche Reihe von Sternen, die er Hauptreihe nannte.[3]
An der Princeton University verfolgte Henry Norris Russell eine ähnliche Idee. Er untersuchte die Beziehung zwischen der spektralen Klassifikation von Sternen und ihrer absoluten Helligkeit, d.h. der Helligkeit unabhängig von der Entfernung. Zu diesem Zweck benutzte er eine Auswahl von Sternen, die verlässliche Parallaxen haben und die bereits in Harvard kategorisiert wurden. Nachdem er die Spektraltypen dieser Sternen gegen ihre absolute Helligkeit aufgezeichntet hatte, fand er, dass die Zwergsterne einer deutlichen Beziehung folgten. Dies erlaubte es, die wahre Helligkeit eines Zwergsterns mit hinreichender Genauigkeit hervorzusagen.[4]
Bei den roten Sternen, die von Hertzsprung beobachtet wurden, folgten die roten Zwergsterne der Spektal-Leuchtkraft-Beziehung von Russell. Die Riesensterne waren jedoch viel heller als die Zwerge und unterlagen demzufolge nicht der gleichen Beziehung. Russell schlug vor, dass die „Riesensterne eine niedrige Dichte oder eine große Oberflächenleuchtkraft haben müssen, und das Gegenteil gilt für die Zwergsterne.“ Die gleiche Kurve zeigte, dass es sehr wenige weiße schwache Sterne gibt.[4]
1933 führte Bengt Strömgren den Begriff Hertzsprung-Russell-Diagramm ein, um ein Spektral-Leuchtkraft Diagramm zu bezeichnen.[5] Dieser Name spiegelt die parallele Entwicklung dieser Technik von Hertzsprung und Russell Anfang des Jahrhunderts wieder.[3]
Als Entwicklungsmodelle von Sternen während der 1930er Jahre entwickelt wurden, zeigte sich für Sterne mit einheitlicher chemischer Zusammensetzung eine Beziehung zwischen der Masse des Sterns einerseits und seiner Leuchtkraft und seines Radius andererseits. Das heißt, sobald die Masse und Zusammensetzung eines Sterns bekannt ist, kann der Radius und die Leuchtkraft berechnet werden. Diese Beziehung wurde bekannt als das Vogt-Russell-Theorem, benannt nach Heinrich Vogt und Henry Norris Russell. (Im Nachhinein wurde entdeckt, dass dieses Theorem nicht für Sterne mit ungleichmäßiger Zusammensetzung gilt).[6]
Ein verfeinertes Schema für die stellare Einstufung wurde 1943 von W.W. Morgan and P. C. Keenan veröffentlicht.[7] Die MK-Klassifizierung ordnete jedem Stern einen Spektraltyp – basierend auf der Harvard-Klassifikation – und eine Leuchtklasse zu. Die Spektraltypen der Sequenz folgten absteigenden Temperaturen mit Farben von Blau bis Rot. Diese wurden aus historischen Gründen mit O, B, A, F, G, K und M bezeichnet. Die Leuchtkraftklassen reichten von I bis V geordnet nach fallender Leuchtkraft. Sterne der Leuchtkraftklasse V gehörten zur Hauptreihe.[8]
Merkmale
Hauptreihensterne wurden durch Sternmodelle ausgiebig untersucht, so dass ihre Entstehung und Entwicklungsgeschichte relativ gut verstanden sind. Die Position von Sternen auf der Hauptreihe liefert Informationen über ihre physikalischen Eigenschaften.
Die Temperatur eines Sterns kann näherungsweise bestimmt werden, indem man ihn als einen idealen Strahler behandelt, einen Schwarzen Körper. In diesem Fall sind die Leuchtkraft L und der Radius R abhängig von der Temperatur T durch das Stefan-Boltzmann-Gesetz:
wobei σ die Stefan–Boltzmann Konstante ist. Die Temperatur und Zusammensetzung der Photosphäre eines Sterns bestimmt die Energieabstrahlung in unterschiedlichen Wellenlängen. Der Farbindex oder B − V misst die Differenz in diesen Energie-Emissionen mit Hilfe von Filtern, welche die scheinbare Helligkeit des Sterns im blauen (B) und grün-gelben (V) Licht messen. (Durch Messung dieser Differenz entfällt die Notwendigkeit, die Helligkeit anhand der Entfernung zu korrigieren.) Dadurch kann die Position des Sterns im HR-Diagram benutzt werden, den Radius und Temperatur abzuschätzen.[9] Da die Temperatur auch die physikalischen Eigenschaften des Plasmas in der Photosphäre ändert, bestimmt die Temperatur ebenso den Spektraltyp.
Entstehung
Sobald sich ein Protostern aus dem Zusammenbruch einer riesigen molekularen Wolke aus Gas und Staub im lokalen interstellaren Medium bildet, ist seine ursprüngliche Zusammensetzung homogen und besteht aus 70 % Wasserstoff, 28 % Helium und Spuren anderer Elemente.[10] Während dieses ersten Kollapses erzeugt der Vor-Hauptreihenstern Energie durch gravitative Kontraktion. Beim Erreichen einer geeigneten Dichte beginnt im Kern die Energieproduktion durch einen exothermischen Prozess (Kernfusion), bei dem Wasserstoff in Helium umgewandelt wird.[8]
Sobald die Kernfusion von Wasserstoff der beherrschende Energieproduktionsprozess wird und die überschüssige Energie aus der gravitativen Kontraktion verschwunden ist,[11] erreicht der Stern eine Kurve im Hertzsprung-Russell-Diagramm, die Hauptreihe. Astronomen bezeichnen dieses Stadium manchmal als Nullalter-Hauptreihe („Zero age main sequence“, ZAMS).[12] Diese Kurve wurde durch Computermodelle errechnet (ab dem Zeitpunkt, ab dem ein Stern mit der Heliumproduktion beginnt); seine Helligkeit und seine Oberflächentemperatur erhöhen sich üblicherweise mit dem Alter von diesem Zeitpunkt an.[13]
Der Stern bleibt nahe seiner initialen Position in der Hauptreihe, bis etwa 10 Prozent der ursprünglich im Kern vorhandenen Wasserstoffmenge in Helium umgewandelt wurde. Diese Phase ist die längste in einem Sternenleben, da alle weiteren Phasen (das so genannte Heliumbrennen, das Kohlenstoffbrennen und weitere Phasen) sehr viel schneller ablaufen. Ab dann beginnt er sich zu einem leuchtkräftigeren Stern zu entwickeln. (Im HR-Diagramm wandert der sich entwickelnde Stern nach oben und rechts der Hauptreihe). Damit stellt die Hauptreihe das Stadium des primären Wasserstoff-Brennens eines Sternenlebens dar.[8]
Die Mehrheit der Sterne eines typischen HR-Diagramms liegen entlang der Hauptreihen-Linie. Diese Linie ist deshalb so ausgeprägt, weil der Spektraltyp und die Leuchtkraft nur von der Sternmasse abhängen, solange im Kern Wasserstoff fusioniert wird - und dies tun fast alle Sterne die meiste Zeit ihres „aktiven“ Lebens.[14] Die Sterne der Hauptreihe werden Zwergsterne genannt. Dies nicht deshalb, weil sie ungewöhnlich klein wären, sondern weil sie kleinere Durchmesser und weniger leuchtkräftig sind als der andere Haupttypus von Sternen, den Riesen.[15] Weiße Zwerge sind eine andere Sternart, die kleiner sind als die Sterne der Hauptreihe – ungefähr die Größe der Erde. Sie repräsentieren das Endstadium von vielen Sternen der Hauptreihe.[16]
Energieerzeugung

Alle Hauptreihensterne haben eine Kernregion, in der Energie durch Kernfusion erzeugt wird. Die Temperatur und Dichte dieses Kerns sind in dieser Höhe notwendig, um eine Energieproduktion zu unterhalten, um den Rest des Sterns zu stützen. Eine Reduktion der Energieproduktion würde dazu führen, dass sich die darüberliegenden Massen zusammenziehen, und die Temperatur und Druck für die Kernfusion würde wieder erhöht. Ebenso würde eine Erhöhung der Energieproduktion dazu führen, dass der Stern expandiert und der Druck auf den Kern nachlässt. So bildet der Stern ein selbstregulierendes System im hydrostatischen Gleichgewicht, welches während der gesamten Hauptreihenzeit stabil ist.[17]
Astronomen teilen die Hauptreihe in einen oberen und unteren Bereich, basierend auf dem Typ der Fusionsprozesse im Kern. Sterne im oberen Teil der Hauptreihe haben genügend Masse für den CNO-Zyklus, um Wasserstoff in Helium umzuwandeln. Dieser Prozess benutzt Kohlenstoff, Stickstoff und Sauerstoff als Katalysatoren im Fusionsprozess. Im unteren Teil der Hauptreihe entsteht die Energie als Resultat des Proton-Proton-Prozesses, bei dem Wasserstoff direkt in Helium verschmolzen wird.[18]
Ab einer Kerntemperatur von 18 Millionen Kelvin sind beide Fusionsprozesse gleich effizient. Dies ist die Kerntemperatur eines Sterns mit 1,5facher Sonnenmasse. Deshalb besteht der obere Teil der Hauptreihe aus Sternen überhalb dieser Masse. Die obere Massengrenze für Hauptreihensterne ist anscheinend 120–200 Sonnenmassen.[19] Die untere Grenze für eine anhaltende Kernfusion liegt bei etwa 0,08 Sonnenmassen.[18]
Struktur
Siehe auch Sternaufbau
Durch die Temperaturdifferenz zwischen Kern und der Oberfläche wird die Energie nach außen transportiert. Die Energie wird entweder durch Konvektion oder durch Strahlung transportiert. Eine Strahlungszone, in der die Energie durch Strahlung transportiert wird, ist gegen Konvektion stabil und das Plasma wird dort wenig durchmischt. In der Konvektionszone wird die Energie jedoch durch Massentransport von Plasma verteilt, indem heißeres Material aufsteigt und kälteres Material absinkt. Konvektion ist ein effizienterer Modus als Strahlung, um Energie zu transportieren, wird jedoch nur unter Bedingungen auftreten, bei denen ein steiler Temperaturgradient auftritt.[20][17]
In massereichen Sternen ist die Rate der Energieproduktion durch den CNO-Zyklus gegenüber der Temperatur sehr empfindlich, so dass sich die Fusion sehr stark im Kern konzentriert. Folglich besteht ein hohes Temperaturgefälle im Kern, wodurch eine Konvektionszone für einen besseren Energietransport entsteht.[18] Die Vermischung von Material um den Kern entfernt die Helium-Asche der wasserstofferzeugenden Region, wodurch mehr Wasserstoff im Stern verbrannt werden kann. Die äußeren Regionen massereicher Sterne transportieren Energie durch Strahlung ohne Konvektion.[17]
Klasse A-Sterne mittlerer Masse wie Sirius können die Energie vollständig durch Strahlung transportieren.[21] Sterne mit durchschnittlicher Größe und kleiner Masse wie die Sonne haben eine Kernregion, die stabil ist gegen Konvektion, und eine umgebende Konvektionszone nahe der Oberfläche. Dadurch entsteht eine gute Vermischung der äußeren Schichten, aber auch eine weniger effiziente Verbrennung von Wasserstoff im Stern. Das mögliche Resultat ist der Aufbau eines heliumreichen Kerns, der von einer wasserstoffreichen Region umgeben ist. Im Gegensatz hierzu sind kalte und massearme Stern vollständig konvektiv. Das im Kern produzierte Helium wird im ganzen Stern verteilt, dadurch entsteht eine relativ einheitliche Atmosphäre.[17]
Änderungen der Farbe und Helligkeit
Weil sich nicht fusionsfähige Helium-Asche im Kern ansammelt, führt die Verminderung des Wasserstoffs pro Masseeinheit zu einer allmählichen Senkung der Rate der Kernfusion innerhalb dieser Masse. Zum Ausgleich erhöhen sich die Kerntemperatur und Druck langsam, welches eine Erhöhung der Gesamt-Fusionsrate bewirkt. Dies führt zu einer stetigen Zunahme der Leuchtkraft und des Radius des Sterns im Laufe der Zeit.[13] So war zum Beispiel die Leuchtkraft der jungen Sonne nur bei ca. 70 % ihres heutigen Wertes[22] Der Leuchtkraftzuwachs ändert die Position des Sterns im HR-Diagramm was dazu führt, dass sich das Hauptreihenband verbreitert, da die Sterne in unterschiedlichen Stadien ihres Lebens beobachtet werden.[23]
Die Sterne in der Hauptreihe liegen nicht auf einer engen Kurve im HR-Diagramm. Dies liegt hauptsächlich an Beobachtungsungenauigkeiten, die die Entfernungsbestimmung des Sterns beeinflussen, und an der Übernahme von unaufgelösten Doppelsternen. Jedoch würden auch perfekte Beobachtungen zu einer verbreiterten Hauptreihe führen, da die Masse nicht der einzige Parameter eines Sterns ist.
Zusätzlich zu Variationen der chemischen Zusammensetzung – wegen der initialen Häufigkeiten und des Entwicklungsstadiums des Sterns[24] – kann das Vorhandenseins eines nahen Begleitsterns,[25] einer schnellen Rotation[26] oder eines stellaren Magnetfeldes dazu führen, dass sich ein Stern auf der Hauptreihe bewegt, um nur einige Faktoren zu nennen.
Es gibt zum Beispiel Sterne mit einer sehr niedrigen Häufigkeit von Elementen mit höherer Atommasse als Helium – bekannt als metallarme Sterne -, die leicht unterhalb der Hauptreihe liegen. Diese Unterzwerge verschmelzen Wasserstoff in ihrem Kern und markieren so die untere Grenze der verbreiterten Hauptreihe aufgrund der chemischen Zusammensetzung.[27]
Eine fast senkrechte Region des HR-Diagramms ist bekannt als Instabilitätsstreifen und wird besetzt von pulsierenden veränderlichen Sternen. Diese Sterne verändern ihre Helligkeit in regelmäßigen Abständen. Dieser Streifen schneidet die Hauptreihe im oberen Bereich in der Region der Klasse A und F Sterne, mit einer Masse von ein bis zwei Sonnenmassen. Hauptreihensterne in dieser Region erfahren jedoch nur kleine Änderungen in der Helligkeit und sind demzufolge schwierig zu entdecken.[28]
Lebensdauer
Die Lebensdauer, die ein Stern auf der Hauptreihe verbringt, wird bestimmt durch zwei Faktoren. Der Gesamtbetrag der Energie, der durch Kernfusion von Wasserstoff erzeugt werden kann, ist beschränkt durch die Menge an verfügbaren Wasserstoff, der im Kern verarbeitet werden kann. Für einen Stern im Gleichgewicht muss die im Kern erzeugte Energie mindestens gleich sein zu der Energie, die über die Oberfläche abgestrahlt wird. Da sich die Leuchtkraft aus der Menge an Energie, die pro Zeiteinheit ausgestrahlt wird, errechnet, kann die gesamte Lebensdauer in einer ersten Annäherung abgeschätzt werden durch die produzierte Gesamtenergie geteilt durch die Leuchtkraft des Sterns.[29]
Unsere Sonne ist seit ungefähr 4,6 Milliarden Jahren ein Hauptreihenstern und wird es für weitere 6,4 Milliarden Jahre bleiben. Dies ergibt eine gesamte Lebenszeit auf der Hauptreihe von 11×109 Jahren. Nachdem der Wasserstoff im Kern aufgebraucht ist, wird sie expandieren, ein Roter Riese werden und dabei Heliumatome zu Kohlenstoff fusionieren. Weil der Energieausstoß bei der Heliumfusion pro Masseneinheit nur ein Zehntel des Energieausstoßes des Wasserstoff-Prozesses beträgt, wird dieses Stadium nur 10 % der aktiven Lebenszeit des Sterns betragen. Deshalb sind im Durchschnitt etwa 90 % der beobachteten Sterne auf der Hauptreihe.[30]
Im Durchschnitt folgen die Hauptreihensterne einem empirischen Masse-Leuchtkraft-Gesetz.[31] Die Leuchtkraft (L) eines Sterns hängt näherungsweise mit der Gesamtmasse (M) zusammen wie in der folgenden Gleichung:
Die Menge an Brennstoff, der für die Kernfusion verfügbar ist, ist proportional zu der Masse des Sterns. Deshalb kann die Lebensdauer eines Sterns der Hauptreihe geschätzt werden, indem man ihn mit der Sonne vergleicht:[32]
wobei M und L die Masse und die Leuchtkraft des Sterns sind, oder 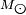 ist eine Sonnenmasse,
ist eine Sonnenmasse, 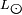 ist die Sonnenleuchtkraft und τms ist die geschätzte Lebenszeit des Sterns auf der Hauptreihe.
ist die Sonnenleuchtkraft und τms ist die geschätzte Lebenszeit des Sterns auf der Hauptreihe.
Dies ist ein unerwartetes Ergebnis, da massereichere Sterne mehr Brennstoff haben und man deswegen annehmen könnte, dass sie länger brennen. Stattdessen leben die leichtesten Sterne mit einer Masse von einem Zehntel der Sonne über eine Billion Jahre.[33] Für die massereichsten Sterne passt diese Masse-Leuchtkraft-Beziehung kaum zur geschätzten Lebensdauer, welche nur einige Millionen Jahre beträgt. Eine genauere Darstellung ergibt eine unterschiedliche Funktion für unterschiedliche Massebereiche.
Die Masse-Leuchtkraft-Beziehung hängt davon ab, wie effizient Energie vom Kern zur Oberfläche transportiert werden kann. Eine höhere Opazität hat eine isolierende Wirkung, so dass mehr Energie im Kern verbleibt. So muss der Stern nicht so viel Energie aufbringen, um im hydrostatischen Gleichgewicht zu verbleiben. Im Gegensatz dazu führt eine niedrigere Opazität dazu, dass Energie schneller entweicht und der Stern mehr Brennstoff verbrauchen muss, um im Gleichgewicht zu bleiben.[34] Zu beachten ist allerdings, dass eine ausreichend hohe Opazität dazu führt, dass der Energietransport über Konvektion geschieht und sich dadurch die Bedingungen ändern, um im Gleichgewicht zu bleiben.[35] In einem massereichen Hauptreihenstern ist die Opazität dominiert durch die Streuung von Elektronen, welche bei steigendem Temperaturen annähernd konstant bleibt. Deshalb erhöht sich die Leuchtkraft nur zur dritten Potenz der Sternenmasse.[36] Für Sterne unterhalb einem Zehntel der Sonnenmasse wird die Opazität abhängig von der Temperatur, so dass sich die Leuchtkraft nahezu zur vierten Potenz der Masse des Sterns verhält.[37] Für sehr massearme Sterne tragen auch Moleküle in der Sternatmosphäre zur Opazität bei. Unterhalb einer halben Sonnenmasse verändert sich die Leuchtkraft zur 2,3 Potenz der Masse, was im Diagramm in einer Abflachung des Graphs resultiert. Diese Verbesserungen sind jedoch weiterhin nur eine Annäherung an die Realität und die Leuchtkraft-Masse-Beziehung kann sich auch abhängig von der Sternzusammensetzung ändern.[38]
Entwicklungswege
Sobald ein Hauptreihenstern in Kern seinen Wasserstoff verbrannt hat, wird durch den Verlust der Energieerzeugung der gravitative Kollaps wieder aufgenommen. Der den Kern umgebenden Wasserstoff erreicht die notwendige Temperatur und den Druck, um zu fusionieren. Dadurch bildet sich eine wasserstoffbrennende Schale um den Heliumkern. Als Folge dieser Änderungen dehnt sich die äußere Hülle aus, die Temperatur sinkt und der Stern verwandelt sich in einen Roten Riesen. Ab diesem Punkt verlässt der Stern die Hauptreihe und erreicht den Riesenast. (Der Weg eines Stern innerhalb des HR-Diagramms wird Entwicklungsweg genannt). Der Heliumkern des Sterns zieht sich weiterhin zusammen, bis er durch den sogenannten degenerierten Elektronendruck aufgehalten wird – einem quantenmechanischen Effekt, welcher einschränkt, in wie weit Materie verdichtet werden kann.
Für Sterne mit mehr als einer halben Sonnenmasse[39] kann der Kern eine Temperatur erreichen, bei der es möglich wird, dass Kohlenstoff aus Helium über den Drei-Alpha-Prozess erzeugt wird.[40][41]
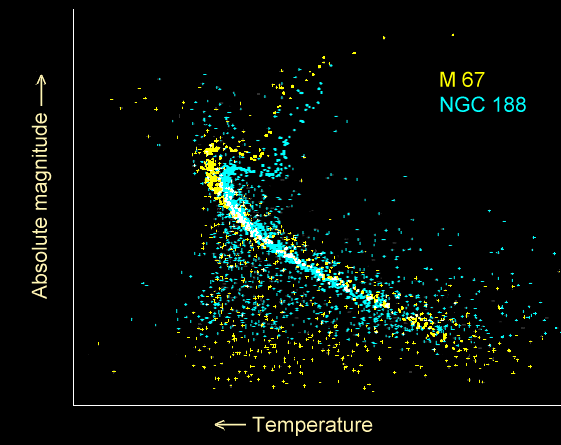
Sobald sich ein Sternhaufen zu einer bestimmten Zeit bildet, hängt die Lebensdauer der Sterne von ihrer individuellen Masse ab. Die massereichsten Sterne werden die Hauptreihe zuerst verlassen, gefolgt von den Sternen mit weniger Masse. Dies geschieht in Abhängigkeit ihrer Position im HR-Diagramm, beginnend auf der linken Seite und sich nach rechts unten fortsetzend. Die Position der Sterne dieses Haufens, welche hier die Hauptreihe verlassen, ist bekannt als Abzweigpunkt. Sobald man die Lebensdauer von Sternen an diesem Punkt der Hauptreihe kennt, kann man das Alter dieses Sternhaufens abschätzen.[42]
Beispiele
| Klasse | Beispielstern | Farbe | Temperatur | Masse | Radius | Leuchtkraft |
|---|---|---|---|---|---|---|
| O | Zeta Ophiuchi | blau | 30.000 K oder mehr | 8 M☉ | 5,4 R☉ | 1.630 L☉ |
| B | Regulus A | blauweiß | 10.000–30.000 K | 3,5 M☉ | 4 R☉ | 150 L☉ |
| A | Zosma | weiß | 7.500–10.000 K | 2,2 M☉ | 2,4 R☉ | 25 L☉ |
| F | Asellus Primus | weißgelb | 6.000–7.500 K | 1,5 M☉ | 1,8 R☉ | 4,4 L☉ |
| G | Sonne | gelb | 5.500–6.000 K | 1 M☉ | 1 R☉ | 1 L☉ |
| K | Epsilon Eridani | orange | 4.000–5.500 K | 0,8 M☉ | 0,8 R☉ | 0,3 L☉ |
| M | Gliese 581 | rot | 2.500–5.500 K | 0,3 M☉ | 0,4 R☉ | 0,002 L☉ |
Siehe auch
Einzelnachweise
Wikimedia Foundation.