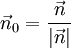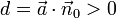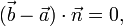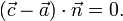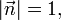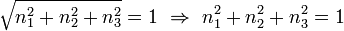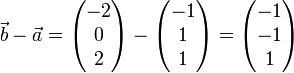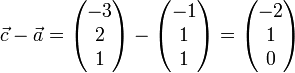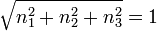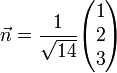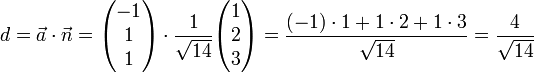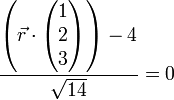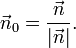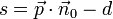Hessische Normalform

Darstellung von Normale und Abstand der hesseschen Normalform

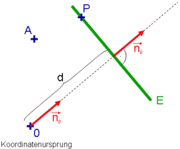
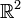Die hessesche Normalform (Hesse-Normalenform), benannt nach Ludwig Otto Hesse, ist in der analytischen Geometrie eine Gleichung, die eine Ebene (E) im euklidischen Raum $\mathbb{R}^3$ oder eine Gerade (g) im $\mathbb{R}^2$ beschreibt und hauptsächlich für Abstandsberechnungen verwendet wird. In vektorieller Schreibweise lautet sie

${\vec r \cdot \vec n_0 - d = 0}$.

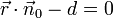Ein Punkt P, der in einem gegebenen Koordinatensystem den Ortsvektor 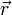$\vec r$ hat, liegt genau dann in der Ebene E (auf der Geraden g), wenn diese Gleichung erfüllt ist.

Dabei steht 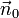$\vec n_0$ für den normierten Normalenvektor (Normaleneinheitsvektor) von E bzw. g, der vom Koordinatenursprung zur Ebene bzw. Geraden zeigt. 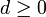$d \ge 0$ ist der Abstand der Ebene (der Geraden) vom Ursprung des Koordinatensystems. Das Multiplikationszeichen $\cdot$ drückt ein Skalarprodukt aus.

Herleitung/Berechnung aus der Normalgleichung

Vorbemerkung: Aus Gründen der Einfachheit ist im Folgenden jeweils von einer Ebene die Rede. Die Überlegungen lassen sich aber auf den Fall einer Geraden übertragen.

In der Normalgleichung

$({\vec r -\vec a)\cdot \vec n = 0}$,

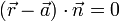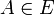ist die Ebene durch einen Normalenvektor $\vec n$ sowie einen beliebigen Ortsvektor $\vec a$ eines Punktes $A \in E$ gegeben. Die Richtung von $\vec n$ sei so gewählt, dass

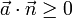$\vec a\cdot \vec n \geq 0$ ist.

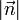Indem man $\vec n$ durch seinen Betrag $| \vec n |$ dividiert, erhält man den normierten Normalenvektor

$\vec n_0 = {{\vec n} \over {| \vec n |}}$

und es gilt

$(\vec r -\vec a)\cdot \vec n_0 = 0$.

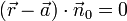Indem man

$d = \vec a\cdot \vec n_0 > 0$

berechnet, erhält man die hessesche Normalform

${\vec r \cdot \vec n_0 - d = 0}$.

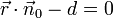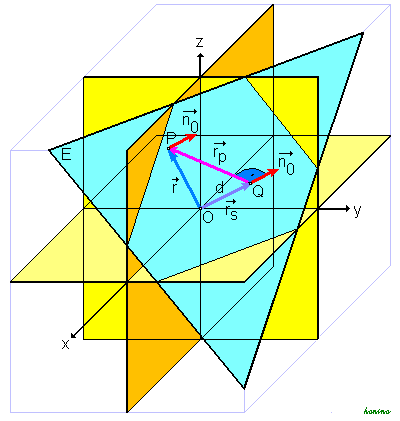
d ist hierin der Abstand vom Ursprung. Da 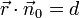$\vec r \cdot \vec n_0 = d$ für jeden Punkt der Ebene gilt, gilt es insbesondere auch für den Punkt Q (Fußpunkt des Lotes vom Ursprung auf die Ebene E) mit 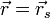$\vec r = \vec r_s$. Dann ist nach Definition des Skalarproduktes

$d = \vec r_s \cdot \vec n_0 = |\vec r_s| \cdot |\vec n_0| \cdot \cos(0^\circ) = |\vec r_s| \cdot 1 = |\vec r_s|$.

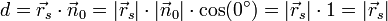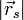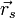Der Betrag $|\vec r_s|$ von ${\vec r_s}$ ist aber der Abstand der Ebene vom Ursprung.

Berechnung aus drei Ortsvektoren über ein Gleichungssystem

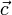Sind die Ortsvektoren $\vec a$, $\vec b$ und $\vec c$ von drei Punkten A, B und C der Ebene gegeben, die nicht auf einer Geraden liegen, und will man daraus die hessesche Normalform berechnen, wertet man die folgenden Gleichungen aus:

$(\vec b - \vec a) \cdot \vec n = 0 ,$

$(\vec c - \vec a) \cdot \vec n = 0 .$

Dieses Gleichungssystem wird erst dadurch eindeutig lösbar, dass man als zusätzliche Bedingung die Normierung

$|\vec n| = 1 ,$

also

$\sqrt{n_1^2 + n_2^2 + n_3^2} = 1\ \Rightarrow \ n_1^2 + n_2^2 + n_3^2 = 1$

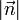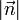verlangt. Einfacher ist es, den übrig behaltenen Freiheitsgrad, nämlich den Betrag (die l₂-Norm) $|\vec n|$ des Vektors $\vec n$ zunächst beliebig zu wählen und dann zu normieren, indem man $\vec n$ durch $|\vec n|$ dividiert.

Beispiel

$\vec a = \begin{pmatrix}-1 \\ 1 \\ 1 \end{pmatrix}; \quad \vec b = \begin{pmatrix}-2 \\ 0 \\ 2 \end{pmatrix}; \quad \vec c = \begin{pmatrix}-3 \\ 2 \\ 1 \end{pmatrix}$.

$\vec b - \vec a = \begin{pmatrix}-2 \\ 0 \\ 2\end{pmatrix} - \begin{pmatrix}-1 \\ 1 \\ 1 \end{pmatrix} = \begin{pmatrix} -1 \\ -1 \\ 1 \end{pmatrix}$

$\vec c - \vec a = \begin{pmatrix}-3 \\ 2 \\ 1 \end{pmatrix} - \begin{pmatrix}-1 \\ 1 \\ 1 \end{pmatrix} = \begin{pmatrix} -2 \\ 1 \\ 0 \end{pmatrix}$

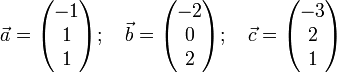Zu lösen ist folgendes Gleichungssystem:

− n₁ − n₂ + n₃ = 0

− 2n₁ + n₂ = 0

$\sqrt{n_1^2 + n_2^2 + n_3^2} = 1$

Lösung:

$\vec n = \frac{1}{\sqrt{14}} \begin{pmatrix}1 \\ 2 \\ 3 \end{pmatrix}$

$d = \vec a \cdot \vec n = \begin{pmatrix}-1 \\ 1 \\ 1 \end{pmatrix} \cdot \frac{1}{\sqrt{14}} \begin{pmatrix}1 \\ 2 \\ 3 \end{pmatrix} = \frac{(-1) \cdot 1 + 1 \cdot 2 + 1 \cdot 3}{\sqrt{14}} = \frac{4}{\sqrt{14}}$

Hessesche Normalform:

$\frac {\left(\vec r \cdot \begin{pmatrix}1 \\ 2 \\ 3 \end{pmatrix}\right) - 4}{\sqrt{14}} = 0$

Berechnung über das Kreuzprodukt

Ein anderer Weg zur Berechnung des Normalenvektors führt über das Kreuzprodukt der beiden Richtungsvektoren. Man erhält in diesem Falle ein eindeutiges Ergebnis

$\vec n = (\vec b - \vec a) \times (\vec c - \vec a)$,

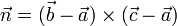wobei man aber auch hier im Allgemeinen $\vec n$ noch normieren muss:

$\vec n_0 = {{\vec n} \over {| \vec n |}} .$

Nun gilt:

• $d = |\vec a| \cdot \cos \phi$
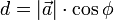
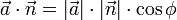• $\vec a \cdot \vec n = |\vec a| \cdot |\vec n| \cdot \cos \phi$ (Definition des Skalarprodukts)
• Da 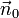$\vec n_0$ auf die Länge 1 normiert ist, kann man schreiben: $\vec a \cdot \vec n_0 = |\vec a| \cdot 1 \cdot \cos \phi = |\vec a| \cdot \cos \phi = d$.

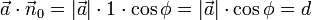Also ergibt sich aus 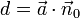$d = \vec a \cdot \vec n_0$ schließlich wieder der Abstand der Ebene zum Nullpunkt. Diese Abstandsberechnung ist ein wichtiges Anwendungsgebiet der hesseschen Normalform.

Anwendung zur Abstandsberechnung

Allgemein erhält man den Abstand s eines beliebigen Punktes P von der Ebene E, indem man den Ortsvektor 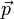$\vec p$ von P für 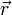$\vec r$ in die linke Seite der hesseschen Normalform einsetzt:

${s = \vec p\cdot \vec n_0 - d}$

Ist s < 0, so liegt P in demselben Halbraum von E wie der Ursprung, bei positivem Vorzeichen von s hingegen im anderen Halbraum.

Verallgemeinerung

Die hessesche Normalform (nicht aber die Berechnung über das Kreuzprodukt) kann man ganz allgemein zur Beschreibung (n-1)-dimensionaler Hyperebenen im n-dimensionalen Raum verwenden.

Siehe auch

• Geradengleichung
• Parameterdarstellung