Hilbert-Schmidt-Klasse

In der Mathematik ist ein Hilbert-Schmidt-Operator (nach David Hilbert und Erhard Schmidt) ein stetiger linearer Operator auf einem Hilbertraum, für den eine gewisse Zahl, die sogenannte Hilbert-Schmidt-Norm, endlich ist. Die Hilbert-Schmidt-Klasse, d. h. die Menge all dieser Operatoren, bildet mit der Hilbert-Schmidt-Norm eine Banachalgebra, die gleichzeitig ein Hilbertraum ist. Hilbert-Schmidt-Operatoren können durch unendlich-dimensionale Matrizen charakterisiert werden.

Motivation

Seien (e_i)_i und (f_i)_i zwei Orthonormalbasen im Hilbertraum H. A sei ein stetiger linearer Operator auf H. Dann gilt

$\sum_i\|Ae_i\|^2 \,=\, \sum_{i,k}|\langle Ae_i,f_k\rangle |^2 \,=\, \sum_{i,k}|\langle e_i,A^*f_k\rangle |^2 \,=\, \sum_k \|A^*f_k\|^2$.

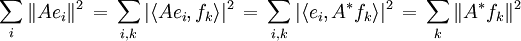Indem man zwei gleiche Orthonormalbasen, 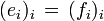$(e_i)_i \,=\, (f_i)_i$, verwendet, zeigt diese Rechnung, dass die linke Seite unverändert bleibt, wenn man A durch A ^* ersetzt. Das gilt dann auch für die rechte Seite. Ersetzt man dort A durch A * bei unterschiedlichen Orthonormalbasen und beachtet A ^{* *} = A, so erkennt man, dass die Größe 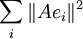$\sum_i\|Ae_i\|^2$ unabhängig von der gewählten Orthonormalbasis ist. Ist diese Größe endlich, so heißt A ein Hilbert-Schmidt-Operator und 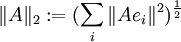$\|A\|_2 := (\sum_i \|Ae_i\|^2)^{\frac{1}{2}}$ ist seine Hilbert-Schmidt-Norm. Statt 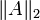$\|A\|_2$ findet man auch die Schreibweise $\|A\|_{HS}$.

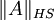Die Hilbert-Schmidt-Klasse, d.h. die Menge aller Hilbert-Schmidt-Operatoren auf H, ist hinsichtlich der algebraischen Operationen Addition, Multiplikation oder Adjunktion abgeschlossen, d.h. sie ist eine Algebra, sie wird mit HS(H) bezeichnet.

Ein Operator 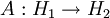$A:H_1\rightarrow H_2$ zwischen zwei Hilberträumen heißt Hilbert-Schmidt-Operator, wenn 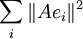$\sum_i\|Ae_i\|^2$ für eine Orthonormalbasis (e_i)_i von H₁ endlich ist. Ähnlich wie oben überlegt man sich, dass diese Zahl von der speziellen Wahl der Orthonormalbasis unabhängig ist, und bezeichnet die Wurzel aus dieser Zahl ebenfalls mit $\|A\|_{HS}$.

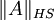Unendliche Matrizen

Legt man eine Orthonormalbasis fest, so kann man jeden stetigen linearen Operator auf H als unendliche Matrix (a_i,j)_i,j mit 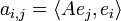$a_{i,j} = \langle Ae_j, e_i\rangle$ auffassen. A ist durch diese Matrix und die gewählte Orthonormalbasis eindeutig bestimmt, denn Ae_i wird auf 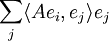$\sum_j \langle Ae_i, e_j\rangle e_j$ abgebildet. Es gilt 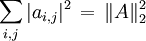$\sum_{i,j}|a_{i,j}|^2 \,=\, \|A\|_2^2$. Daher sind die Hilbert-Schmidt-Operatoren genau diejenigen stetigen, linearen Operatoren, deren Matrixkoeffizienten quadratisch summierbar sind. Mit Hilfe der Hölder-Ungleichung ergibt sich die Submultiplikativität der Hilbert-Schmidt-Norm, d.h. 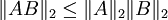$\|AB\|_2 \le \|A\|_2 \|B\|_2$. Die Hilbert-Schmidt-Norm verallgemeinert daher die Frobeniusnorm auf den Fall unendlich-dimensionaler Hilberträume.

HS(H) als Hilbertraum

Das Produkt zweier Hilbert-Schmidt-Operatoren ist stets ein Spurklasse-Operator. Sind A und B zwei Hilbert-Schmidt-Operatoren, so ist daher durch 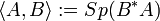$\langle A,B \rangle := Sp(B^*A)$ ein Skalarprodukt auf dem Raum der Hilbert-Schmidt-Operatoren definiert. HS(H) wird mit diesem Skalarprodukt ein Hilbertraum und es ist 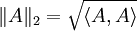$\|A\|_2 = \sqrt{\langle A,A \rangle}$, d.h. die Hilbert-Schmidt-Norm ist eine Hilbertraumnorm.

HS(H) als Banachalgebra

Die Operatoren-Algebra HS(H) ist mit der Hilbert-Schmidt-Norm nicht nur ein Hilbertraum, sondern wegen der Ungleichung 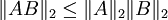$\|AB\|_2 \le \|A\|_2 \|B\|_2$ gleichzeitig eine Banachalgebra. HS(H) ist ein zweiseitiges Ideal in der Algebra B(H) aller stetigen, linearen Operatoren auf H, und es gilt 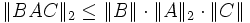$\|BAC\|_2 \le \|B\|\cdot \|A\|_2\cdot \|C\|$ für alle 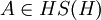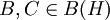$A\in HS(H)$, $B,C \in B(H)$. Jeder Hilbert-Schmidt-Operator ist ein kompakter Operator. Daher ist HS(H) auch ein zweiseitiges Ideal in der C^*-Algebra K(H) der kompakten Operatoren auf H, HS(H) liegt dabei dicht in K(H) bzgl. der Operatornorm. Die Spurklasse N(H) ist als zweiseitiges, dichtes Ideal in HS(H) enthalten. Man hat daher die Inklusionen

$N(H) \subset HS(H) \subset K(H) \subset B(H)$.

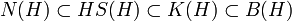Außer {0} und sich selbst enthält HS(H) keine weiteren 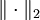$\|\cdot\|_2$-abgeschlossenen zweiseitigen Ideale. Die Algebra der Hilbert-Schmidt-Operatoren ist in diesem Sinne einfach, sie bildet den Grundbaustein der Strukturtheorie der H^*-Algebren.

Literatur

• R.V. Kadison, J. R. Ringrose: Fundamentals of the Theory of Operator Algebras, 1983