- Homomorphie
-
Ein Homomorphismus (aus dem Griechischen, "homós": gleich; "morphé": Form), ist eine strukturerhaltende Abbildung.
Inhaltsverzeichnis
Allgemeine mathematische Definition
Man kann den Homomorphismusbegriff sehr allgemein definieren, in der Kategorientheorie als Morphismus und in der universellen Algebra als Homomorphismus. Die beiden Begriffe unterscheiden sich in einigen Eigenschaften, sind also nicht austauschbar.
Für die bekanntesten algebraischen Strukturen wie Vektorraum, Gruppen, Ringe, Körper sind aber die folgenden Darstellungen einfacher.
Homomorphismen in einigen algebraischen Strukturen
Seien A und B zwei Strukturen, z. B. Gruppen, Vektorräume, Ringe, Körper usw.
Im folgenden bezeichne (A, * 1, * 2,...,e1,e2,...) eine Struktur mit einer Trägermenge A sowie Verknüpfungen * i auf A mit jeweiligen neutralen Elementen ei.
Beispiele sind die Gruppe
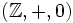 der ganzen Zahlen mit der Addition als Verknüpfung und dem neutralen Element 0 oder der Körper
der ganzen Zahlen mit der Addition als Verknüpfung und dem neutralen Element 0 oder der Körper 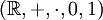 der reellen Zahlen mit der Addition und Multiplikation. Dann gilt folgendes:
der reellen Zahlen mit der Addition und Multiplikation. Dann gilt folgendes:Gruppenhomomorphismus
Eine Abbildung
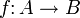 heißt Gruppenhomomorphismus zwischen den Gruppen
heißt Gruppenhomomorphismus zwischen den Gruppen 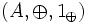 und
und  , wenn für alle
, wenn für alle 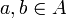 gilt:
gilt: .
.
Damit lässt sich für einen Gruppenhomomorphismus f leicht zeigen, dass
 ,
,
denn es gilt
 . Also ist
. Also ist  das neutrale Element in B.
das neutrale Element in B.
Für alle
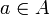 ist
ist  das Inverse zu f(a), d.h.
das Inverse zu f(a), d.h. ,
,
denn es gilt
 .
.
Siehe auch den Artikel Gruppenhomomorphismus.
Ringhomomorphismus
Es seien
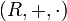 und
und 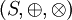 Ringe mit Einselement und
Ringe mit Einselement und 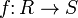 eine Abbildung. f heißt Ringhomomorphismus genau dann, wenn
eine Abbildung. f heißt Ringhomomorphismus genau dann, wenn für alle
für alle 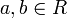 (d.h. f ist ein Gruppenhomomorphismus von
(d.h. f ist ein Gruppenhomomorphismus von 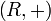 nach
nach 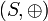 ),
), für alle
für alle 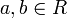 und
und .
.
Wenn x invertierbar ist, dann ist
 .
.Ist
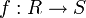 ein Ringhomomorphismus, so ist der Kern von f
ein Ringhomomorphismus, so ist der Kern von fein Ideal in R.
f ist genau dann injektiv, wenn der Kern trivial ist, d. h. nur die Null enthält.
Wenn R ein Körper ist, dann sind {0} und R die einzigen Ideale in R, und damit ist ein Homomorphismus
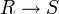 immer injektiv, sofern
immer injektiv, sofern  .
.Körperhomomorphismus
Ein Ringhomomorphismus zwischen zwei Körpern wird auch Körperhomomorphismus genannt.
K-Homomorphismus
Sind L / K und L' / K zwei Körpererweiterungen und ist der Körperhomomorphismus
 eine Fortsetzung der Identität auf K, so nennt man σ einen K-Homomorphismus.
eine Fortsetzung der Identität auf K, so nennt man σ einen K-Homomorphismus.Homomorphismus zwischen Vektorräumen
Homomorphismen von K-Vektorräumen, also Räumen die für die Multiplikation einen Körper K "heranziehen" müssen, sind besser bekannt als lineare Abbildungen. Sie bilden die Grundlage der linearen Algebra.
Weitere Begriffe
universelle Algebra
Ein Homomorphismus f heißt:
- Epimorphismus, wenn f surjektiv ist.
- Monomorphismus, wenn f injektiv ist.
- Isomorphismus, wenn f bijektiv.
- Endomorphismus auf A, wenn
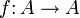 (f bildet A in sich selbst ab).
(f bildet A in sich selbst ab). - Automorphismus auf A, wenn
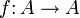 (Endomorphismus) und f bijektiv (Isomorphismus) ist.
(Endomorphismus) und f bijektiv (Isomorphismus) ist.
Kategorientheorie
Ein Homomorphismus f heißt:
- Retraktion, wenn es einen Homomorphismus g gibt, so dass
 ist.
ist. - Schnitt, wenn es einen Homomorphismus g gibt, so dass
 ist.
ist. - Epimorphismus, wenn f rechtskürzbar ist.
- Monomorphismus, wenn f linkskürzbar ist.
- Bimorphismus, wenn f ein Epimorphismus und Monomorphismus ist.
- Isomorphismus, wenn f Retraktion und Schnitt ist.
- Endomorphismus auf A, wenn f von A nach A abbildet.
- Automorphismus auf A, wenn
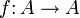 ein Isomorphismus ist.
ein Isomorphismus ist.
Weblinks
Wikimedia Foundation.

