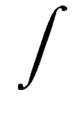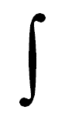Integralzeichen

∫

Das Integralzeichen $\int$ ist aus dem Buchstaben langes s („ſ“) als Abkürzung für das Wort Summe, lateinisch ſumma, entstanden. Prinzipiell ist es ein Teil des Integraloperators. Die symbolische Schreibweise von Integralen geht auf den Mitentdecker der Differential- und Integralrechnung, Gottfried Wilhelm Leibniz, zurück.

Die multiplikativ zu lesende Notation $f(x)\;\mathrm{d}x$ deutet an, wie sich die Integraloperation aus Streifen der Höhe f(x) und der infinitesimalen Breite dx zur Fläche unter der Funktion summiert.

Eine Variante des Integralzeichens ist das Ringintegral (Zirkulation) $\oint$.

Traditionen des Formelsatzes

Das Integralzeichen des amerikanischen Formelsatzes hat sich direkt aus dem »ſ« entwickelt. Im deutschen und russischen Formelsatz hat sich dagegen eine andere Form des Integralzeichens eingebürgert, die im Bild Deutsche Form des Integralzeichens abgebildet ist. Im russischen Raum hat sich zusätzlich noch eine weitere Formvariante etabliert, die die Graphik Russische Formvariante des Integralzeichens wiedergibt.

• 

  Amerikanische Form des Integralzeichens

• 

  Deutsche Form des Integralzeichens

• 

  Russische Formvariante des Integralzeichens

Außerdem schreibt man im amerikanischen Satz in Textformeln die oberen und unteren Grenzen rechts vom Symbol angeordnet^[1], um störende Zeilenabstände einzuschränken,

$\int_0^T f(t)\;\mathrm dt,$

während in deutscher Tradition

$\int\limits_0^T f(t)\;\mathrm dt$

üblich wäre. Auch sind Integrale in Textformeln immer kleiner als in abgesetzten Formeln.

Kodierung

Kodierung mit Unicode, HTML und LaTeX

Zeichen	Unicode Position	Unicode Bezeichnung	Bezeichnung	HTML hexadezimal	HTML dezimal	HTML benannt	LaTeX
∫	U+222B			∫	∫	∫	\int

Es gibt auch Zeichen für doppelte (∬, U+222C), dreifache ( ∭, U+222D) und vierfache Integrale (⨌, U+2A0C), sowie Zirkulationen als Linien- (∮, U+222E), Flächen- (∯ , U+222F) und Volumenintegrale (∰ , U+2230).

Geschichte

„Utile erit scribi ∫ pro omnia.“ (Es wird nützlich sein, ∫ anstatt omnia zu schreiben). Dies vermerkt Gottfried Wilhelm Leibniz 1675 in seiner Abhandlung Analysis tetragonistica. Omnia steht dabei für omnia l und wird in dem geometrisch orientierten Flächenberechnungsverfahren von Bonaventura Cavalieri verwendet. Die zugehörige gedruckte Veröffentlichung Leibniz' ist De geometria recondita von 1686.

Die Mathematikerin Hel Braun sagte einmal:

„Und damit das ganz klar ist: Wenn heutzutage immer wieder Frauen sich benachteiligt fühlen, dann kann ich zwar mitfühlen, aber ich selbst habe mich nie benachteiligt gefühlt. Immer wieder habe ich gesagt, daß die Mathematiker von jedem Frauenzimmer begeistert sind, das ein hübsches Integralzeichen an die Tafel schreiben kann.“

Anmerkungen

1. ↑ In der Wikipedia wird diese Schreibweise angewendet, weil der Formelsatz in der Wikipedia auf TeX basiert, einem amerikanischen System für Text- und Formelsatz