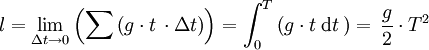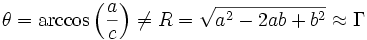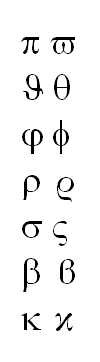- Formelschreibweise
-

DIN 1338 Bereich Schriftverkehr Regelt Formelschreibweise und Formelsatz Kurzbeschreibung regelt die Schreibweise von Formeln im Schriftsatz Letzte Ausgabe 1996-08 ISO - Als Formelsatz bezeichnet man in der Typografie den Satz vor allem mathematischer, aber auch chemischer Formeln, für den Druck oder die Anzeige am Bildschirm. Das Setzen von Formeln ist schwieriger als der Satz von reinem Text, da hierbei Zeichen nicht nur nebeneinander, sondern auch übereinander (z. B. bei Brüchen) gesetzt werden müssen. Manche Zeichen müssen sich über nachfolgende Zeichen erstrecken, wie das Wurzelzeichen, oder ihre Größe abhängig von nachfolgenden Zeichen (z. B. Klammern) oder ihrer Funktion (Indizes und Exponenten) ändern. Eine weitere Schwierigkeit liegt in der Vielfalt der mathematischen Zeichen. Spezielle Zeichen, wie
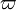 (Lemniskatische Konstante) müssen erkannt und richtig gesetzt werden.
(Lemniskatische Konstante) müssen erkannt und richtig gesetzt werden.Inhaltsverzeichnis
Traditionen des Formelsatzes
In verschiedenen Ländern haben sich im Laufe der Geschichte verschiedene Konventionen für den Satz mathematischer Formeln entwickelt. Sie unterscheiden sich vor allem in den verwendeten Schriftgraden und der Spationierung, also der Verteilung von Leerräumen. Neben diesen kleinen Unterschieden gibt es auch einige große Unterschiede, die im folgenden vorgestellt werden.
Textformeln und abgesetzte Formeln
Im Formelsatz unterscheidet man zwischen im Fließtext stehenden Textformeln wie
![\bar{x}_n = \sqrt[n]{\prod\nolimits_{i=1}^n x_i}](/pictures/dewiki/48/04e3375a8b69ab64d1c8d91dcc41864a.png) und abgesetzten Formeln, die in einer eigenen Zeile stehen, wie
und abgesetzten Formeln, die in einer eigenen Zeile stehen, wieDie beiden Beispiele entsprechen den Konventionen des amerikanischen Formelsatzes. Sie zeigen sich vor allem an der Art, wie obere und untere Grenzen bei Summen- und Produktzeichen gesetzt werden. In Textformeln werden die oberen und unteren Grenzen rechts vom Symbol angeordnet, wie es auch bei Potenzen und Indizes gemacht wird. Dies hat sich eingebürgert, um Platz zu sparen und große Leerräume zwischen den Zeilen wie im folgenden Fall zu vermeiden:
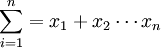 . Diese Leerräume sind für den Verleger ungünstig, weil dadurch sehr viel Papier unbedruckt bleibt, verschlechtern durch die ungleichmäßigen Zeilenabstände die Lesbarkeit und waren im Bleisatz schwierig zu setzen, weil sie vollständig mit Blindmaterial gefüllt werden müssen. Aus demselben Grund wird im angloamerikanischen Raum in Textformeln statt
. Diese Leerräume sind für den Verleger ungünstig, weil dadurch sehr viel Papier unbedruckt bleibt, verschlechtern durch die ungleichmäßigen Zeilenabstände die Lesbarkeit und waren im Bleisatz schwierig zu setzen, weil sie vollständig mit Blindmaterial gefüllt werden müssen. Aus demselben Grund wird im angloamerikanischen Raum in Textformeln statt 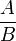 häufig A / B geschrieben.
häufig A / B geschrieben.Bei Integralzeichen werden die Integrationsgrenzen im amerikanischen Formelsatz immer neben das Symbol geschrieben, gleichgültig, ob es in Textformeln oder abgesetzten Formeln steht. In der Wikipedia wird diese Schreibweise angewendet, weil der Formelsatz in der Wikipedia auf TeX basiert, einem amerikanischen System für Text- und Formelsatz. In anderen Traditionen, wie der russischen und auch der deutschen, werden die Grenzen immer, auch beim Integral und in Textformeln, über und unter das Symbol geschrieben, auf das sie sich beziehen. Die obige Formel sähe also in einem deutschen Buch im Fließtext etwa so aus:
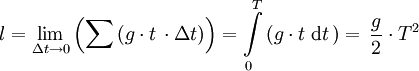
Eine weitere länderspezifische Eigenheit ist der Einsatz verschiedener Schriftgrade. Integrale und Wurzeln sind in Textformeln immer kleiner als in abgesetzten Formeln. Dies geschieht ebenfalls aus oben genannten Gründen der Papierersparnis.
Schriftgrade
Im allgemeinen werden für Indizes und Exponenten kleinere Schriftgrade gewählt als für die eigentlichen Formelbuchstaben. Um wieviel kleiner diese Formelelemente gegenüber dem Rest sind, hängt vom Sprachraum ab. Hier spielen allein schon unterschiedliche Maßsysteme eine Rolle: Amerikanische Drucker verwenden den so genannten Pica-Punkt (auch: Printer's Point), der etwa 0,351 mm misst. Demgegenüber wird in Europa traditionell des französische Punkt-System verwendet wird, das auf François Ambroise Didot zurückgeht. Dieser Didot-Punkt ist etwa 0,376 mm groß und damit größer als der amerikanische Pica-Punkt. Mit der Einführung des Desktop Publishing (DTP) wurde ein weiteres Maß eingeführt, der DTP-Punkt mit der Länge 0,353 mm. Er ist derzeit das einzige verlässliche Maß in den meisten Anwendungsprogrammen, wie etwa Microsoft Word, Photoshop sowie der Druckerkommunikation, während etwa CorelDRAW metrisch programmiert wurde. In LaTeX, und daher auch in der Wikipedia, werden Exponenten und Indizes um 3 pt kleiner als der umgebende Formeltext gesetzt. In Russland dagegen werden Exponenten und Indizes um 2 dd kleiner gesetzt.
Im Formelsatz werden verschiedene Schriftgrößen nicht nur zur Kennzeichnung von Indizes und Exponenten verwendet, auch die Grenzen von Summe, Produkten und Integralen sind in kleinerer Schrift gesetzt. Im amerikanischen Formelsatz werden auch Zähler und Nenner von Brüchen in kleinerer Schrift gesetzt, abhängig davon, wie groß der umgebende Text ist und in welcher Stufe der Bruch steht, wenn es sich um einen mehrfachen Bruch handelt:
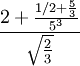 .
.
Im deutschen und russischen Formelsatz dagegen werden zwar Grenzen und Indizes sowie Exponenten kleiner gesetzt, die Nenner und Zähler in Brüchen haben aber immer dieselbe Größe wie im Rest der Formel.
Aussehen mathematischer Symbole
Einige Unterschiede in den unterschiedlichen Traditionen des Formelsatzes betreffen die Form einzelner Zeichen, wie des Wurzel-, Verhältnis- und insbesondere des Integralzeichens, die in angloamerikanischer, deutscher und russischer Tradition unterschiedlich aussehen können.
Amerikanische Form Deutsche Form Russische Form 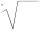
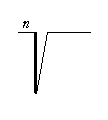
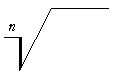
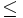
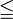
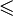
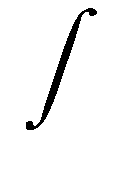
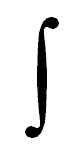
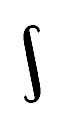
Aufrecht- und Kursivschreibung
Ob Formelbuchstaben, insbesondere griechisch, aufrecht oder kursiv geschrieben werden, hängt ebenfalls stark von der dahinterstehenden Tradition ab.
Allen Traditionen ist es gemein, dass definierte mathematische Funktionen wie sin, exp und ähnliche aufrecht geschrieben werden. Ein Grenzfall ist dabei der Differentialoperator d, der teilweise aufrecht geschrieben wird, da er keine Variable bezeichnet, teilweise kursiv, da er weder Konstante noch Funktion ist.
Im anglo-amerikanischen Sprachraum werden große griechische Buchstaben und Konstanten, wie die Eulersche Zahl e, die imaginäre Einheit i2 = − 1 oder der Goldene Schnitt
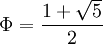 , aufrecht geschrieben, Variablen und kleine griechische Buchstaben dagegen kursiv, beispielsweise
, aufrecht geschrieben, Variablen und kleine griechische Buchstaben dagegen kursiv, beispielsweise 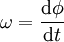 . Im französischen und russischen Formelsatz werden dagegen traditionell alle griechischen Buchstaben sowie zusätzlich im französischen alle Großbuchstaben aufrecht geschrieben. Die Formel
. Im französischen und russischen Formelsatz werden dagegen traditionell alle griechischen Buchstaben sowie zusätzlich im französischen alle Großbuchstaben aufrecht geschrieben. Die Formelnach amerikanischer Tradition wird im russischen Formelsatz mit aufrechtem θ geschrieben:
- θ
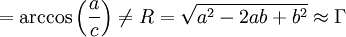 .
.
Im französischen Formelsatz würde neben dem θ auch das R aufrecht geschrieben:
- θ
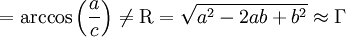 .
.
Im deutschen Formelsatz werden dagegen alle griechischen und lateinischen Buchstaben, kursiv geschrieben, Ausnahmen sind auch hier definierte Funktionsnamen. Die deutsche Variante unterscheidet sich von der amerikanischen nur durch das kursive Γ:
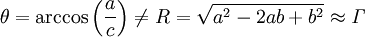 .
.
Eine gewisse Standardisierung hat die ISO-Norm 31 gebracht. Sie schreibt vor, dass mathematische Konstanten wie die Eulersche Zahl oder die imaginäre Einheit aufrecht, Naturkonstanten, wie die Elementarladung
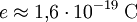 oder die Gravitationskonstante
oder die Gravitationskonstante 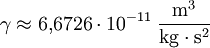 , dagegen kursiv gesetzt werden, weil ihr Wert nur solange gültig ist, bis ein genaueres Messergebnis vorliegt. Variablen werden auch hier stets kursiv geschrieben. Indizes werden abhängig von ihren Eigenschaften groß oder klein geschrieben. Wenn die Indizes den Formelbuchstaben, dem sie zugeordnet sind, beschreiben, etwa TSchmelzpunkt, werden sie aufrecht geschrieben, ansonsten kursiv, z. B.
, dagegen kursiv gesetzt werden, weil ihr Wert nur solange gültig ist, bis ein genaueres Messergebnis vorliegt. Variablen werden auch hier stets kursiv geschrieben. Indizes werden abhängig von ihren Eigenschaften groß oder klein geschrieben. Wenn die Indizes den Formelbuchstaben, dem sie zugeordnet sind, beschreiben, etwa TSchmelzpunkt, werden sie aufrecht geschrieben, ansonsten kursiv, z. B. 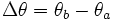 .
.Griechische Buchstaben
Die meisten Formelsatztraditionen verwenden die heute üblichen griechischen Druckbuchstaben. Einige verwenden sie in aufrechter Form, andere schreiben sie kursiv. Eine wichtige Rolle spielt dabei die Form der Kleinbuchstaben (Minuskel): Die beiden Varianten des theta,
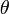 und
und 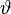 , sind in gedruckten griechischen Texten bedeutungsgleich, in der Mathematik hingegen können diese Zeichen zwei verschiedene Sachverhalte bezeichnen. Ähnliches gilt für
, sind in gedruckten griechischen Texten bedeutungsgleich, in der Mathematik hingegen können diese Zeichen zwei verschiedene Sachverhalte bezeichnen. Ähnliches gilt für 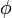 und
und 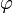 ; hierbei ist zu beachten, dass die erstere Form aus der Handschrift kommt, während letztere die in griechischen Drucken übliche Form darstellt. Beim griechischen Buchstaben Sigma sind die Form σ, die in Drucken am Anfang und in der Mitte eines Wortes auftritt, und die Form
; hierbei ist zu beachten, dass die erstere Form aus der Handschrift kommt, während letztere die in griechischen Drucken übliche Form darstellt. Beim griechischen Buchstaben Sigma sind die Form σ, die in Drucken am Anfang und in der Mitte eines Wortes auftritt, und die Form 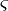 zu unterscheiden, die in Drucktexten am Ende von Worten auftritt. Ein sehr unauffälliger Unterschied liegt beim Epsilon vor:
zu unterscheiden, die in Drucktexten am Ende von Worten auftritt. Ein sehr unauffälliger Unterschied liegt beim Epsilon vor:  im Vergleich zu
im Vergleich zu  . Außerdem werden noch zwei Formen des Kappa und des Beta unterschieden, die auf dem Bild Variantformen griechischer Buchstaben zu sehen sind.
. Außerdem werden noch zwei Formen des Kappa und des Beta unterschieden, die auf dem Bild Variantformen griechischer Buchstaben zu sehen sind.Besonders augenfällig ist der Unterschied bei den beiden Formen des Pi:
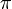 und
und 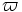 ; die Form
; die Form 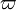 tritt allerdings außerhalb der Astronomie recht selten auf. Beide Formen waren seit dem Mittelalter nebeneinander gebräuchlich,
tritt allerdings außerhalb der Astronomie recht selten auf. Beide Formen waren seit dem Mittelalter nebeneinander gebräuchlich, 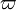 ist sogar noch in einigen griechischen Schreibschriften im 19. Jahrhundert zu finden, seitdem ist es aber aus der normalen griechischen Schrift verschwunden. Heute ist sein Einsatzbereich auf die Mathematik begrenzt.
ist sogar noch in einigen griechischen Schreibschriften im 19. Jahrhundert zu finden, seitdem ist es aber aus der normalen griechischen Schrift verschwunden. Heute ist sein Einsatzbereich auf die Mathematik begrenzt.Welche Formen der griechischen Buchstaben verwendet werden, hängt von der Formelsatztradition ab. Der anglo-amerikanische Formelsatz verwendet alle angegebenen Formen parallel. Im deutschen und russischen Formelsatz hingegen werden außer dem offenen und geschlossenen Theta und den beiden Formen des Sigma keine Variantformen verwendet.
Nach den Empfehlungen der IUPAP sind bis auf
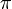 und
und 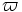 sowie die nichtaustauschbaren Varianten σ und
sowie die nichtaustauschbaren Varianten σ und 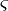 die Variantformen als äquivalent anzusehen und sollen somit keine eigenständige Bedeutung haben.
die Variantformen als äquivalent anzusehen und sollen somit keine eigenständige Bedeutung haben.Zeilenumbruch in Formeln
Lange Formeln können so groß sein, dass sie nicht mehr in eine Zeile passen und auf mehrere Zeilen aufgeteilt werden müssen. Allgemein können Formeln nur an einem Relationszeichen wie dem Gleichheitszeichen oder einem binären Operator getrennt werden, also einem Operator wie dem Plus-Zeichen, das zwischen den beiden Operanden steht. Im russischen Formelsatz wird der Operator am Ende der getrennten Zeile gesetzt und in der neuen Zeile wiederholt, im deutschen und amerikanischen Satz erscheint er dagegen nur in der zweiten Zeile.
Schriftarten für den Formelsatz
In mathematischen Formeln werden Zeichen verwendet, die nur selten in Textschriften vorhanden sind. Dazu zählen zum einen spezielle Verhältniszeichen wie
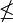 , zum anderen die oben genannten Variantformen griechischer Buchstaben. Um diesem Mangel abzuhelfen, existiert die Schriftart Adobe Symbol, die die griechischen Buchstaben sowie die Variantformen von Theta, Pi und Sigma nebst vieler anderer mathematischer Sonderzeichen wie den wichtigsten Verhältniszeichen, Summenzeichen, Produktzeichen, Integralen und Bausteinen für große Klammern enthält.
, zum anderen die oben genannten Variantformen griechischer Buchstaben. Um diesem Mangel abzuhelfen, existiert die Schriftart Adobe Symbol, die die griechischen Buchstaben sowie die Variantformen von Theta, Pi und Sigma nebst vieler anderer mathematischer Sonderzeichen wie den wichtigsten Verhältniszeichen, Summenzeichen, Produktzeichen, Integralen und Bausteinen für große Klammern enthält.Eine Besonderheit ist die spezifische Form einiger Buchstaben, die sich in Formeln von den Formen in normalem Text unterscheiden. Da in der Mathematik das griechische Ny (ν) verwendet wird, muss sich das lateinische v von diesem unterscheiden. Daher hat das kursive v in Formeln meist die Form eines griechischesn Ypsilon, welches deswegen – ebenso wie das Omikron aufgrund der Ähnlichkeit mit dem o – in der Mathematik nicht verwendet wird. Die Unterschiede sind im nebenstehenden Bild zu sehen. Sie zeigen zunächst ein aufrechtes v und ν sowie darunter zum Vergleich diese Zeichen in den Schriften Times New Roman, Monotype Garamond und Palatino Linotype, um die üblichen Formen dieser Buchstaben zu zeigen. Der mangelnde Unterschied in Times New Roman macht diese Schrift eher ungeeignet für den Formelsatz, ebenso wie viele serifenlose Schriften wie Arial.
Programme für den Formelsatz in elektronischen Medien
Formeleditoren
Ein häufig benutztes Programm für Formelsatz auf dem Computer ist TeX bzw. LaTeX. TeX ist insbesondere im naturwissenschaftlichen Bereich weit verbreitet und setzt sich dort zunehmend als Standard für wissenschaftliche Publikationen durch. Die Gründe dafür liegen neben dem sauberen Layout vor allem auch am hervorragenden Formelsatz.
Bei LaTeX empfiehlt sich die Benutzung der AMS-LaTeX Pakete, die weitere Spezialitäten des Formelsatzes ermöglichen bzw. leichter zugänglich machen. Während beispielsweise beim Setzen von mehrzeiligen Formeln die notbehelfsmässige LaTeX-Umgebung eqnarray den gravierenden typographischen Fehler eines zu großen Leerraumes um das Gleichheitszeichen erzeugt und bei komplexeren Anforderungen an die Ausrichtung untereinander stehender Terme schnell an ihre Grenzen stößt, bietet AMS-LaTeX für diesen Zweck zahlreiche spezialisierte Umgebungen an (z. B. align).
Viele WYSIWYG-Textverarbeitungssysteme stellen für die Eingabe von Formeln so genannte Formeleditoren bereit. Die Eingabe der Formeln mit einem Formeleditor ist zwar intuitiv, aber gleichzeitig etwas umständlich. Die Ausgabequalität lässt oft auch zu wünschen übrig, es sei denn, die Formeleditoren verwenden TeX als Backend. Ein Beispiel eines Formeleditors, der TeX als Backend verwendet, ist das kommerzielle Plugin MathType für MS Word.
Im OpenOffice.org Paket ist die Komponente Math für das Erstellen von Formelsätzen zuständig. In Math erstellte Formelsätze können in Textdokumenten (OOo Writer), Präsentationen (OOo Impress) oder Tabellenkalkulationen (OOo Calc) eingebunden werden. In Math geschriebene Formeln können auch direkt im MathML Format gespeichert werden.
Ein Windows basierter Formeleditor der MathML zur Erzeugung und Einbindung von Formeln als Bild in beliebige Anwendungen erlaubt ist das unter Open Source bereitgestellte Werkzeug "MathCast" (für Windows).
MathML
MathML ist eine Auszeichnungssprache für mathematische Formeln, die vor allem für die Verwendung auf Webseiten gedacht ist. Der Formelsatz in HTML Dokumenten gestaltet sich zur Zeit noch relativ schwierig, da wenige Web-Browser MathML unterstützen. Die zur Zeit gängigste Methode, kompliziertere Formeln auf Webseiten darzustellen, besteht darin, die Formeln mit TeX zu erzeugen und als Grafiken einzubinden. LaTeX2html tut dies automatisch und erstellt gleichzeitig <ALT>-Tags, die den Quellcode der Formel enthalten.
Sonderformen des Formelsatzes
Chemischer Formelsatz
Auch der Satz chemischer Formeln fällt unter den Begriff Formelsatz. In diesem Falle hat der Setzer es zum einen mit den vergleichsweise einfachen Reaktionsgleichungen zu tun, zum anderen mit den deutlich komplexeren Strukturformeln. Reaktionsgleichungen ähneln mathematischen Gleichungen insofern, als auch bei ihnen die Elemente mit hoch-, tief- und übereinandergestellten Symbolen kombiniert werden. Die Ladung eines Ions oder allgemein eines Elementarteilchens wird durch eine hochgestellte Zahl ausgedrückt, die rechts neben dem Element- bzw. Teilchensymbol steht. Die Anzahl der in einem Molekül vorkommenden Atome eines bestimmten Elements wird durch eine tiefgestellte Zahl rechtsseitig des Elementsymbols repräsentiert. Die Oxidationszahl eines Atoms wird durch eine übergestellte römische oder seltener arabische Zahl wiedergegeben. Die Kernladungszahl, also die Anzahl der Protonen im Atomkern, die die Atomsorte bestimmt, wird links unten, die Massenzahl, also die Anzahl aller Teilchen im Atomkern, links oben vom Elementsymbol geschrieben. Diese Elemente chemischer Formeln sind mit den üblichen Mechanismen des mathematischen Formelsatzes, sei es mit Computerprogrammen oder mit Bleilettern, zu realisieren.
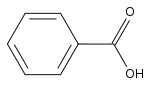
Doch im chemischen Satz tritt noch eine andere Art des Satzes auf: das Setzen chemischer Strukturformeln. Das Setzen chemischer Strukturformeln, ein Beispiel ist im Bild Strukturformel der Benzoesäure wiedergegeben, stellt Satzprogramme, erst recht aber Bleisetzer vor eine große Herausforderung. In Satzprogrammen kann meist zu diesem Zweck eine Graphik gezeichnet werden, in LaTeX etwa mit der picture-Umgebung. Im Bleisatz dagegen muss der Setzer sich vorher ein genaues Bild vom Ergebnis machen, das er wünscht, um die waagerechten, senkrechten und in diversen Winkeln diagonalen Linien zusammen mit den Elementsymbolen richtig anzuordnen. In älteren Büchern, die mit Blei- oder frühem Photosatz gedruckt sind, sieht man daher auch manchmal einen kleinen Zwischenraum zwischen den Linien, die die chemischen Bindungen repräsentieren, welche Zeugnis von den Problemen der komplexen Aufgabe des Satzes chemischer Strukturformeln ablegen.
In Computerprogrammen wird man sich bei einigen wenigen Strukturformeln mit Graphiken behelfen können. Sobald aber mehr als nur ein paar Strukturen auftauchen, die womöglich auch noch sehr komplex sind, ist es meist nötig, einen Zusatz für chemische Formeln zu verwenden. Diese greifen meist auf vorgefertigte Strukturen zurück, in die die Elementsymbole nur eingfügt werden müssen. Für unübliche Strukturen aber ist es nötig, die Formeln logisch zu beschreiben. Ein Beispiel für solch eine Lösung stellt die Pakete XyMTeX [1] und PPCH-TeX dar.
Geschichte
Der Formelsatz ist fast so alt wie der Buchdruck selbst. Den ersten gedruckten Büchern wie der Gutenbergbibel folgten bald auch mathematische Werke. Bis zu Beginn des 19. Jh. war die Qualität des Formelsatzes bescheiden. Ab etwa 1850 verbesserte er sich um 1900 einen vorläufigen Höhepunkt zu erlagen.
Durch die starke Verbreitung der Schreibmaschine ab etwa 1925 trat ein Rückschritt ein: viele mathematische Texte (insbesondere Diplomarbeiten und Dissertationen) wurden nicht mehr in Druckereien professionell gesetzt, sondern selbst vom Autor mit einer Schreibmaschine. Formeln wurden anfangs per Hand in freigelassene Lücken nachgetragen, ab den 1960er Jahren gab es auch spezielle Schreibmaschinen mit halbzeiligem Abstand für Hoch- und Tiefstellungen wodurch einfache Formeln prinzipiell setzbar waren. Auf diese Weise sind eine ganze Reihe von Büchern mit dem charakteristischen Schreibmaschinen-Schriftbild und Flatterrand entstanden (Beispiel: Hans Opolka, Winfried Scharlau: Von Fermat bis Minkowski. 1980).
Dieser Entwicklung hat Donald Knuth ab 1977 mit der Entwicklung von TeX Einhalt geboten. Ab etwa 1994 gilt es als schlechter Stil, mathematische Texte nicht mit TeX zu setzen. Andererseits gab es parallel zum Schreibmaschinensatz in den 1960er Jahren einen zweiten Höhepunkt in der Qualität des Handsatzes (Beispiel: Oskar Perron: Irrationalzahlen. 1960).
Mit dem Formelsatz beschäftigte sich bis zur Einführung von TeX im wesentlichen die Berufsgruppe der Formelsetzer:
„Die Ausbildung im Satz mathematischer und chemischer Formeln ist in den Ausbildungsunterlagen für Schriftsetzer vorgesehen; doch besteht noch vielfach die Meinung, daß diese Satzart nur wenigen Spezialsetzern vorbehalten sei. Deshalb wird hierauf bei der allgemeinen Ausbildung des Setzer meist nur geringer Wert gelegt, und so kommt es, daß der Berufsnachwuchs nur weniger Betriebe den Aufgaben gewachsen ist, die die […] wesentlich steigende Produktion mathematischer und chemischer Bücher an die Schriftsetzereien stellt.“
– P. Fritzsche und H. Wunderlich, 1952
Normen
- DIN 1338 Formelschreibweise und Formelsatz
- DIN 1302 Allgemeine mathematische Zeichen und Begriffe
- DIN 1304 Formelzeichen
- ISO 31 Größen und Einheiten (Quantities and Units)
Siehe auch
Zum Formelsatz in der Wikipedia siehe: Wikipedia:TeX
Literatur
Formelsatz wird in der Literatur selten im Detail behandelt. Die meisten Werke zur Typografie lassen den Formelsatz aus. Gute Informationen zum Formelsatz lassen sich in den folgenden Werken finden:
- Friedrich Forssman, Ralf de Jong: Detailtypografie – Nachschlagewerk für alle Fragen zu Schrift und Satz. 2. Auflage. Hermann Schmidt, Mainz 2005, ISBN 3-87439-642-8
- Jörg Knappen: Schnell ans Ziel mit LATEX 2e. 2. Auflage. Oldenbourg, München 2004, ISBN 3-486-27447-3
- Donald E. Knuth: The TeXbook (Computers and Typesetting Volume A). Addison-Wesley, Reading/Mass. 1984, ISBN 0-201-13448-9
- Paul Fritzsche, Herbert Wunderlich: Der Formelsatz in Mathematik, Chemie und Technik. Mit zahlreichen Ausschließbeispielen. Fachbuchverlag Leipzig, 1952
- Romeo Thieme: Satz und Bedeutung mathematischer Formeln. Bildungsverb. d. Deutschen Buchdrucker, Berlin 1934
Weblinks
- Michael J. Downes: Short Math Guide for LaTeX (PDF 392 KB, englisch).
- Russische typographische Traditionen im mathematischen Formelsatz (PDF 196 KB, englisch).
- Nath, ein LaTeX-Paket zur Verbesserung mathematischen Formelsatzes nach anglo-amerikanischer Tradition (PDF 144 KB, englisch).
Einzelnachweise
- ↑ englischsprachiger Artikel zum Thema XyMTeX
Wikimedia Foundation.