- Jordan-Maß
-
Das Jordan-Maß ist ein Begriff aus der Maßtheorie. Dieser geht auf Marie Ennemond Camille Jordan zurück, welcher ihn im Jahr 1890 aufbauend auf Arbeiten von Giuseppe Peano entwickelte. Mit dem Jordan-Maß kann man beschränkten Teilmengen des
 einen Inhalt zuordnen und erhält einen Integralbegriff, der dem riemannschen Integralbegriff analog ist.
einen Inhalt zuordnen und erhält einen Integralbegriff, der dem riemannschen Integralbegriff analog ist.Inhaltsverzeichnis
Definition
Seien
und
Sei μn den Würfelinhalt, welcher für alle
 mit
mit  durch
durchund
 definiert ist.
definiert ist.Der innere Inhalt einer beschränkten Menge A sei
ihr äußerer Inhalt sei
Eine Menge
 heißt Jordan-messbar, wenn A beschränkt ist und
heißt Jordan-messbar, wenn A beschränkt ist und  .
.Das Jordan-Maß einer Jordan-messbaren Menge A ist durch
 gegeben.
gegeben.Gilt
 für ein beschränktes
für ein beschränktes  , so ist A Jordan-messbar und wird Jordan-Nullmenge genannt.
, so ist A Jordan-messbar und wird Jordan-Nullmenge genannt.Eigenschaften
- Das Jordan-Maß ist ein Inhalt und nicht σ-additiv, d.h. abzählbare Vereinigungen von Jordan-messbaren Mengen müssen nicht notwendig Jordan-messbar sein. (Siehe auch Beispiel 2.) Daher ist das Jordan-Maß kein Maß im Sinne der Maßtheorie.
- Ist
 Jordan-messbar, so ist A auch Lebesgue-messbar, und es gilt λn(A) = in(A). Dabei bezeichnet λn(A) das Lebesgue-Maß von A.
Jordan-messbar, so ist A auch Lebesgue-messbar, und es gilt λn(A) = in(A). Dabei bezeichnet λn(A) das Lebesgue-Maß von A. - Eine Menge
 ist genau dann Jordan-messbar, wenn A beschränkt ist und der Rand von A eine Jordan-Nullmenge ist.
ist genau dann Jordan-messbar, wenn A beschränkt ist und der Rand von A eine Jordan-Nullmenge ist. - Eine beschränkte Menge
 ist genau dann Jordan-messbar, wenn
ist genau dann Jordan-messbar, wenn  ist. Dann gilt auch
ist. Dann gilt auch  .
. - Eine kompakte Menge
 ist genau dann eine Lebesgue-Nullmenge, wenn A eine Jordan-Nullmenge ist.
ist genau dann eine Lebesgue-Nullmenge, wenn A eine Jordan-Nullmenge ist.
Beispiele
- Der Einheitskreis im
 ist Jordan-messbar, da er beschränkt und sein Rand eine Jordan-Nullmenge ist.
ist Jordan-messbar, da er beschränkt und sein Rand eine Jordan-Nullmenge ist. - Die Menge
![A=[0,1]\cap \Q](4/de499417ca81461c28e65766f577b04c.png) ist nicht Jordan-messbar. Denn für jede Menge
ist nicht Jordan-messbar. Denn für jede Menge  gilt
gilt  und für jede Menge
und für jede Menge  gilt
gilt ![[0,1] \subset N,](8/db8e5331375d84a010f23c16b4b37a80.png) woraus
woraus  folgt. Für jedes
folgt. Für jedes  gilt λ1({q}) = i1({q}) = 0. Aufgrund der σ-Additivität des Lebesgue-Maßes gilt
gilt λ1({q}) = i1({q}) = 0. Aufgrund der σ-Additivität des Lebesgue-Maßes gilt  . A ist also Lebesgue-Nullmenge. Das Jordan-Maß ist, wie dieses Beispiel zeigt, nicht σ-additiv.
. A ist also Lebesgue-Nullmenge. Das Jordan-Maß ist, wie dieses Beispiel zeigt, nicht σ-additiv.
Literatur
- Wolfgang Walter: Analysis. 2. Band. 2. Auflage. Springer, Berlin u. a. 1991, ISBN 3-540-54566-2, S. 224–226 (Grundwissen Mathematik 4).
Weblinks
- Jordaninhalt und quadrierbare Mengen
- Quadrierbare Mengen im MitschriebWiki (PDF-Datei; 188 kB)
Wikimedia Foundation.

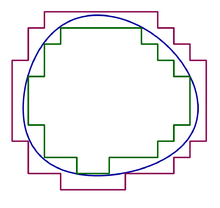
 (mit blauem Rand) wird einmal durch Teilmengen (wie die Menge mit grünem Rand) und einmal durch Obermengen (wie die Menge mit lila Rand) aus
(mit blauem Rand) wird einmal durch Teilmengen (wie die Menge mit grünem Rand) und einmal durch Obermengen (wie die Menge mit lila Rand) aus  angenähert.
angenähert.![J^n := \{ ]a,b[ : a,b \in \R^n , a \leq b \}](1/461ac984f4e58fb0346f8d6f2781387a.png)

![\mu^n\left(]a,b[\right) = \prod_{j=1}^n(b_j - a_j)](e/0be0a1197877a6c2678564e704ac5165.png)

